Python
Graphes et matrices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiches de cours Python
Retrouvez toutes les fiches de cours téléchargeables au format pdf en cliquant sur les liens suivants :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Transposition de matrice
→
→
→
Compléter la fonctions suivante qui prend en argument une matrice \text{M} et qui retourne sa transposée.
→
→
Compléter la fonctions suivante qui prend en argument une matrice \text{M} et qui retourne sa transposée.
def transpose(M):
T = []
for i in range(...):
ligne = []
for j in range(...):
ligne.append(...)
T.append(ligne)
return T
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Matrices symétriques et antisymétriques
→
→
→
1. Compléter la fonction symétrique qui prend en argument une matrice carrée et qui retourne True si elle est égale à sa transposée et False sinon.
2. Écrire une fonction antisymétrique qui retourne True si la matrice est opposée à sa transposée et False sinon.
→
→
1. Compléter la fonction symétrique qui prend en argument une matrice carrée et qui retourne True si elle est égale à sa transposée et False sinon.
2. Écrire une fonction antisymétrique qui retourne True si la matrice est opposée à sa transposée et False sinon.
def symetrique(M):
for i in range(len(M)):
for j in range(len(M)):
if ...
return False
return True
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Produit et puissance de matrice
→
→
→
1. Compléter la fonction mult qui prend en argument deux matrices carrées de même dimension \text{A} et \text{B} et qui retourne la matrice \text{AB}.
2. En déduire la fonction puissance qui prend en paramètre une matrice carrée ainsi qu'un nombre entier n>1 et qui renvoie la matrice \text{A}^n.
→
→
1. Compléter la fonction mult qui prend en argument deux matrices carrées de même dimension \text{A} et \text{B} et qui retourne la matrice \text{AB}.
2. En déduire la fonction puissance qui prend en paramètre une matrice carrée ainsi qu'un nombre entier n>1 et qui renvoie la matrice \text{A}^n.
def mult(A, B):
produit = []
for i in range(len(A)):
ligne = []
for j in range(len(B)):
p = 0
for k in range(len(A)):
p = ...
ligne.append(p)
produit.append(ligne)
return produit
def puissance(A, n):
An = A
for i in range(2, n):
An = ...
return An
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Matrices nilpotentes
→
→
→
→
1. En utilisant la fonction puissance écrite à l'exercice précédent, proposer une fonction nilpotente permettant de tester si une matrice carrée \text{A} ayant n lignes et n colonnes est nilpotente. Cette fonction prendra en argument une matrice carrée n \times n et retournera True si la matrice est nilpotente et False sinon
2. Tester ce programme avec la matrice \text{A}=\begin{pmatrix} 0 & 1 & 1 \\
0& 0& 3 \\
0 & 0 & 0\end{pmatrix}.
→
→
→
1. En utilisant la fonction puissance écrite à l'exercice précédent, proposer une fonction nilpotente permettant de tester si une matrice carrée \text{A} ayant n lignes et n colonnes est nilpotente. Cette fonction prendra en argument une matrice carrée n \times n et retournera True si la matrice est nilpotente et False sinon
Aide
Pour créer la matrice carrée de même taille contenant uniquement des 0, on pourra utiliser la ligne de code zero = [[0]*len(A) for i in range(len(A))]
def comparaison(A,B):
out = True
for i in range(len(A)):
for j in range(len(B)):
if A[i][j]!=B[i][j]:
out = False
return out
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Matrices idempotentes
→
→
→
→
On dit qu'une matrice carrée est idempotente lorsqu'elle est égale à l'une de ses puissances. On admet que si une telle puissance existe, elle est inférieure ou égale à l'ordre de la matrice.
En reprenant et en modifiant le programme de l'exercice précédent, proposer une fonction idempotente qui prend en argument une matrice carrée et qui renvoie True si cette matrice est idempotente et False sinon.
→
→
→
On dit qu'une matrice carrée est idempotente lorsqu'elle est égale à l'une de ses puissances. On admet que si une telle puissance existe, elle est inférieure ou égale à l'ordre de la matrice.
En reprenant et en modifiant le programme de l'exercice précédent, proposer une fonction idempotente qui prend en argument une matrice carrée et qui renvoie True si cette matrice est idempotente et False sinon.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Matrices auto-inverses
→
→
→
→
On dit qu'une matrice carrée \text{A} inversible est auto-inverse si, et seulement si, elle est égale à son propre inverse.
1. Montrer qu'une matrice auto-inverse est idempotente.
2. Écrire en Python un programme prenant en argument un entier naturel non nul n et retournant la matrice identité d'ordre n.
3. Compléter la fonction autoinverse qui prend en paramètre une matrice carrée et qui retourne True si elle est auto-inverse et False sinon.
→
→
→
On dit qu'une matrice carrée \text{A} inversible est auto-inverse si, et seulement si, elle est égale à son propre inverse.
1. Montrer qu'une matrice auto-inverse est idempotente.
2. Écrire en Python un programme prenant en argument un entier naturel non nul n et retournant la matrice identité d'ordre n.
3. Compléter la fonction autoinverse qui prend en paramètre une matrice carrée et qui retourne True si elle est auto-inverse et False sinon.
help
On pourra se servir de la fonction mult des exercices précédents.
def autoinverse(M): return mult(M, M) == ...
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Diviseurs
→
→
→
→
On considère le graphe non orienté dont les sommets sont les nombres entiers de 1 à 60 et construit de la manière suivante : ses sommets sont reliés par une arête si, et seulement si, l'un des deux nombres est divisible par l'autre.
Ainsi, les sommets 2 et 12 sont adjacents, mais pas les sommets 5 et 13.
1. Compléter le programme ci-après afin qu'il affiche le nombre d'arêtes de ce graphe.
2. On considère le graphe similaire d'ordre \text{N} \in \mathbb{N}^*.
Écrire un programme Python prenant en argument l'entier \text{N} et retournant le nombre d'arêtes de ce graphe.
3. On rappelle que tout entier est un diviseur de lui-même. Modifier le programme de la question précédente afin qu'il ne prenne en compte que les diviseurs stricts de chacun des nombres.
→
→
→
On considère le graphe non orienté dont les sommets sont les nombres entiers de 1 à 60 et construit de la manière suivante : ses sommets sont reliés par une arête si, et seulement si, l'un des deux nombres est divisible par l'autre.
Ainsi, les sommets 2 et 12 sont adjacents, mais pas les sommets 5 et 13.
1. Compléter le programme ci-après afin qu'il affiche le nombre d'arêtes de ce graphe.
2. On considère le graphe similaire d'ordre \text{N} \in \mathbb{N}^*.
Écrire un programme Python prenant en argument l'entier \text{N} et retournant le nombre d'arêtes de ce graphe.
3. On rappelle que tout entier est un diviseur de lui-même. Modifier le programme de la question précédente afin qu'il ne prenne en compte que les diviseurs stricts de chacun des nombres.
arete = 0
for i in range(1, 61):
for j in range(...):
if ... :
arete = arete + 1
print(arete)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Degré des sommets d'un graphe
→
→
→
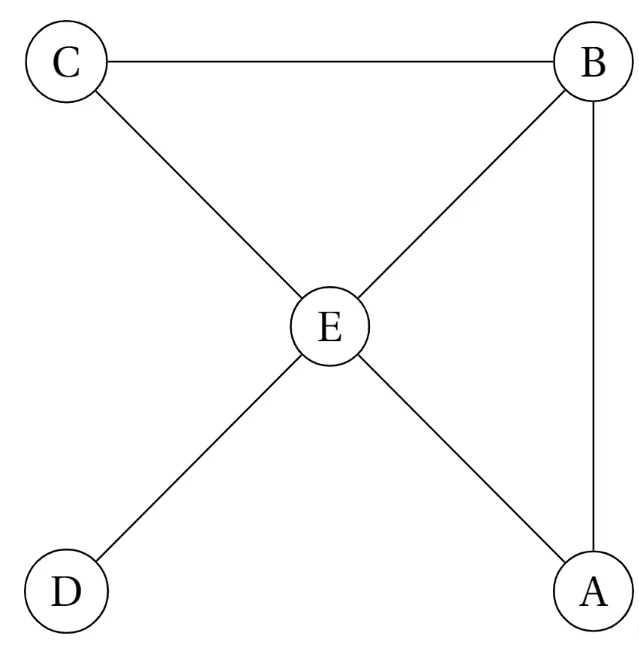
Soit \text{M} la matrice d'adjacence d'un graphe dont les sommets sont des lettres de l'alphabet, les sommets étant rangés dans l'ordre alphabétique.
L'objectif de cet exercice est de classer les sommets par ordre décroissant du degré.
1. Compléter la fonction degres ci-dessous pour qu'elle retourne la liste des degrés de chaque sommet de la matrice d'adjacence \text{M}.
2. À partir de la fonction tri donnée dans l'énoncé, classer les sommets du graphe ci-dessous par ordre décroissant de leur degré.

→
→
Soit \text{M} la matrice d'adjacence d'un graphe dont les sommets sont des lettres de l'alphabet, les sommets étant rangés dans l'ordre alphabétique.
L'objectif de cet exercice est de classer les sommets par ordre décroissant du degré.
1. Compléter la fonction degres ci-dessous pour qu'elle retourne la liste des degrés de chaque sommet de la matrice d'adjacence \text{M}.
2. À partir de la fonction tri donnée dans l'énoncé, classer les sommets du graphe ci-dessous par ordre décroissant de leur degré.


def degres(M):
n = len(M)
degre = n*[0]
for i in range(n):
for j in range(n):
degre[i] = ...
return degre
def tri(sommets, degre):
ordre = len(sommets)
liste_sommets_tries = []
for k in range(ordre):
maximum = max(degre)
index = degre.index(maximum)
degre.pop(index)
sommet_correspondant = sommets[index]
liste_sommets_tries.extend(sommet_correspondant)
sommets.pop(index)
return liste_sommets_tries
sommets = ['A','B','C','D','E']
M = [[0,1,0,0,1],[1,0,1,0,1],[0,1,0,0,1],[0,0,0,0,1],[1,1,1,1,0]]
degre_des_sommets = degres(M)
print(degre_des_sommets)
print(tri(sommets,degre_des_sommets))
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Déterminer le nombre d'arêtes manquantes pour qu'un graphe soit complet
→
→
→
→
On considère un graphe non orienté \text{G} et sans boucle modélisé par sa matrice d'adjacence \text{M}.
1. Énoncer une méthode pour déterminer, à partir de sa matrice d'adjacence, le nombre d'arêtes manquantes pour que le graphe soit complet.
2. Répondre au problème à l'aide d'une fonction Python.
3. Tester le programme avec la matrice \begin{pmatrix} 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 \\0 & 1 & 0 & 0 & 1 \\0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{pmatrix}.
→
→
→
On considère un graphe non orienté \text{G} et sans boucle modélisé par sa matrice d'adjacence \text{M}.
1. Énoncer une méthode pour déterminer, à partir de sa matrice d'adjacence, le nombre d'arêtes manquantes pour que le graphe soit complet.
2. Répondre au problème à l'aide d'une fonction Python.
3. Tester le programme avec la matrice \begin{pmatrix} 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 & 1 \\0 & 1 & 0 & 0 & 1 \\0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \end{pmatrix}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Sommet connecté
→
→
→
→
Écrire une fonction Python qui prend en argument la matrice d'adjacence \text{M} d'un graphe et qui retourne True si au moins un des sommets est adjacent à tous les autres et False sinon.
→
→
→
Écrire une fonction Python qui prend en argument la matrice d'adjacence \text{M} d'un graphe et qui retourne True si au moins un des sommets est adjacent à tous les autres et False sinon.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Voisin de voisins
→
→
→
→
La fonction ci-dessous prend en argument la matrice d'adjacence \text{M} d'un graphe et retourne True si deux sommets ont toujours un sommet adjacent commun et False sinon. Compléter le code afin qu'il réponde à ces exigences.
→
→
→
La fonction ci-dessous prend en argument la matrice d'adjacence \text{M} d'un graphe et retourne True si deux sommets ont toujours un sommet adjacent commun et False sinon. Compléter le code afin qu'il réponde à ces exigences.
def sommets_proches(M):
n = len(M)
out = ...
for i in range(n):
for j in range(i+1, n):
sommets_i_j_connectes = ...
for k in range(n):
if (M[i][k] == 1 and M[j][k] == 1):
sommets_i_j_connectes = ...
if (sommets_i_j_connectes == ...):
out = ...
return out
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Vecteur propre et valeur propre
→
→
→
→
On dit qu'un vecteur non nul \overrightarrow{v} est un vecteur propre d'une matrice \text{A} lorsqu'il existe un nombre réel \lambda tel que \text{A} \overrightarrow{v}=\lambda\overrightarrow{v}.
1. Vérifier que la fonction test_vecteur_propre ci-dessous, qui prend en argument une matrice carrée A de taille 3 et un vecteur \overrightarrow{v} de taille 3, retourne True si le vecteur v est un vecteur propre de \text{A} et False sinon.
2. Tester le programme avec la matrice \text{A} = \begin{pmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{pmatrix} et \overrightarrow{v} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}.
3. Généraliser la fonction ci-dessous à une matrice carrée et un vecteur de taille n quelconque.
→
→
→
On dit qu'un vecteur non nul \overrightarrow{v} est un vecteur propre d'une matrice \text{A} lorsqu'il existe un nombre réel \lambda tel que \text{A} \overrightarrow{v}=\lambda\overrightarrow{v}.
1. Vérifier que la fonction test_vecteur_propre ci-dessous, qui prend en argument une matrice carrée A de taille 3 et un vecteur \overrightarrow{v} de taille 3, retourne True si le vecteur v est un vecteur propre de \text{A} et False sinon.
Aide
Un vecteur est une matrice colonne \begin{pmatrix} x \\
y\\
z\end{pmatrix} qui s'écrit [[x],[y],[z]] en Python.
2. Tester le programme avec la matrice \text{A} = \begin{pmatrix} 2 & -1 & -1 \\ -1 & 2 & -1 \\ -1 & -1 & 2 \end{pmatrix} et \overrightarrow{v} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}.
3. Généraliser la fonction ci-dessous à une matrice carrée et un vecteur de taille n quelconque.
def mult(A,B):
nbLignesA = len(A)
nbColonnesA = len(A[0])
nbColonnesB = len(B[0])
produit = []
for i in range(nbLignesA):
ligne=[]
for j in range(nbColonnesB):
p=0
for k in range(nbColonnesA):
p= p + A[i][k]*B[k][j]
ligne.append(p)
produit.append(ligne)
return produit
def test_vecteur_propre(A, v):
Av = mult(A, v)
produit_en_croix_0 = Av[1][0]*v[2][0] - Av[2][0]*v[1][0]
produit_en_croix_1 = Av[0][0]*v[2][0] - Av[2][0]*v[0][0]
produit_en_croix_2 = Av[0][0]*v[1][0] - Av[1][0]*v[0][0]
if produit_en_croix_0 == 0 and produit_en_croix_1 == 0 and produit_en_croix_2 == 0:
return True
else:
return False
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Suite de matrices
→
→
→
→
Soient k un entier naturel non nul, \text{A} une matrice carrée de taille k, \text{B} une matrice colonne à k lignes et (\text{U}_n) la suite de matrices colonnes définie par son premier terme \text{U}_0 et, pour tout entier naturel n, \text{U}_{n+1} = \text{A}\text{U}_n + \text{B}.
Écrire une fonction suite en Python qui prend en argument les matrices \text{A}, \text{B}, \text{U}_0 et n et qui retourne la matrice \text{U}_n.
→
→
→
Soient k un entier naturel non nul, \text{A} une matrice carrée de taille k, \text{B} une matrice colonne à k lignes et (\text{U}_n) la suite de matrices colonnes définie par son premier terme \text{U}_0 et, pour tout entier naturel n, \text{U}_{n+1} = \text{A}\text{U}_n + \text{B}.
Écrire une fonction suite en Python qui prend en argument les matrices \text{A}, \text{B}, \text{U}_0 et n et qui retourne la matrice \text{U}_n.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
