Ce chapitre permet d'aborder le repérage et des notions vectorielles dans l'espace.

Un drone est un aéronef sans passager pouvant voler de façon autonome ou être contrôlé à distance depuis le sol. Son usage peut être civil ou au profit de forces armées.
Les déplacements d'un drone peuvent être modélisés par des vecteurs.

Caractéristiques d'un vecteur

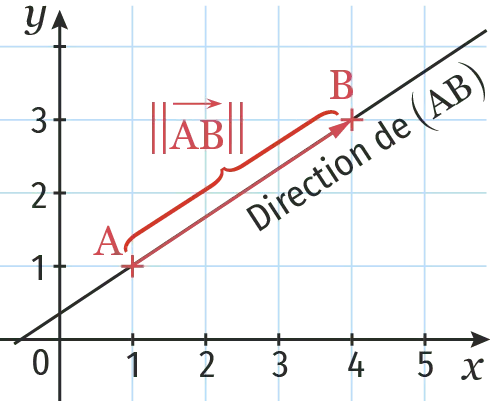
Les caractéristiques d'un vecteur \overrightarrow{\mathrm{AB}} sont :

• sa direction : la droite (\text{AB}) ;
• son sens : de \text{A} vers \text{B} ;
• sa norme notée \|\overrightarrow{\mathrm{AB}}\| : la mesure de la longueur \text{AB}.

Coordonnées et norme d'un vecteur du plan

Dans un repère orthonormé, si \mathrm{A}\left(x_{\mathrm{A}} ; y_{\mathrm{A}}\right) et \mathrm{B}\left(x_{\mathrm{B}} ; y_{\mathrm{B}}\right), alors :

• les coordonnées du vecteur \overrightarrow{\mathrm{AB}} sont \overrightarrow{\mathrm{AB}}\left(\begin{array}{l} x_{\mathrm{B}}-x_{\mathrm{A}} \\ y_{\mathrm{B}}-y_{\mathrm{A}} \end{array}\right) ;
• la norme du vecteur \overrightarrow{\mathrm{AB}} s'obtient de la manière suivante : \|\overrightarrow{\mathrm{AB}}\|=\sqrt{\left(x_{\mathrm{B}}-x_{\mathrm{A}}\right)^{2}+\left(y_{\mathrm{B}}-y_{\mathrm{A}}\right)^{2}} ;

Exemple : Dans le repère ci-dessous, \overrightarrow{\mathrm{AB}}\left(\begin{array}{l} 4-1 \\ 3-1 \end{array}\right), c'est-à-dire \overrightarrow{\mathrm{AB}}\left(\begin{array}{l} 3 \\ 2 \end{array}\right).
De plus, \|\overrightarrow{\mathrm{AB}}\|=\sqrt{(4-1)^{2}+(3-1)^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}.

Particularités

• Deux vecteurs sont dits égaux s'ils ont la même direction, le même sens et la même norme.
• Deux vecteurs sont dits opposés s'ils ont la même direction, la même norme mais sont de sens opposés.
• Deux vecteurs sont dits colinéaires s'ils ont la même direction (mais pas forcément le même sens ni la même norme).

On se place dans la configuration ci-dessous.


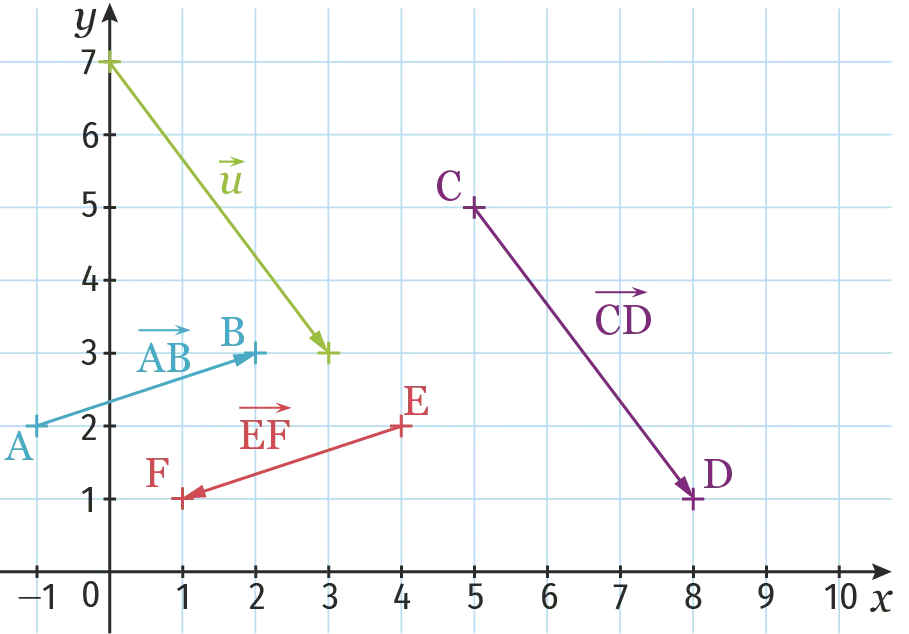
1. Les coordonnées du point \text{A} sont :

a. (-1 \: ; 2)

b. (2 \: ; 3)

c. (2 \: ;-1)

2. Les coordonnées du vecteur \overrightarrow{\mathrm{AB}} sont :

a. \left(\begin{array}{l} 1 \\ 3 \end{array}\right)

b. \left(\begin{array}{l} 3 \\ 1 \end{array}\right)

c. \left(\begin{array}{l} -4 \\ 1 \end{array}\right)

3. La norme \|\overrightarrow{\mathrm{AB}}\| est égale à :

a. \sqrt{10}

b. 10

c. 5

4. Les coordonnées du vecteur \overrightarrow{\mathrm{EF}} sont :

a. \left(\begin{array}{l} 1 \\ 4 \end{array}\right)

b. \left(\begin{array}{l} -3 \\ -1 \end{array}\right)

c. \left(\begin{array}{l} 3 \\ -1 \end{array}\right)

5. Choisir les bonnes réponses.

a. \vec{u}=\overrightarrow{\mathrm{CD}}

b. \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{EF}} sont opposés.

c. \overrightarrow{\mathrm{AB}} et \overrightarrow{\mathrm{EF}} sont colinéaires.

d. \overrightarrow{\mathrm{u}} et \overrightarrow{\mathrm{CD}} sont opposés.