Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 8
Activité A
Étude d'une onde sinusoïdale du type \text{A} \sin(\omega t + \varphi)
Capacité : Connaître les fonctions du type \text{A} \sin(\omega t + \varphi).
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
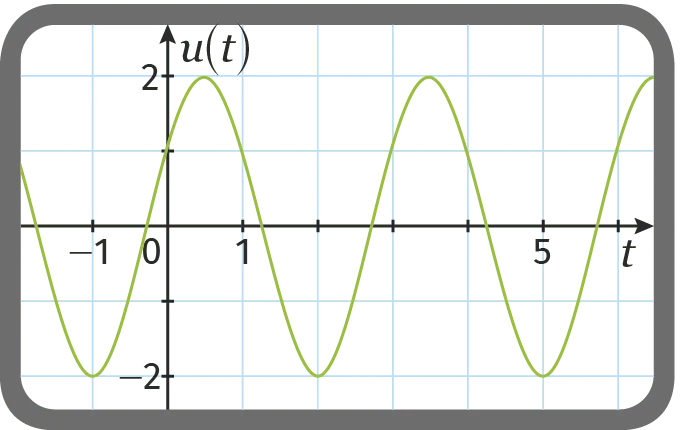
À l'aide d'un oscilloscope, on peut visualiser ci‑après la tension sinusoïdale, en volt, délivrée par un générateur de basses fréquences (GBF) au cours du temps, en seconde. Après une courte étude de son installation, un technicien donne l'expression algébrique de cette fonction : {u(t)=2 \sin \left(\frac{2 \pi}{3} t+\frac{\pi}{6}\right)}
Le zoom est accessible dans la version Premium.
Problématique
Problématique : Quelles sont les différentes grandeurs qui composent cette fonction ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
a.
Réaliser
Repérer les points \text{A}, \text{B} et \text{C} d'abscisses respectives 1, 4 et 7 appartenant à la courbe.
b. Analyser/Raisonner
Que remarque‑t‑on ? Le démontrer par le calcul.
Repérer les points \text{A}, \text{B} et \text{C} d'abscisses respectives 1, 4 et 7 appartenant à la courbe.
b. Analyser/Raisonner
Que remarque‑t‑on ? Le démontrer par le calcul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Analyser/Raisonner
Aide
La fréquence, en hertz, est donnée par la formule \frac{1}{\mathrm{T}}, où \text{T} est la période du signal en seconde.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
a.
S'approprier
Télécharger le fichier GeoGebra où est représentée la fonction f définie par f(t)=\mathrm{A} \sin (\omega t+\varphi). Faire varier les curseurs \text{A}, \omega et \varphi pour observer le changement d'allure de la courbe.
b. Analyser/Raisonner, Communiquer
Décrire l'influence de chacune des grandeurs \text{A}, \omega et \varphi sur la courbe représentative de f.
Dans une fonction du type \textrm{A} \sin(\omega t + \varphi), \text{A} représente l'amplitude, \omega représente la pulsation et \varphi représente la phase à l'origine.
Télécharger le fichier GeoGebra où est représentée la fonction f définie par f(t)=\mathrm{A} \sin (\omega t+\varphi). Faire varier les curseurs \text{A}, \omega et \varphi pour observer le changement d'allure de la courbe.
GeoGebra
b. Analyser/Raisonner, Communiquer
Décrire l'influence de chacune des grandeurs \text{A}, \omega et \varphi sur la courbe représentative de f.
Dans une fonction du type \textrm{A} \sin(\omega t + \varphi), \text{A} représente l'amplitude, \omega représente la pulsation et \varphi représente la phase à l'origine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
a.
Analyser/Raisonner
Afficher, sur le fichier GeoGebra, la fonction u donnée dans l'énoncé.
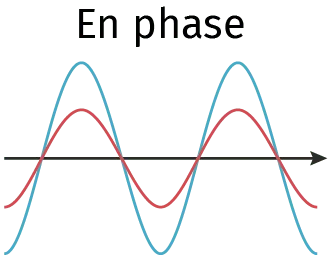
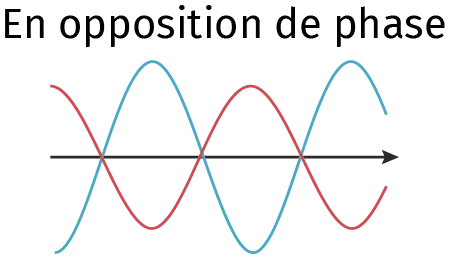
Quelles sont les conditions pour que u et f soient en phase ? En opposition de phase ?
b. Réaliser
Compléter les deux tableaux ci‑dessous en donnant des valeurs de \textrm{A}, \omega et \varphi pour que u et f soient en phase et en opposition de phase.
Afficher, sur le fichier GeoGebra, la fonction u donnée dans l'énoncé.
Quelles sont les conditions pour que u et f soient en phase ? En opposition de phase ?
b. Réaliser
Compléter les deux tableaux ci‑dessous en donnant des valeurs de \textrm{A}, \omega et \varphi pour que u et f soient en phase et en opposition de phase.
Le zoom est accessible dans la version Premium.
| \text{A} | \omega | \varphi | |
|---|---|---|---|
| u(t) | 2 | \frac{2 \pi}{3} \simeq 2,1 | \frac{\pi}{6}\left(30^{\circ}\right) |
| f(t) |
Le zoom est accessible dans la version Premium.
| \text{A} | \omega | \varphi | |
|---|---|---|---|
| u(t) | 2 | \frac{2 \pi}{3} \simeq 2,1 | \frac{\pi}{6}\left(30^{\circ}\right) |
| f(t) |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une tension sinusoïdale s᾽écrit sous la forme {u(t)=\mathrm{U} \sin (\omega t+\varphi)} où
\textrm{U} est la tension maximale, \omega est la pulsation telle que {\omega=\frac{2 \pi}{\mathrm{T}}=2 \pi f} (\text{T} est la période en seconde et f la fréquence du signal en hertz) et \varphi est la phase à l'origine en radian.
Remarque
u(0)=\mathrm{U} \sin (\varphi)
Pour s᾽entraîner :
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah