Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 8
Exercices
Trigonométrie
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fonctions du type \bm{f(t) = a \sin (\omega t + \varphi)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Dans chacun des cas suivants, choisir laquelle des deux courbes représentatives proposées correspond à la fonction donnée. Justifier.
1. f(t)=2 \sin \left(5 t+\frac{\pi}{2}\right)
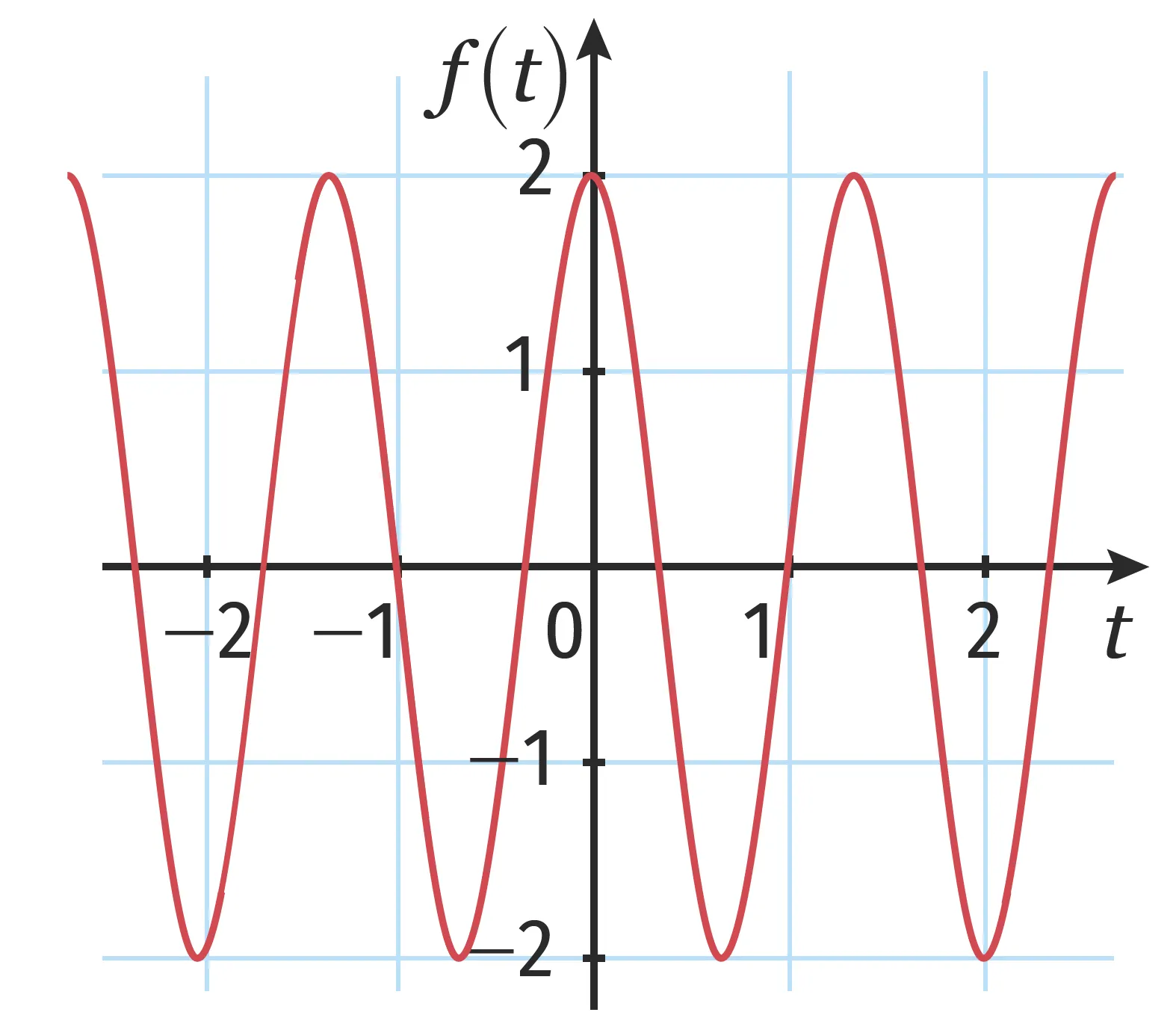
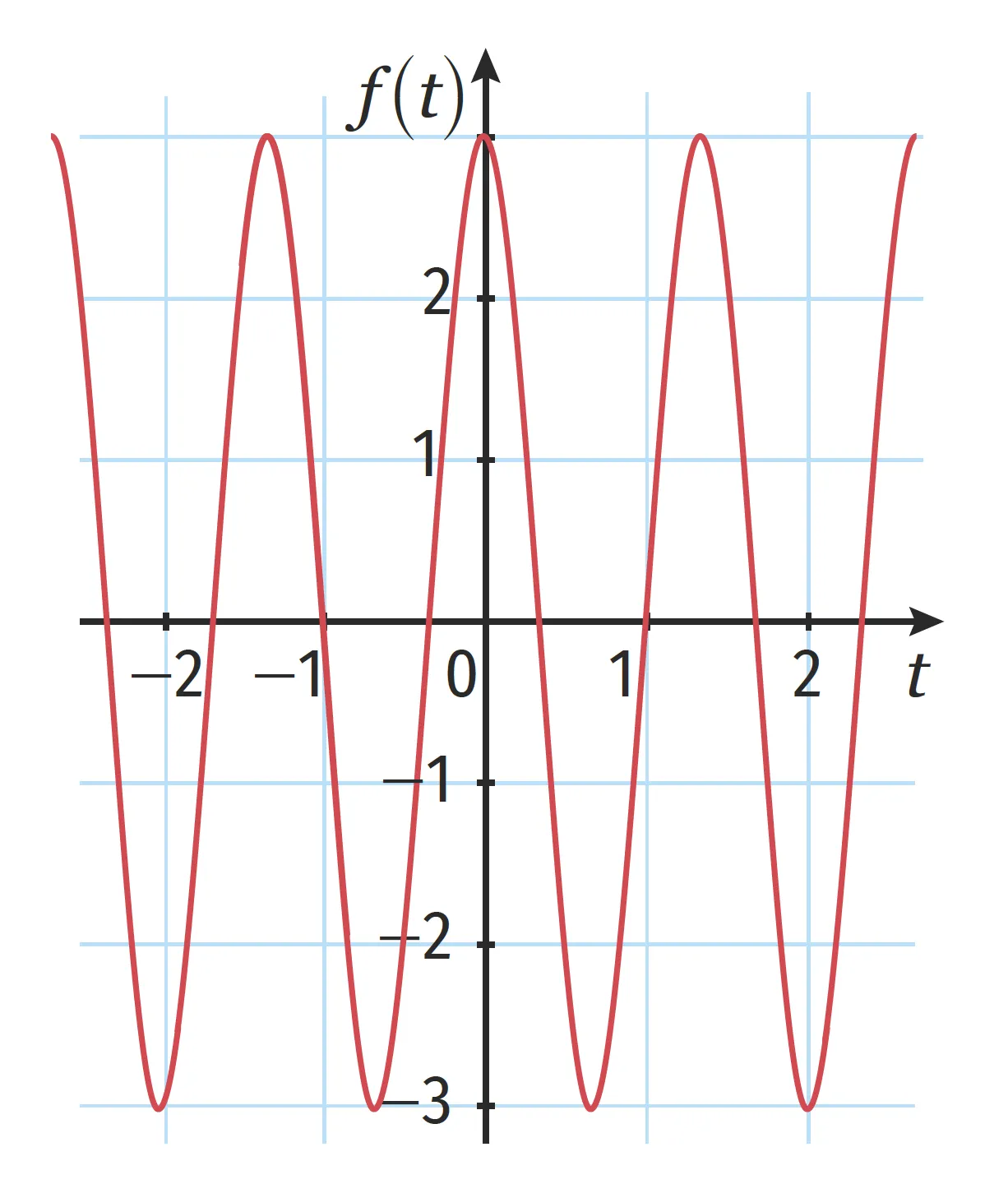
2. g(t)=\frac{1}{2} \sin \left(5 t+\frac{\pi}{3}\right)
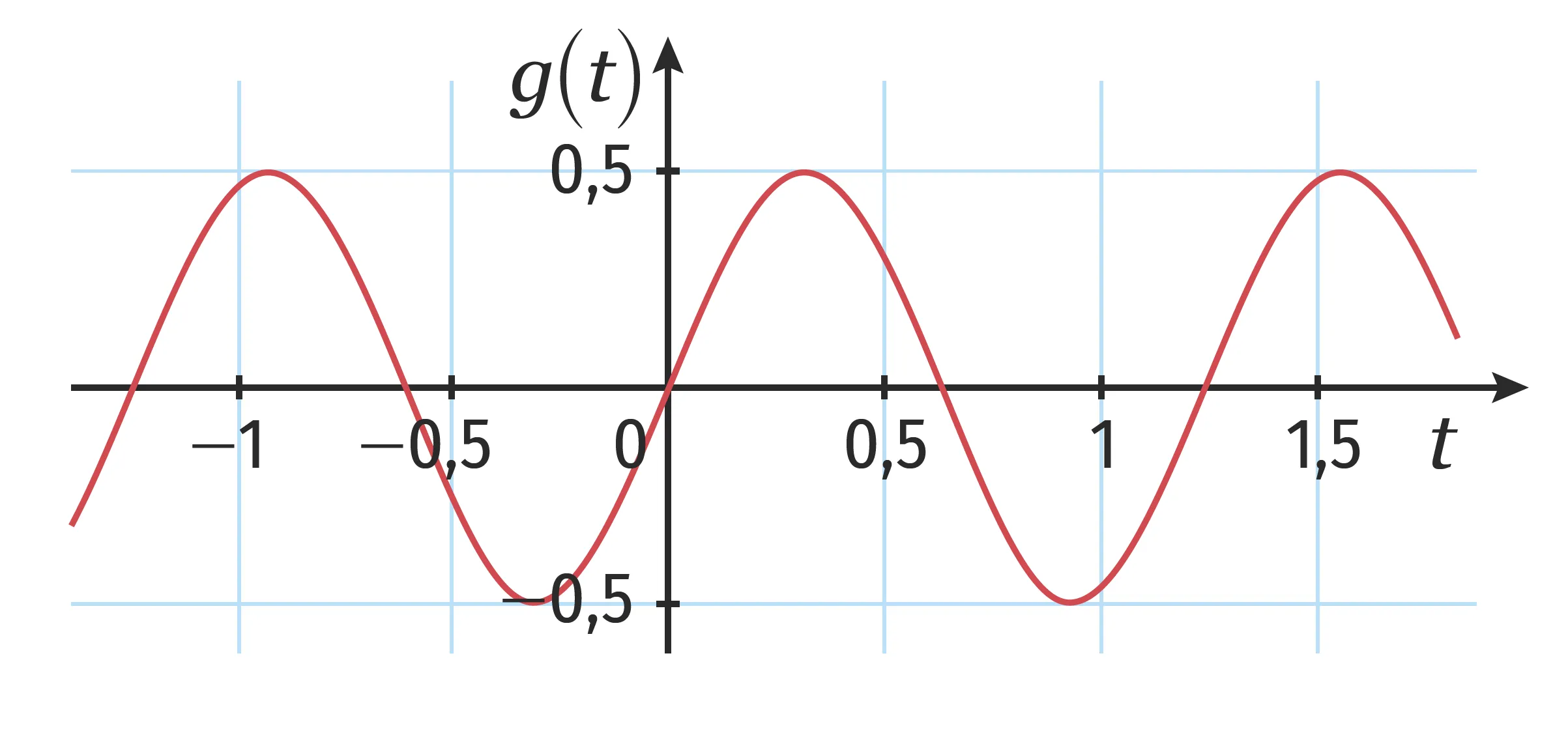
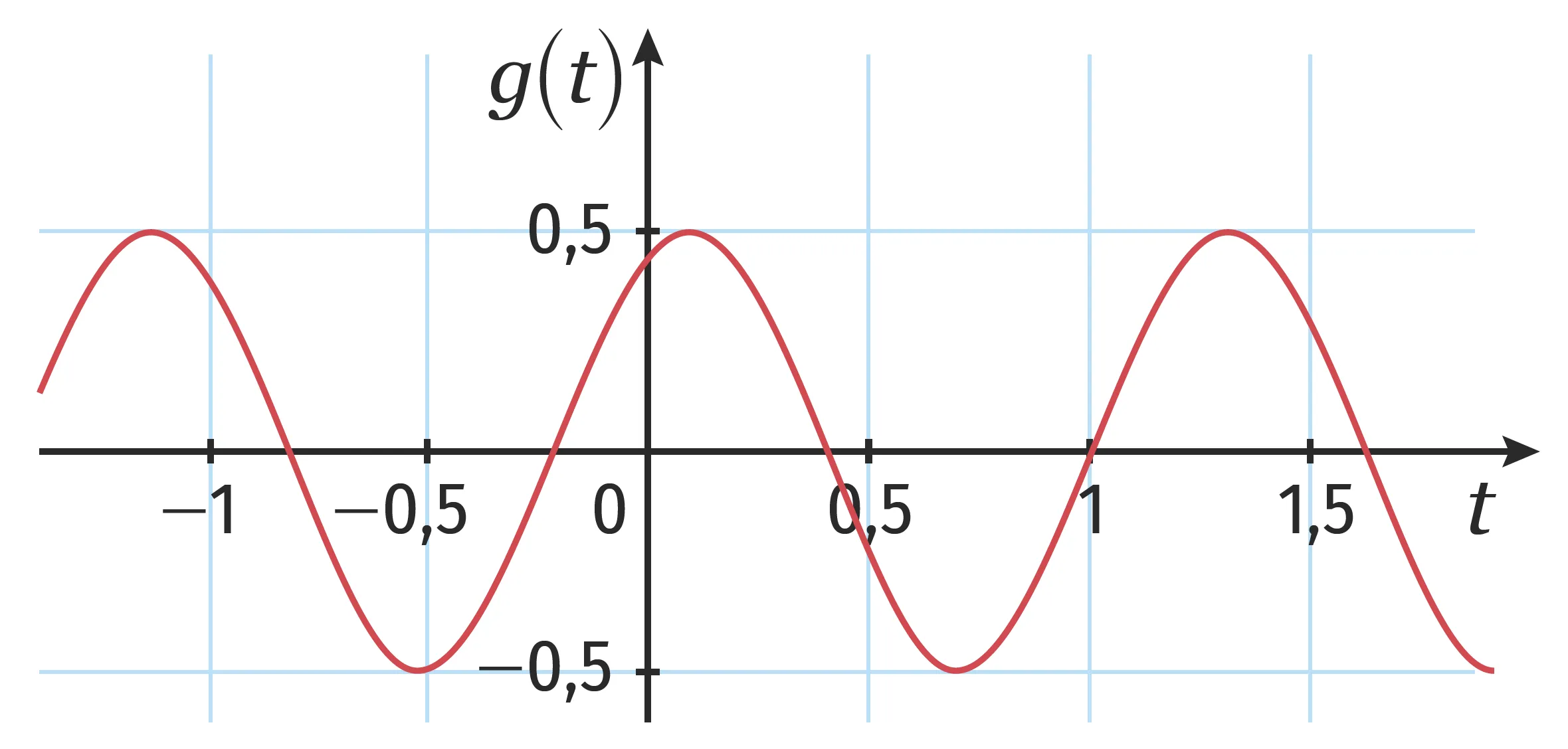
1. f(t)=2 \sin \left(5 t+\frac{\pi}{2}\right)
2. g(t)=\frac{1}{2} \sin \left(5 t+\frac{\pi}{3}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Parmi les fonctions ci‑dessous, lesquelles ont :
1. la même valeur maximale ?
2. la même pulsation ?
3. la même phase à l'origine ?
a. f(t)=\sin (2 t+\pi)
b. g(t)=5 \sin \left(5 t+\frac{\pi}{3}\right)
c. h(t)=5 \sin \left(0,25 t+\frac{\pi}{6}\right)
d. k(t)=6 \sin \left(2 t+\frac{\pi}{6}\right)
e. u(t)=5 \sin \left(2 t+\frac{\pi}{3}\right)
f. v(t)=\sin \left(4 t+\frac{\pi}{2}\right)
1. la même valeur maximale ?
2. la même pulsation ?
3. la même phase à l'origine ?
a. f(t)=\sin (2 t+\pi)
b. g(t)=5 \sin \left(5 t+\frac{\pi}{3}\right)
c. h(t)=5 \sin \left(0,25 t+\frac{\pi}{6}\right)
d. k(t)=6 \sin \left(2 t+\frac{\pi}{6}\right)
e. u(t)=5 \sin \left(2 t+\frac{\pi}{3}\right)
f. v(t)=\sin \left(4 t+\frac{\pi}{2}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
On a représenté ci‑dessous un signal sinusoïdal représentant la fonction f définie par f(t)=\mathrm{A} \sin (\omega t+\varphi) où t représente le temps en seconde.
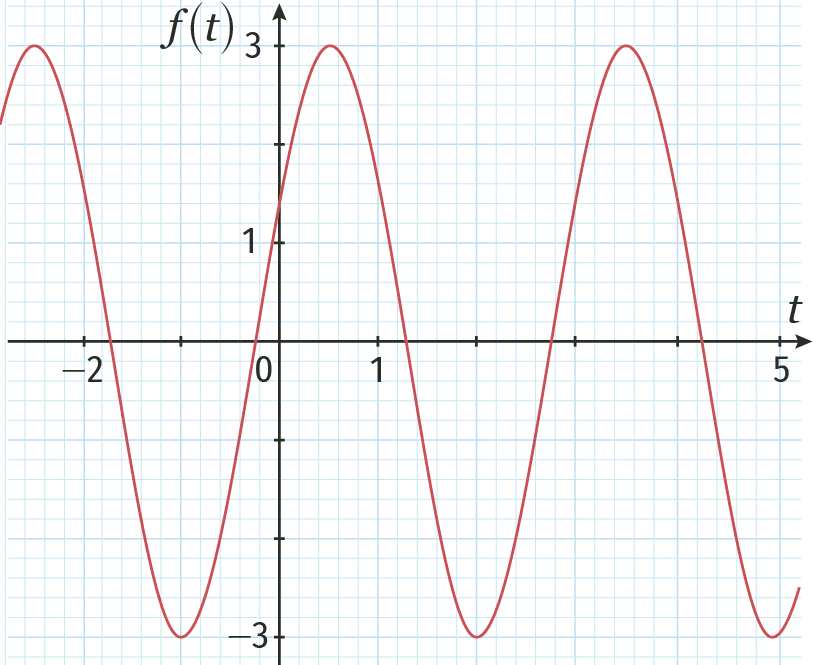
1. Déterminer graphiquement la valeur maximale \text{A} du signal. Déterminer graphiquement la période \text{T} en seconde.
2. En déduire la pulsation \omega=\frac{2 \pi}{\mathrm{T}} en rad/s.
3. Déterminer l'ordonnée exacte du point d'abscisse t = 0 appartenant à la courbe.
4. En déduire une valeur de la phase à l'origine \varphi.
5. Écrire une expression algébrique possible de la fonction f.
1. Déterminer graphiquement la valeur maximale \text{A} du signal. Déterminer graphiquement la période \text{T} en seconde.
GeoGebra
2. En déduire la pulsation \omega=\frac{2 \pi}{\mathrm{T}} en rad/s.
3. Déterminer l'ordonnée exacte du point d'abscisse t = 0 appartenant à la courbe.
4. En déduire une valeur de la phase à l'origine \varphi.
5. Écrire une expression algébrique possible de la fonction f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vecteurs de Fresnel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
Dans un repère, représenter le vecteur de Fresnel de u_{1}(t)=5 \sin \left(2 t+\frac{\pi}{4}\right), de u_{2}(t)=6 \sin \left(2 t+\frac{\pi}{6}\right) puis celui de la grandeur u_3 telle que u_{3}(t)=u_{1}(t)+u_{2}(t).
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5
Les figures 1 à 6 représentent des vecteurs de Fresnel associés à des grandeurs sinusoïdales. Pour chacune d'elles, donner la valeur de la phase à l᾽origine \varphi en radian. L'axe de référence est l'axe horizontal orienté.
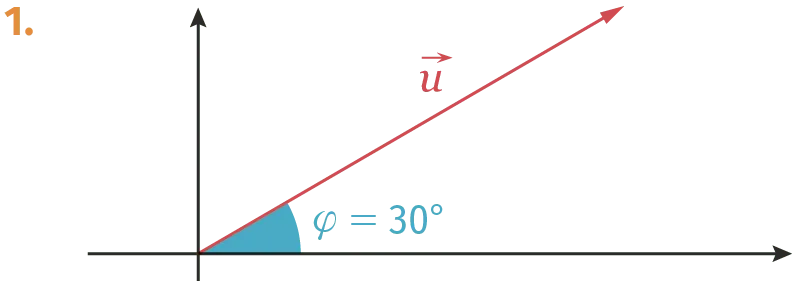
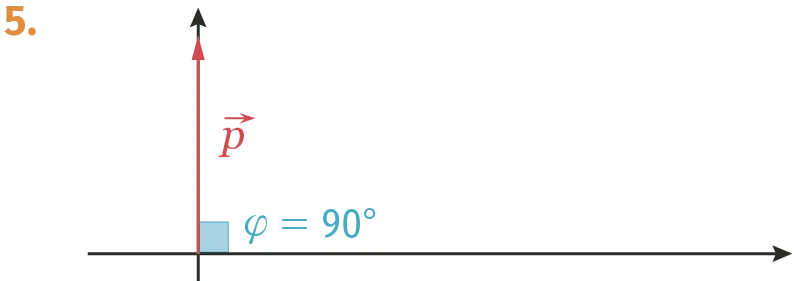
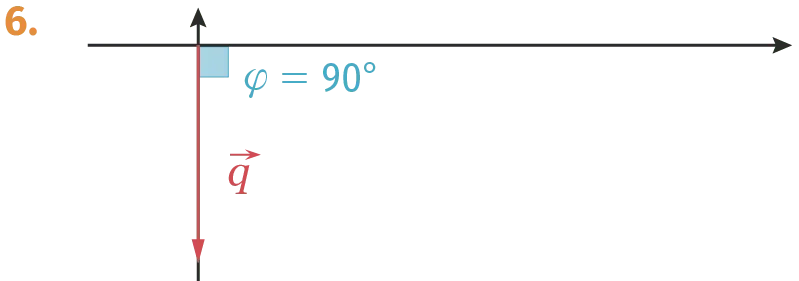
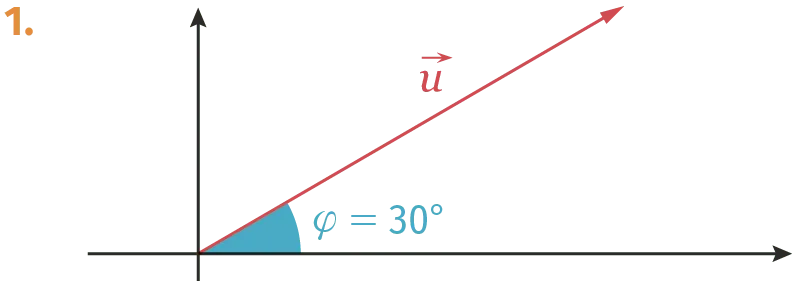
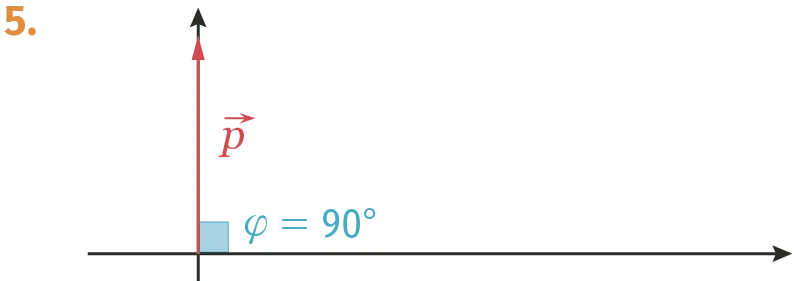
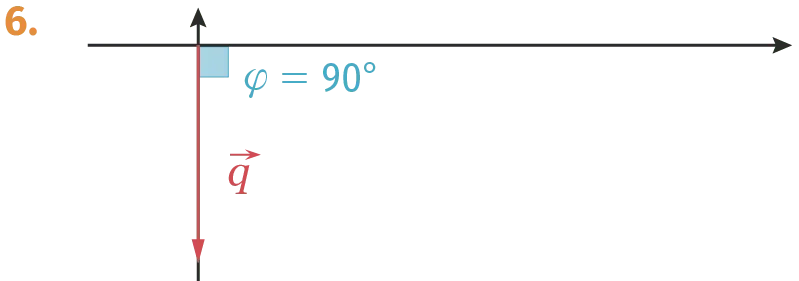
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
Le vecteur de Fresnel d'une grandeur sinusoïdale i de pulsation \omega=341 rad.s-1 est représenté ci-dessous.
Déterminer l'expression algébrique i(t) à laquelle il est associé.
Déterminer l'expression algébrique i(t) à laquelle il est associé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
Dans un repère, représenter le vecteur de Fresnel associé à la fonction sinusoïdale f définie par {f(t)=3 \sin \left(\omega t+\frac{\pi}{3}\right)}.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8
On considère les vecteurs de Fresnel associés à deux grandeurs sinusoïdales u_1 et u_2.
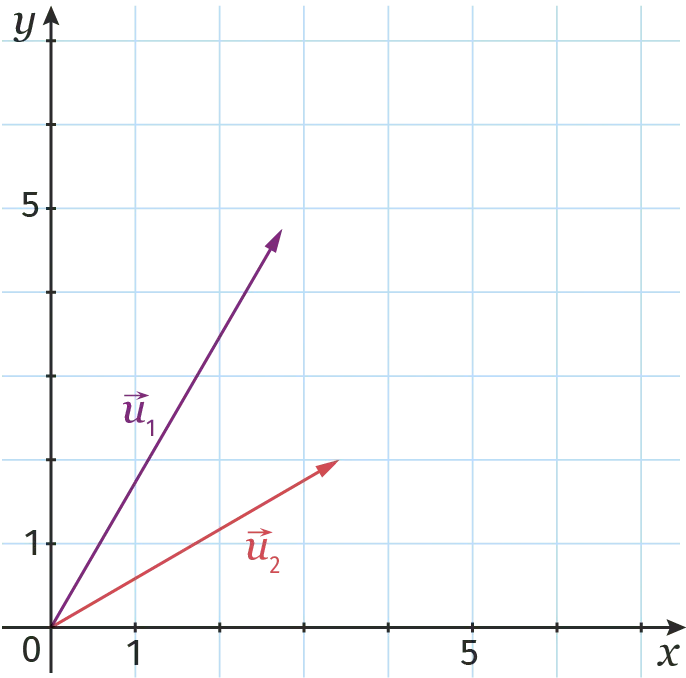
Après avoir reproduit le repère ci‑dessus, tracer le vecteur de Fresnel de la grandeur u_3 telle que {u_{3}(t)=u_{1}(t)+u_{2}(t)}.
Après avoir reproduit le repère ci‑dessus, tracer le vecteur de Fresnel de la grandeur u_3 telle que {u_{3}(t)=u_{1}(t)+u_{2}(t)}.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Équations trigonométriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9
Résoudre sur ]-\pi \: ; \pi] les équations suivantes.
1. \sin (x)=\frac{1}{2}
2. \cos (x)=\frac{\sqrt{2}}{2}
3. \sin (x)=-\frac{\sqrt{3}}{2}
4. 2 \sin \left(x+\frac{\pi}{3}\right)=1
5. 2 \cos \left(x+\frac{\pi}{6}\right)=-\sqrt{3}
1. \sin (x)=\frac{1}{2}
2. \cos (x)=\frac{\sqrt{2}}{2}
3. \sin (x)=-\frac{\sqrt{3}}{2}
4. 2 \sin \left(x+\frac{\pi}{3}\right)=1
5. 2 \cos \left(x+\frac{\pi}{6}\right)=-\sqrt{3}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10
Résoudre les équations suivantes.
1. 2 \cos (2 x)=1 sur \left] - \frac{\pi}{2} \: ; \frac{\pi}{2}\right].
2. 2 \cos (2 x)=-\sqrt{2} sur \left] - \frac{\pi}{2} \: ; \frac{\pi}{2}\right].
3. 2 \sin (3 x)=\sqrt{3} sur \left] - \frac{\pi}{3} \: ; \frac{\pi}{3}\right].
4. 2 \sin (2 x - \frac{\pi}{3})=\sqrt{3} sur \left] - \frac{\pi}{2} \: ; \frac{\pi}{2}\right].
5. 20 \sin (100 \pi x + \frac{\pi}{2})=10 sur \left] -0,01 \: ; 0,01\right].
1. 2 \cos (2 x)=1 sur \left] - \frac{\pi}{2} \: ; \frac{\pi}{2}\right].
2. 2 \cos (2 x)=-\sqrt{2} sur \left] - \frac{\pi}{2} \: ; \frac{\pi}{2}\right].
3. 2 \sin (3 x)=\sqrt{3} sur \left] - \frac{\pi}{3} \: ; \frac{\pi}{3}\right].
4. 2 \sin (2 x - \frac{\pi}{3})=\sqrt{3} sur \left] - \frac{\pi}{2} \: ; \frac{\pi}{2}\right].
5. 20 \sin (100 \pi x + \frac{\pi}{2})=10 sur \left] -0,01 \: ; 0,01\right].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 11
Outil numérique
Représenter les deux fonctions u et i définies par {u(t)=6 \sin \left(\frac{\pi}{2} t-\frac{\pi}{3}\right)} et {i(t)=2 \sin \left(\frac{\pi}{2} t-\frac{\pi}{4}\right)} ainsi que leurs vecteurs de Fresnel associés.
Que peut-on conclure sur leur déphasage ?
GeoGebra
Que peut-on conclure sur leur déphasage ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12
Outil numérique
On considère les trois intensités suivantes.
1. Représenter le vecteur de Fresnel de chacune de ces intensités.
2. En déduire l'écriture algébrique de i(t)=i_{1}(t)+i_{2}(t)+i_{3}(t).
2. Vérifier ce résultat en traçant ci-dessus i(t) et i_{1}(t)+i_{2}(t)+i_{3}(t).
- i_{1}(t)=2 \sin (\pi t)
- i_{2}(t)=2,5 \sin \left(\pi t+\frac{\pi}{4}\right)
- i_{3}(t)=3 \sin \left(\pi t-\frac{\pi}{3}\right)
1. Représenter le vecteur de Fresnel de chacune de ces intensités.
GeoGebra
2. En déduire l'écriture algébrique de i(t)=i_{1}(t)+i_{2}(t)+i_{3}(t).
2. Vérifier ce résultat en traçant ci-dessus i(t) et i_{1}(t)+i_{2}(t)+i_{3}(t).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
Une distribution triphasée est composée de trois tensions simples de même fréquence, de même amplitude et déphasées.
- u_{1}(t)=230 \sin (100 \pi t)
- u_{2}(t)=230 \sin \left(100 \pi t+\frac{2 \pi}{3}\right)
- u_{3}(t)=230 \sin \left(100 \pi t-\frac{2 \pi}{3}\right)
1. Associer à chaque courbe la tension correspondante.
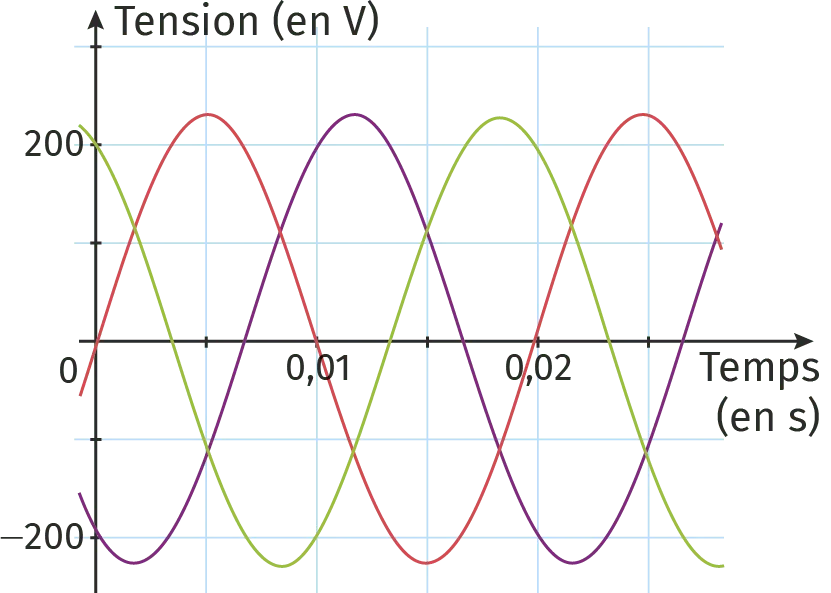
2. Tracer les vecteurs de Fresnel de ces trois tensions dans un même repère.
GeoGebra
3. Quelle est la somme de ces trois tensions ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
On a représenté ci‑dessous le schéma électrique d'une maille.
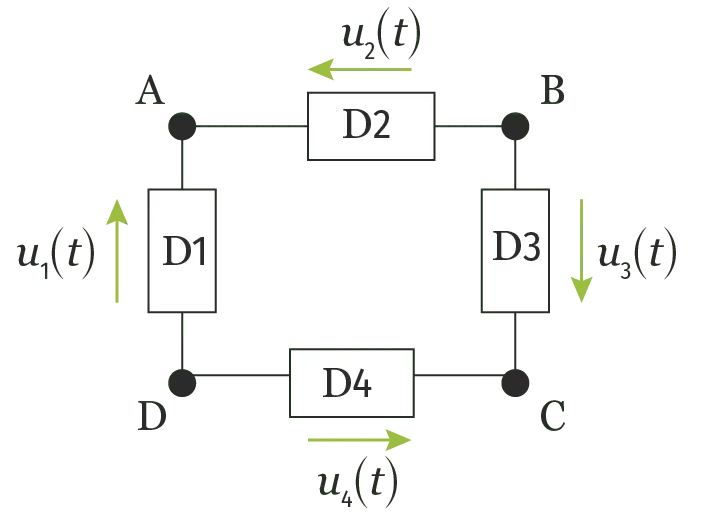
On considère que {u_{1}(t)=6 \sin \left(314 t+\frac{\pi}{3}\right)}, {u_{2}(t)=8 \sin \left(314 t-\frac{\pi}{6}\right)} et {u_{3}(t)=10 \sin \left(314 t+\frac{3 \pi}{4}\right)}.
Déterminer la tension u_4(t) par la méthode des vecteurs de Fresnel.
On considère que {u_{1}(t)=6 \sin \left(314 t+\frac{\pi}{3}\right)}, {u_{2}(t)=8 \sin \left(314 t-\frac{\pi}{6}\right)} et {u_{3}(t)=10 \sin \left(314 t+\frac{3 \pi}{4}\right)}.
Déterminer la tension u_4(t) par la méthode des vecteurs de Fresnel.
Aide
D᾽après la loi des mailles, on a ici {u_{4}(t)=u_{1}(t)-u_{2}(t)+u_{3}(t)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15
Résoudre les équations suivantes en donnant, lorsque c'est possible, les solutions exactes et les solutions numériques approchées à 0,1 près en radian.
1. \sin (x)=\frac{\sqrt{3}}{2} sur ]-\pi \: ; \pi].
2. \cos (x)=\frac{1}{2} sur ]-\pi \: ; \pi].
3. 2\sin (x)=-1 sur ]-\pi \: ; \pi].
4. 2\cos (x)=\sqrt{3} sur ]-\pi \: ; \pi].
5. \sin (\pi x + \frac{2 \pi}{3})=1 sur [-1 \: ; 1].
6. 2 \sin \left(x-\frac{\pi}{3}\right)=\sqrt{3} sur ]-\pi \: ; \pi].
1. \sin (x)=\frac{\sqrt{3}}{2} sur ]-\pi \: ; \pi].
2. \cos (x)=\frac{1}{2} sur ]-\pi \: ; \pi].
3. 2\sin (x)=-1 sur ]-\pi \: ; \pi].
4. 2\cos (x)=\sqrt{3} sur ]-\pi \: ; \pi].
5. \sin (\pi x + \frac{2 \pi}{3})=1 sur [-1 \: ; 1].
6. 2 \sin \left(x-\frac{\pi}{3}\right)=\sqrt{3} sur ]-\pi \: ; \pi].
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah