Chapitre 8
Activité B
Vecteurs de Fresnel
Capacité : Utiliser les vecteurs de Fresnel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On considère un nœud électrique où arrivent deux intensités sinusoïdales i_1 et i_2.
- {i_{1}(t)=2 \sin \left(\frac{2 \pi}{3} t+\frac{\pi}{6}\right)}
- {i_{2}(t)=3 \sin \left(\frac{2 \pi}{3} t+\frac{\pi}{3}\right)}

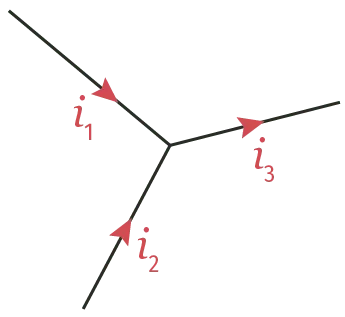
Problématique
Problématique : Quelle est l'expression algébrique de \boldsymbol{i}_\bm{3}(\boldsymbol{t}) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Analyser/Raisonner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Réaliser
Aide
Selon la loi des nœuds, la somme des intensités arrivant à un nœud est égale à la somme des intensités qui en repartent.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3S'approprier
La somme de deux signaux sinusoïdaux de même pulsation \bm{\omega} est un signal
sinusoïdal de pulsation identique \bm{\omega}. On peut donc écrire i_3 sous la forme {i_{3}(t)=\mathrm{A} \sin \left(\frac{2 \pi}{3} t+\varphi\right)} avec \text{A} et \varphi deux grandeurs à déterminer.
En s'aidant de l'exemple sur i_1, compléter la ligne i_2 du tableau ci‑dessous.
En s'aidant de l'exemple sur i_1, compléter la ligne i_2 du tableau ci‑dessous.
| Grandeur sinusoïdale | Vecteur de Fresnel | Représentation graphique |
|---|---|---|
| i_{1}(t)=\color{#7D3681}2 \color{black} \sin \left(\frac{2 \pi}{3} t+ \color{#A2C946} \frac{\pi}{6} \color{black} \right) | \overrightarrow{i_{1}}\left(\color{#7D3681} 2 \: \color{black} ; \color{#A2C946} \frac{\pi}{6} \color{black} \right) |
 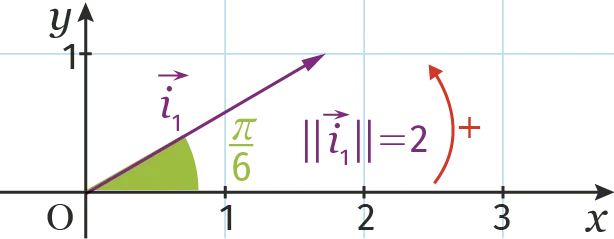 |
| i_{2}(t)=3 \sin \left(\frac{2 \pi}{3} t+\frac{\pi}{3}\right) |
Cliquez pour accéder à une zone de dessin | |
| i_{3}(t)=\ldots \sin \left(\frac{2 \pi}{3} t+\ldots\right) |
Cliquez pour accéder à une zone de dessin |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Réaliser
Tracer sur un graphique le vecteur \vec{i}_{3}=\vec{i}_{1}+\vec{i}_{2} à partir de l'origine \text{O}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Analyser/Raisonner, réaliser
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Analyser/Raisonner, communiquer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour toute fonction sinusoïdale i définie par i(t)=\mathrm{I} \sin (\omega t+\varphi), on peut associer un vecteur de Fresnel \overrightarrow{i} dont les caractéristiques sont les suivantes :
Pour obtenir l'expression algébrique de la somme de plusieurs grandeurs sinusoïdales de même fréquence, on peut additionner les vecteurs de Fresnel associés à chaque grandeur puis utiliser les coordonnées du vecteur ainsi obtenu.

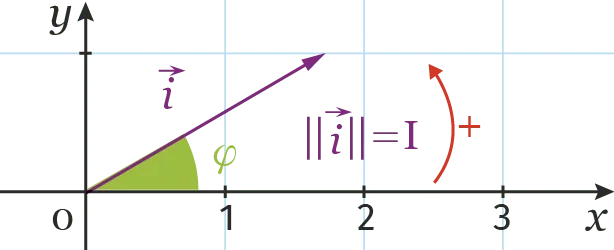
- son origine est en \text{O} ;
- l'angle entre l'axe des abcisses et le vecteur \overrightarrow{i} est égal à \varphi ;
- sa norme est égale à la valeur maximale de i(t), soit \text{I}.
Pour obtenir l'expression algébrique de la somme de plusieurs grandeurs sinusoïdales de même fréquence, on peut additionner les vecteurs de Fresnel associés à chaque grandeur puis utiliser les coordonnées du vecteur ainsi obtenu.

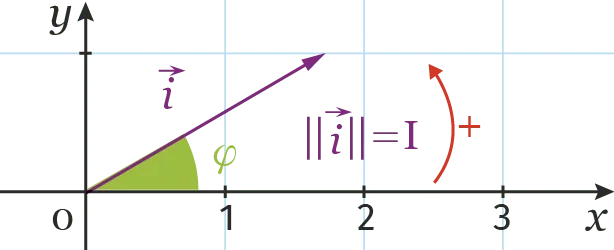
Pour s᾽entraîner : et
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

