Chapitre 5
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compétence : Travailler en autonomie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Notion de référentiel
- En mécanique, un système dont on étudie le mouvement est appelé un mobile.
- L'objet par rapport auquel on repère la position d'un mobile est appelé un référentiel.
- Dans une description exacte du mouvement d'un mobile, le référentiel d'étude est précisé.
- La trajectoire d'un mobile dépend du référentiel choisi.
Le saviez-vous ?
Le mouvement d'un système dépend du référentiel dans lequel on l'observe.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Nature du mouvement et référentiel
Si dans le référentiel choisi :
- la trajectoire d'un mobile est une droite, alors son mouvement est rectiligne dans ce référentiel ;
- la trajectoire d'un mobile est un cercle, alors son mouvement est circulaire dans ce référentiel ;
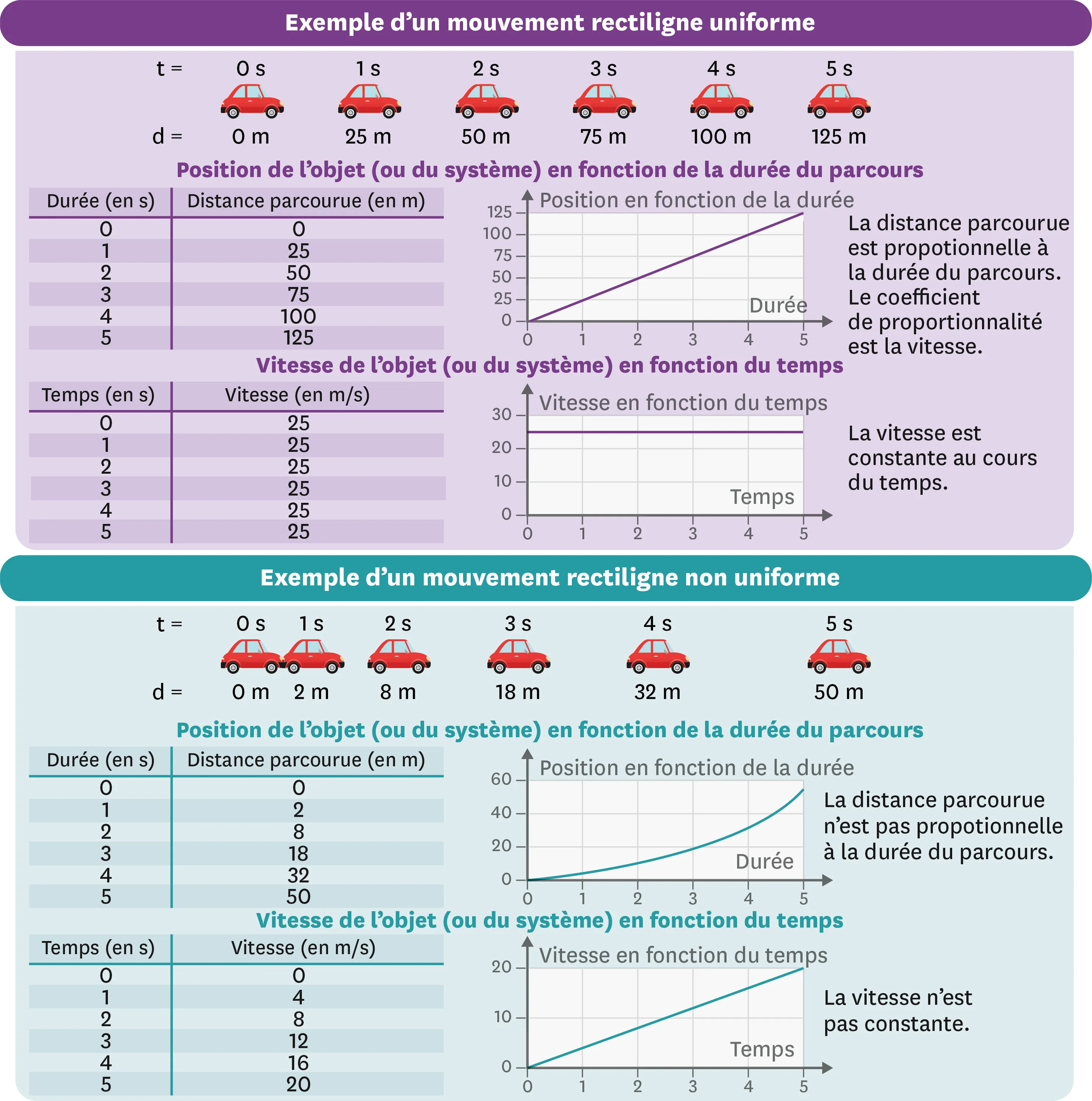
- la valeur de la vitesse d'un mobile est constante, alors le mouvement est un mouvement uniforme dans ce référentiel.
Le saviez-vous ?
Si la valeur de la vitesse d'un mobile est constante, alors son mouvement est uniforme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Nature du mouvement et chronophotographie
- Lors d'un mouvement uniforme, la chronophotographie du mobile présente des positions successives toujours espacées de la même distance.
- Lors d'un mouvement non uniforme, la chronophotographie du mobile présente des positions successives espacées de distances différentes.
- Lors d'un mouvement uniforme, la distance parcourue par un mobile en une durée donnée est proportionnelle à la valeur de la vitesse.
Le saviez-vous ?
Sur une chronophotographie, si les positions sont espacées régulièrement, alors le mouvement est uniforme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Relation durée, distance, vitesse moyenne
- La vitesse moyenne d'un objet dépend du référentiel.
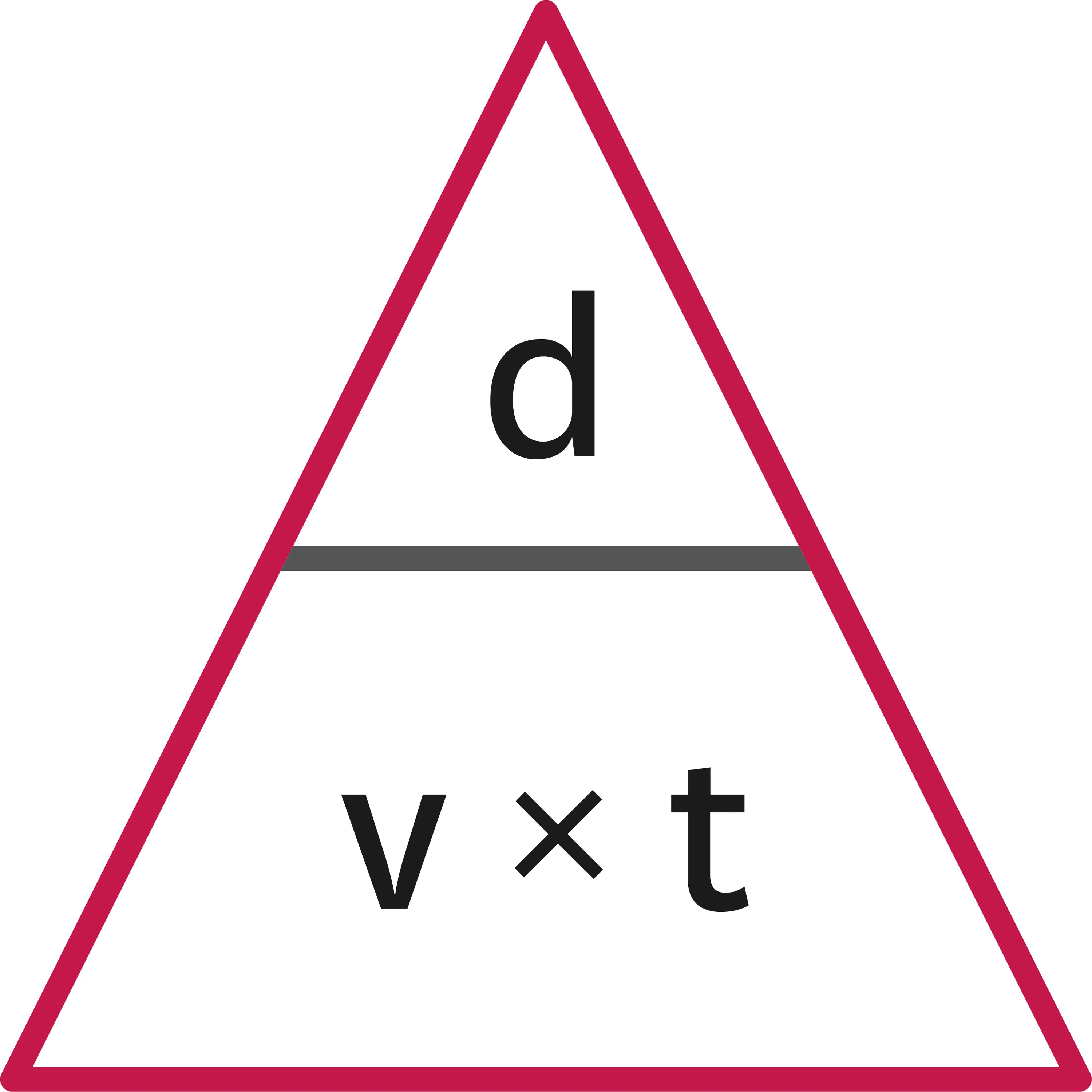
- Dans un référentiel donné, la vitesse moyenne v d'un mobile est liée à la distance totale d parcourue lors du mouvement et à la durée total t de ce mouvement.
- La relation accepte trois formulations équivalentes : v = \dfrac{d}{t} t = \dfrac{d}{v} d = v \times t
- L'écriture ci-contre permet de rassembler ces trois égalités. En cachant le symbole de la grandeur cherchée, on voit apparaitre l'opération devant être faite avec les deux autres grandeurs.
Le saviez-vous ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Référentiel : activité 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je retiens par l'image

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


