Chapitre 5
Cours
Évolution temporelle d'une transformation nucléaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Désintégration radioactive
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AStabilité et instabilité des noyaux
On connaît à ce jour 118 éléments chimiques. Les éléments présentent un grand nombre d'isotopes : si certains (environ 300) sont stables ou quasi stables, la grande majorité d'entre eux sont instables et considérés comme radioactifs (environ 3 000).
Un noyau est dit radioactif s'il peut se désintégrer spontanément en libérant une particule et de l'énergie. Cette désintégration s'effectue aléatoirement dans le temps. Lors d'une désintégration, il y a entre le noyau père et le(s) noyau(x) fils :
Ces lois de conservations sont appelées lois de Soddy.
- conservation du nombre de charges électriques Z ;
- conservation du nombre de masse A.
Ces lois de conservations sont appelées lois de Soddy.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1 Découverte de la radioactivité

Henri Becquerel découvre la radioactivité en 1896 en réalisant une impression photographique avec du minerai d'uranium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BDifférentes radioactivités
Lors de sa désintégration, le noyau peut émettre différentes particules qui dépendent de son instabilité.
Exemples :
Le noyau d'uranium 238 libère un noyau d'hélium : (α)
_{\thickspace 92}^{238}\text{U} \rightarrow \ ^{234}_{\thickspace 90}\text{Th} + \ ^4_2\text{He}
Le noyau de carbone 14 libère un électron : (β-)
^{14}_{\; 6}\text{C} \rightarrow \ ^{14}_{\; 7}\text{N} +\ _{-1}^{\enspace 0}\text{e}^-
Le noyau de soufre 30 libère un positon : (β+)
_{16}^{30}\text{S} \rightarrow \ ^{30}_{15}\text{P} + \ ^0_1\text{e}^+
Radioactivité α :
Elle concerne les noyaux instables très lourds (excès de nucléons). Lors de cette désintégration, il y a émission d'un noyau d'hélium, appelé particule α :
Radioactivité β- :
Les noyaux instables possédant un excès de neutrons se désintègrent en libérant un électron :
Radioactivité β+ :
Les noyaux instables possédant un excès de protons se désintègrent en libérant un positon :
Radioactivité γ :
Après la désintégration d'un noyau radioactif α ou β, le noyau obtenu se trouve généralement dans un état excité. Pour gagner en stabilité, ce noyau émet un photon de très grande énergie :
Elle concerne les noyaux instables très lourds (excès de nucléons). Lors de cette désintégration, il y a émission d'un noyau d'hélium, appelé particule α :
^A_Z\text{X} \rightarrow \ ^{A-4}_{Z-2}\text{Y} + \ ^4_2\text{He}
Radioactivité β- :
Les noyaux instables possédant un excès de neutrons se désintègrent en libérant un électron :
^A_Z\text{X} \rightarrow \ ^{\quad A}_{Z+1}\text{Y} + \ ^{\enspace 0}_{-1}\text{e}^-
Radioactivité β+ :
Les noyaux instables possédant un excès de protons se désintègrent en libérant un positon :
^A_Z\text{X} \rightarrow \ ^{\quad A}_{Z-1}\text{Y} + \ ^0_1\text{e}^+
Radioactivité γ :
Après la désintégration d'un noyau radioactif α ou β, le noyau obtenu se trouve généralement dans un état excité. Pour gagner en stabilité, ce noyau émet un photon de très grande énergie :
^A_Z\text{Y}^* \rightarrow \ ^A_Z\text{Y} + \,γ
Exemples :
Le noyau d'uranium 238 libère un noyau d'hélium : (α)
_{\thickspace 92}^{238}\text{U} \rightarrow \ ^{234}_{\thickspace 90}\text{Th} + \ ^4_2\text{He}
Le noyau de carbone 14 libère un électron : (β-)
^{14}_{\; 6}\text{C} \rightarrow \ ^{14}_{\; 7}\text{N} +\ _{-1}^{\enspace 0}\text{e}^-
Le noyau de soufre 30 libère un positon : (β+)
_{16}^{30}\text{S} \rightarrow \ ^{30}_{15}\text{P} + \ ^0_1\text{e}^+
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
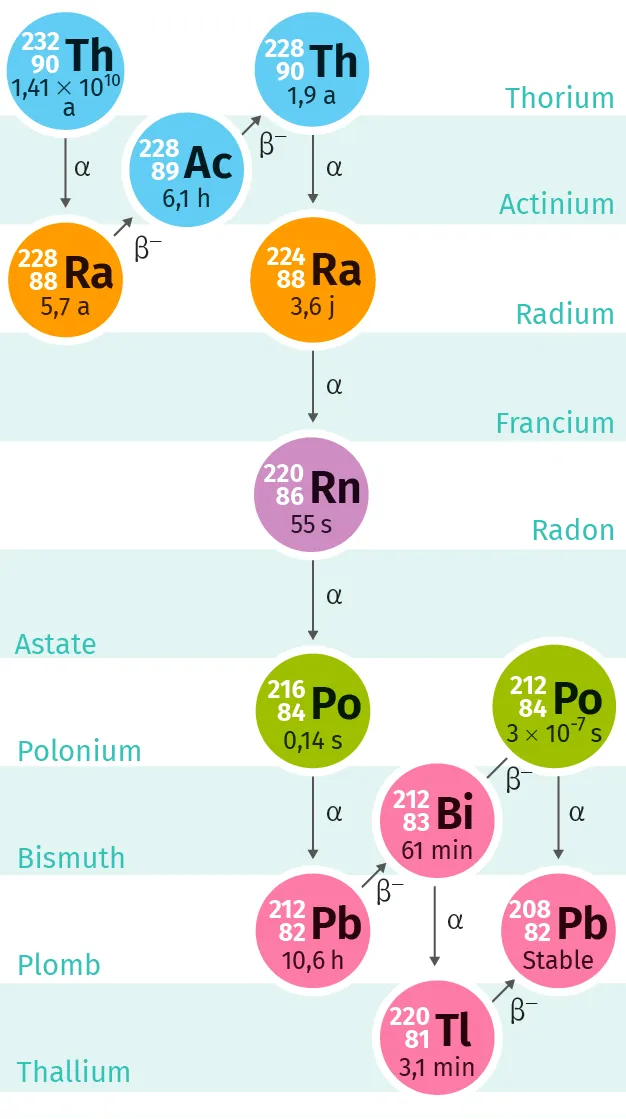
Doc. 2 Chaîne de désintégrations

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les électrons et les positons émis par les deux types de radioactivité β sont créés lors de la désintégration d'un neutron en proton (radioactivité β-) ou d'un proton en neutron (radioactivité β+).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
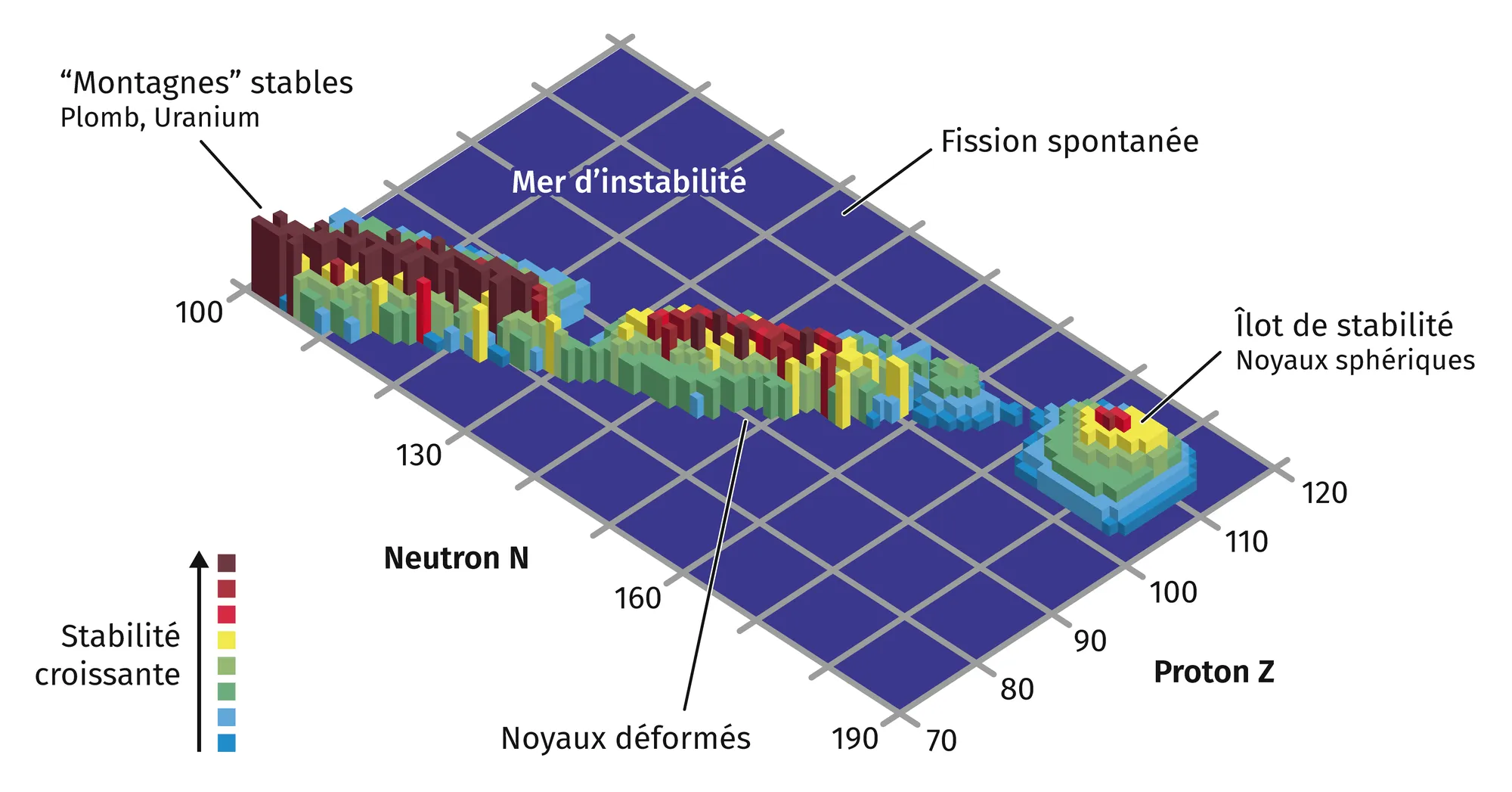
Diagramme représentant la stabilité des isotopes

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3 Sources d'exposition à la radioactivité

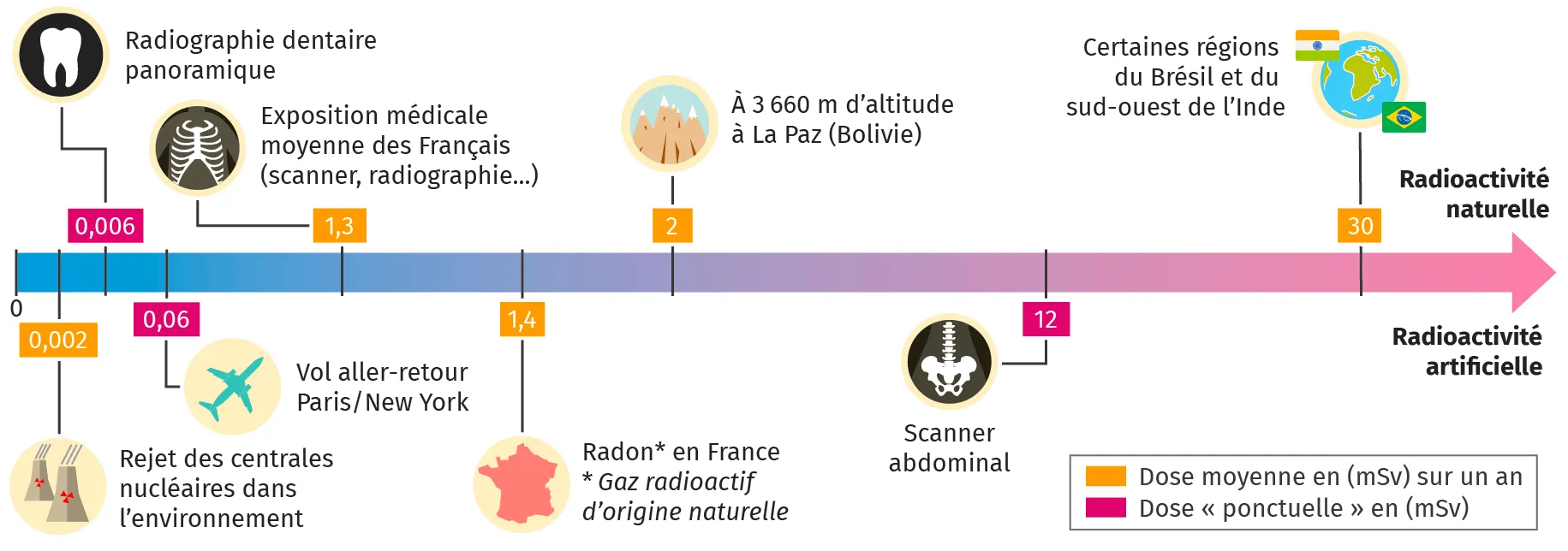
Le sievert (Sv) est une unité utilisée pour évaluer l'impact de rayonnements radioactifs sur le corps humain, basée sur l'énergie absorbée par kilogramme de masse corporelle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CDangers et effets biologiques
La radioactivité est mise à profit dans de nombreuses applications, notamment dans l'imagerie médicale ou encore en radiothérapie pour détruire des cellules cancéreuses.
Elle est également répandue dans l'industrie afin de stériliser des aliments ou des objets, mais son utilisation n'est pas sans risque.
La radioactivité absorbée par le corps peut être soit ponctuelle comme lors d'un examen médical, soit permanente avec la radioactivité naturelle de l'environnement.
Les méthodes de protection dépendent du type de radioactivités et de la durée d'exposition. Les particules \alpha ont un rayonnement hautement ionisant, contrairement aux particules \beta ou \gamma, mais elles ont une pénétration dans le corps humain plus faible que ces dernières. Ces expositions peuvent entraîner des problèmes de santé, dont de nombreux cancers.
Elle est également répandue dans l'industrie afin de stériliser des aliments ou des objets, mais son utilisation n'est pas sans risque.
La radioactivité absorbée par le corps peut être soit ponctuelle comme lors d'un examen médical, soit permanente avec la radioactivité naturelle de l'environnement.
Les méthodes de protection dépendent du type de radioactivités et de la durée d'exposition. Les particules \alpha ont un rayonnement hautement ionisant, contrairement aux particules \beta ou \gamma, mais elles ont une pénétration dans le corps humain plus faible que ces dernières. Ces expositions peuvent entraîner des problèmes de santé, dont de nombreux cancers.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Tomographie d'un cerveau

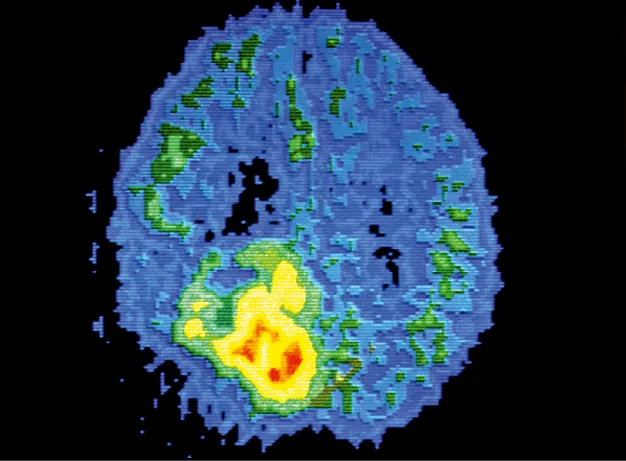
Cette technique médicale met à profit la radioactivité \beta ^+ pour identifier la présence de tumeurs cancéreuses.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Squelettes humains vus aux rayons X

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Décroissance radioactive
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AActivité d'un échantillon
La désintégration d'un noyau radioactif est un phénomène aléatoire. Bien que la désintégration d'un noyau ne soit pas prévisible, on peut prévoir l'évolution de la quantité de noyaux radioactifs dans un grand
échantillon.
Le temps de demi-vie est la durée au bout de laquelle l'activité et le nombre de noyaux radioactifs ont diminué de moitié.
A = \lambda \cdot N
A : activité radioactive (Bq)
\lambda : constante radioactive (s-1)
N : nombre de noyaux radioactifs
\lambda : constante radioactive (s-1)
N : nombre de noyaux radioactifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6Exemples d'activité
| Source | Activité (Bq) |
|---|---|
| Eau douce (1 L) | 1 |
| Légumes (1 kg) | 150 |
| Engrais (1 kg) | 5 000 |
| Corps humain (70 kg) | 8 000 |
| Uranium 238 (1 g) | 12 000 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLoi de décroissance radioactive
On peut déterminer numériquement à un instant t la quantité N(t) de noyaux radioactifs non désintégrés d'une population initiale N_0. Pour cela, on utilise la loi de décroissance radioactive. L'activité correspond
au nombre de désintégrations par unité de temps : elle est également proportionnelle au nombre de noyaux restants N(t) :
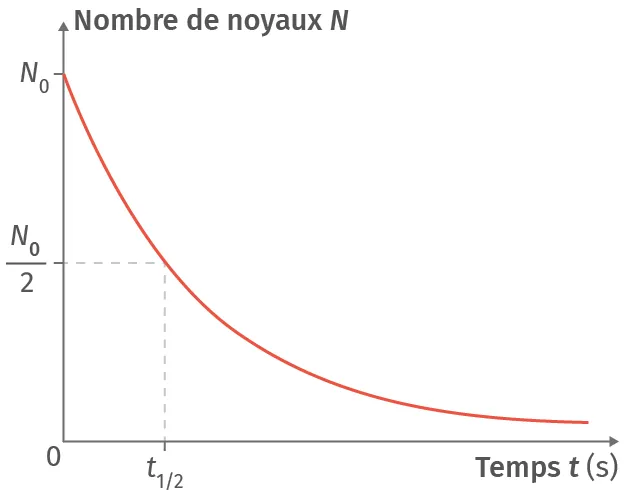
Le nombre de noyaux radioactifs N(t) au cours du temps suit une loi de décroissance radioactive.
\begin{cases}
A = &- \dfrac{\text{d}N}{\text{d}t} \\
A = &\lambda \cdot N
\end{cases}
\dfrac{\text{d}N}{\text{d}t} + \lambda \cdot N = 0
N(t) = N_0 \cdot \text{exp}(- \lambda \cdot t)
Soit l'équation différentielle :
\dfrac{\text{d}N}{\text{d}t} + \lambda \cdot N = 0
N(t) = N_0 \cdot \text{exp}(- \lambda \cdot t)
Le nombre de noyaux radioactifs N(t) au cours du temps suit une loi de décroissance radioactive.
Le temps de demi-vie t_{1/2} et la constante radioactive sont liés par la relation :
\lambda = \dfrac{\text{ln}(2)}{t_{1/2}}
\lambda = \dfrac{\text{ln}(2)}{t_{1/2}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Équation différentielle temporelle
Équation différentielle temporelle : équation mettant en relation une grandeur dépendant du temps avec une ou plusieurs de ses dérivées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Courbe de décroissance

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 8Quelques temps de demi-vie
| Isotopes radioactifs | Temps de demi-vie (a) |
|---|---|
| _4^8\text{Be} | 2{,}12 \times 10^{-24} |
| _{\;53}^{131}\text{I} | 2{,}20 \times 10^{-2} |
| _{27}^{60}\text{Co} | 5{,}27 |
| _{\;6}^{14}\text{C} | 5{,}73 \times 10^3 |
| _{\thickspace 53}^{129}\text{I} | 1{,}57 \times 10^7 |
| _{\thickspace 90}^{232}\text{Th} | 1{,}41 \times 10^9 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Datation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
La radioactivité est un phénomène naturel omniprésent. Cette activité est aussi présente dans les roches et dans les organismes. Lorsque ceux-ci ne renouvellent plus la quantité d'isotopes par des échanges
avec l'extérieur, l'activité radioactive décroît. Si la population initiale N_0 en noyaux radioactifs est connue, une mesure de N à un instant t peut permettre une datation.
Pour choisir un isotope radioactif lors d'une datation, il faut que :
- l'isotope soit présent initialement dans l'organisme ou l'objet à dater ;
- le temps de demi-vie t_{1/2} de l'isotope ne soit pas trop court par rapport à l'âge de l'échantillon analysé.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ApplicationDatation au potassium 40 d'une roche
Lors de sa formation, une roche contient initialement 7,22 × 1018 noyaux de potassium 40 et n'en possède plus que 7,60 × 1017. Dater la formation de cette roche à l'aide du .
Corrigé
t = \dfrac{t_{1/2}}{\text{ln}(2)} \cdot \text{ln} \bigg( \dfrac{N_0}{N(t)} \bigg)
AN : t = \dfrac{1{,}25 \times 10^9}{\text{ln}(2)} \times \text{ln} \bigg( \dfrac{7{,}22 \times 10^{18}}{7{,}60 \times 10^{17}} \bigg) = 4{,}06 \times 10^9 \ \text{a}
AN : t = \dfrac{1{,}25 \times 10^9}{\text{ln}(2)} \times \text{ln} \bigg( \dfrac{7{,}22 \times 10^{18}}{7{,}60 \times 10^{17}} \bigg) = 4{,}06 \times 10^9 \ \text{a}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On note τ la constante de temps radioactive :
τ = \dfrac{1}{\lambda} = \dfrac{t_{1/2}}{\text{ln}(2)} - Au bout de 5 τ, 99 % des noyaux se sont désintégrés. La datation n'est plus fiable à partir de cette date.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23} mol‑1
- Demi-vie du potassium 40 : t_{1/2} = 1{,}25 \times 10^9 a
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 9Démonstration
N(t) = N_0 \cdot \text{exp}(-\lambda \cdot t)
\text{ln}(N(t)) = \text{ln}(N_0) - \lambda \cdot t
\lambda \cdot t = \text{ln}(N_0) - \text{ln}(N(t))
t = \dfrac{1}{\lambda} \cdot \ln \bigg(\dfrac{N_0}{N(t)} \bigg) = \dfrac{t_{1/2}}{\ln(2)} \cdot \ln \bigg( \dfrac{N_0}{N(t)} \bigg)
\text{ln}(N(t)) = \text{ln}(N_0) - \lambda \cdot t
\lambda \cdot t = \text{ln}(N_0) - \text{ln}(N(t))
t = \dfrac{1}{\lambda} \cdot \ln \bigg(\dfrac{N_0}{N(t)} \bigg) = \dfrac{t_{1/2}}{\ln(2)} \cdot \ln \bigg( \dfrac{N_0}{N(t)} \bigg)
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

