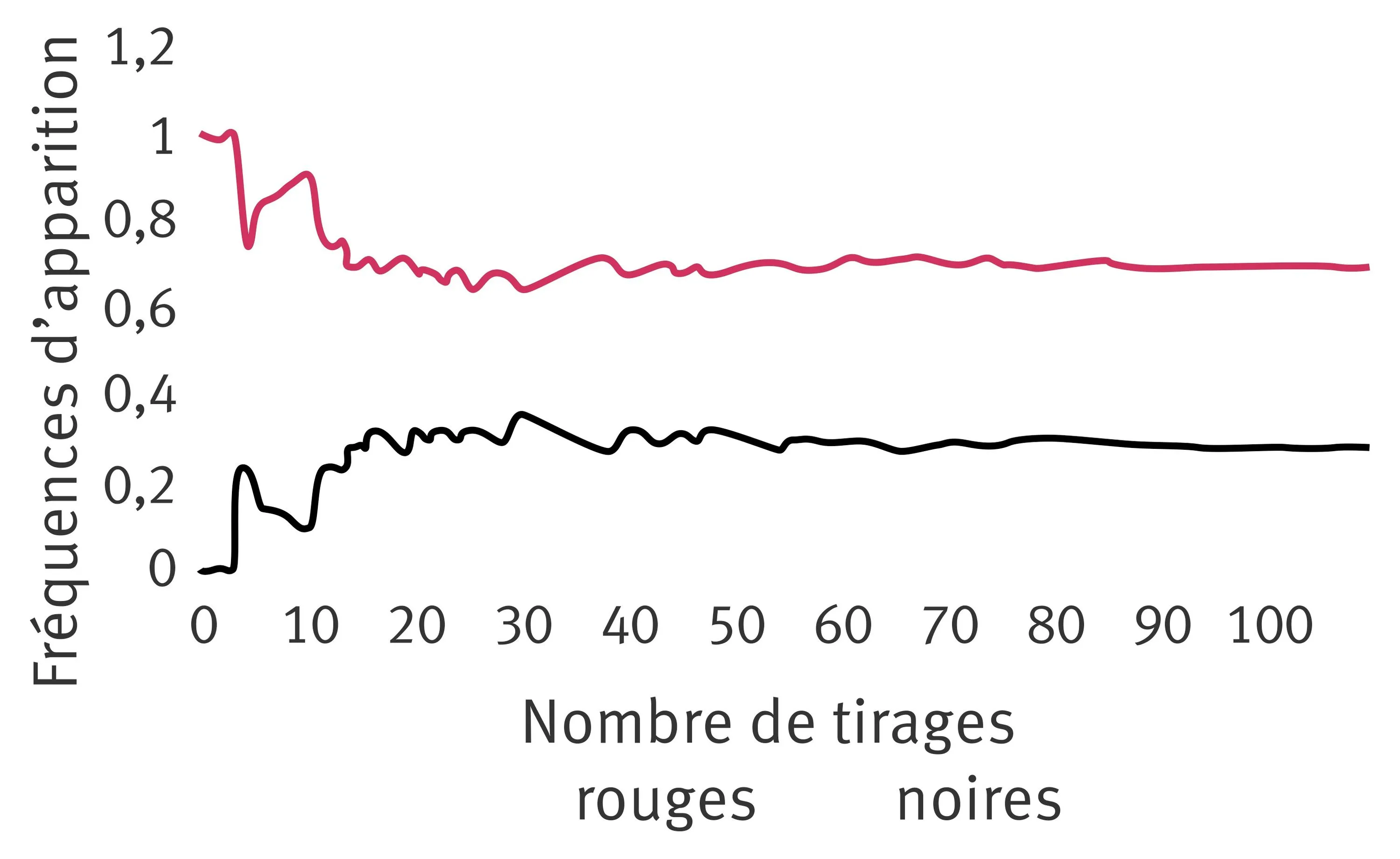
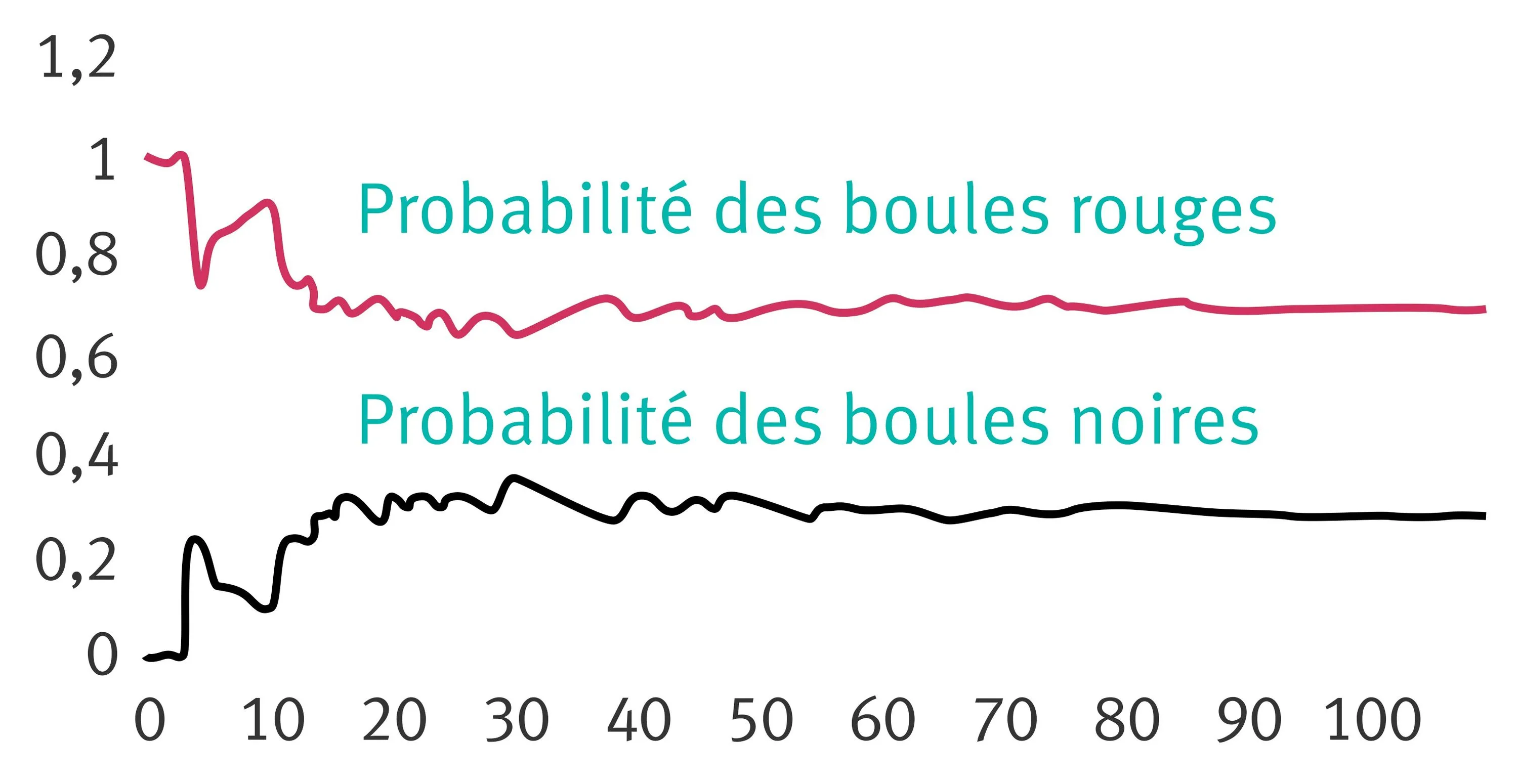
Dans une célèbre émission de télévision, deux équipes sʼaffrontent en cherchant des mots. À chaque mot trouvé, ils tirent une boule dans une urne. Il y a des boules rouges et six boules noires. Les fréquences des tirages sont représentées ci-contre en fonction du nombre de tirages.

a. Y a-t-il plus ou moins de boules rouges que de boules noires ? Aucune justification nʼest attendue.

b. On sait que la probabilité de tirer une boule noire est de 30 %. Combien y a-t-il de boules rouges dans lʼurne ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Comment faire le jour J ?

Question a. Pour comparer le nombre de boules, il suffit de comparer les probabilités. En effet, on aura plus de chances de tirer la couleur qui est en plus grand nombre. Faites une approximation des probabilités de chacun des tirages, en lisant le graphique donné. On utilise ici une interprétation fréquentiste des probabilités.

Question b. Écrivez les dfférentes formules liant les probabilités du problème sur votre brouillon. Puis remplacez les évènements et les nombres par ceux qui vous intéressent dans lʼexercice.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode

Quand un exercice vous propose un graphique, regardez en premier lieu ce quʼil représente, quelles sont ses abscisses et ses ordonnées.
Lʼénoncé est long et donne des informations qui ne sont pas utiles. Nʼhésitez pas à recopier au brouillon celles qui le sont, pour vous en servir comme base de travail.

Corrigé

a. Il y a plus de boules rouges que de boules noires dans lʼurne.
b.

\text{P}(\text{boule noire}) = \dfrac{\text{nombre boules noires}}{\text{nombre boules}} ;

\text{P}(\text{boule noire}) = \dfrac{30}{100} = \dfrac{6}{\text{nombre de boules}} ;

\text{Nombre de boules} = \dfrac{6 \times 100}{30} = 20.

Nombre de boules rouges \text{=} nombre total de boules \text{-} nombre de boules noires
Nombre de boules rouges \text{= 20 - 6 = 14}.

Il y a donc 14 boules rouges.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Oups, une coquille

j'ai une idée !

Nous préparons votre pageNous vous offrons 5 essais

Yolène

Émilie

Jean-Paul

Fatima

Sarah

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Problèmes corrigés

47 Jeu télévisé (Brevet Métropole, 2014)

Comment faire le jour J ?

Une erreur sur la page ? Une idée à proposer ?

Nous préparons votre pageNous vous offrons 5 essais

47
Jeu télévisé (Brevet Métropole, 2014)