Chapitre 3
Exercices
Suites numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calcul de terme de rang donné d'une suite géométrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 1
Calculer les cinq premiers termes de la suite géométrique (u_n) définie par u_{1}=1 et q = 1{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 2
Calculer les cinq premiers termes de la suite géométrique (v_n) définie par v_{0}=-8 et q=1{,}5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 3
Parmi les suites ci-dessous dont on donne les cinq premiers termes, déterminer celles pouvant être géométriques. Justifier.
1. 5 ; 10 ; 20 ; 40 ; 80
2. 2 ; 4 ; 6 ; 8 ; 10
3. 64 ; 16 ; 4 ; 1 ; 0,25
4. 1 ; 3 ; 9 ; 27 ; 54
5. –3 ; –30 ; –300 ; –3 000 ; –30 000
6. 50 ; 25 ; 12,5 ; 6,25 ; 3,125
1. 5 ; 10 ; 20 ; 40 ; 80
2. 2 ; 4 ; 6 ; 8 ; 10
3. 64 ; 16 ; 4 ; 1 ; 0,25
4. 1 ; 3 ; 9 ; 27 ; 54
5. –3 ; –30 ; –300 ; –3 000 ; –30 000
6. 50 ; 25 ; 12,5 ; 6,25 ; 3,125
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 4
On considère la suite (z_n) définie par son premier terme z_{1}=120 et par la relation de récurrence,
valable pour tout entier n, z_{n+1}=z_{n} \times 0{,}5 .
Calculer z_2, z_3 et z_4.
Calculer z_2, z_3 et z_4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 5
On considère une suite géométrique (w_n) de raison q = 2 telle que w_{3}=100.
Calculer w_1, w_4 et w_{10}.
Calculer w_1, w_4 et w_{10}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 6
On considère une suite géométrique (t_n) de premier terme t_{1}=3 et de raison q = 3.
Calculer t_{11}.
Calculer t_{11}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 7
On considère une suite géométrique (p_n) de premier terme p_{1}=5 et de troisième terme p_{3}=245.
Déterminer la raison q de cette suite.
Déterminer la raison q de cette suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Représentation graphique et sens de variation d'une suite géométrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 8
La représentation graphique ci-dessous du nuage de points \left(n\:; u_{n}\right) est celle d'une suite géométrique (u_n).

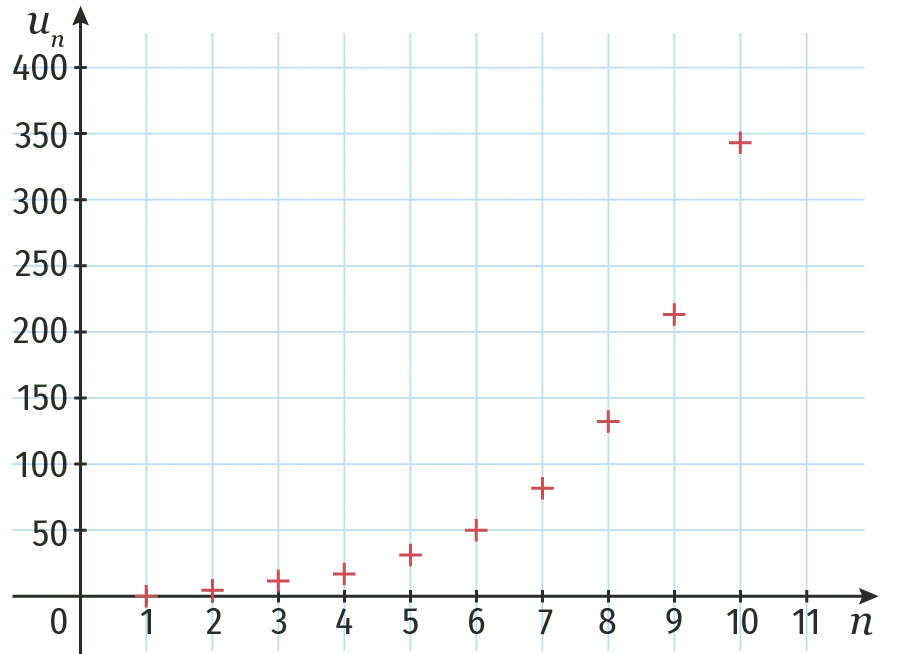
1. Préciser le sens de variation de cette suite.
2. Choisir la bonne réponse.


1. Préciser le sens de variation de cette suite.
2. Choisir la bonne réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 9
La représentation graphique ci-dessous du nuage de points \left(n\:; v_{n}\right) est celle d'une suite géométrique (v_n).

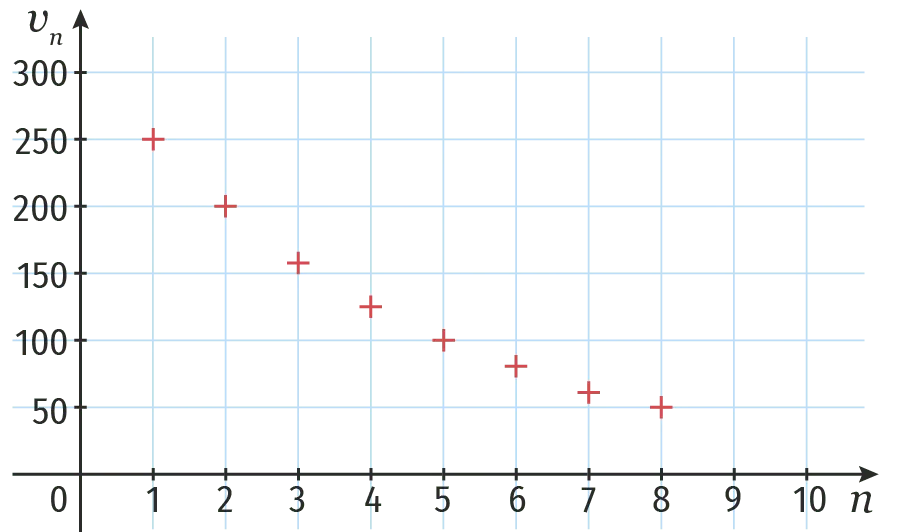
1. Préciser le sens de variation de cette suite.
2. Choisir la bonne réponse.


1. Préciser le sens de variation de cette suite.
2. Choisir la bonne réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 10
Indiquer le sens de variation de chacune des suites.
1. u_{n}=0{,}1 \times 2^{n}
2. v_{n}=-5 \times 0{,}1^{n}
3. t_{n}=2 \times 0{,}2^{n}
4. w_{n}=3 \times 4^{n}
1. u_{n}=0{,}1 \times 2^{n}
2. v_{n}=-5 \times 0{,}1^{n}
3. t_{n}=2 \times 0{,}2^{n}
4. w_{n}=3 \times 4^{n}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 11
Associer chacune des suites à la représentation graphique du nuage de points correspondant.

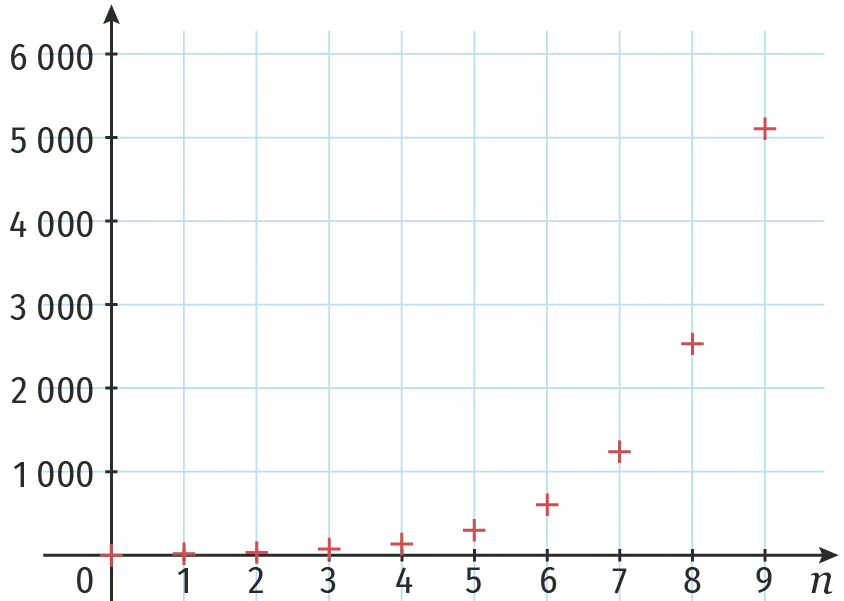
1.

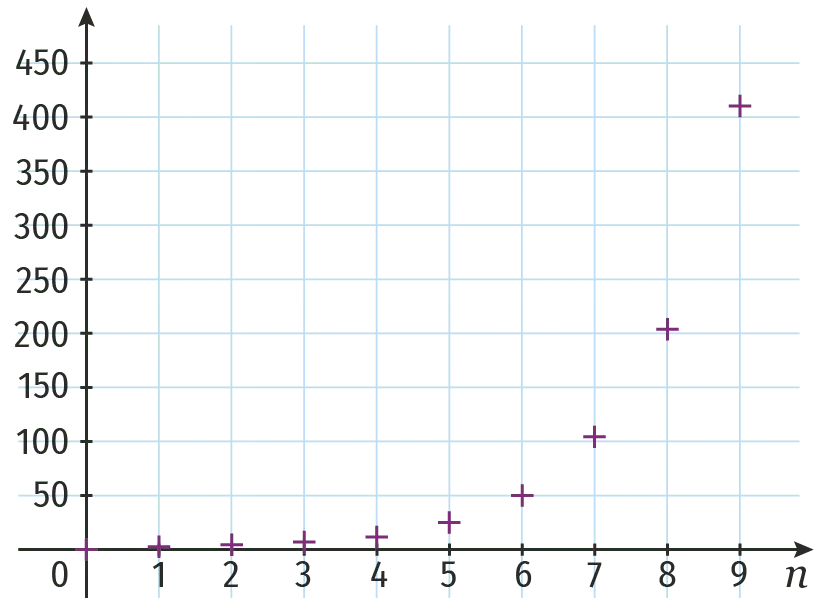
2.

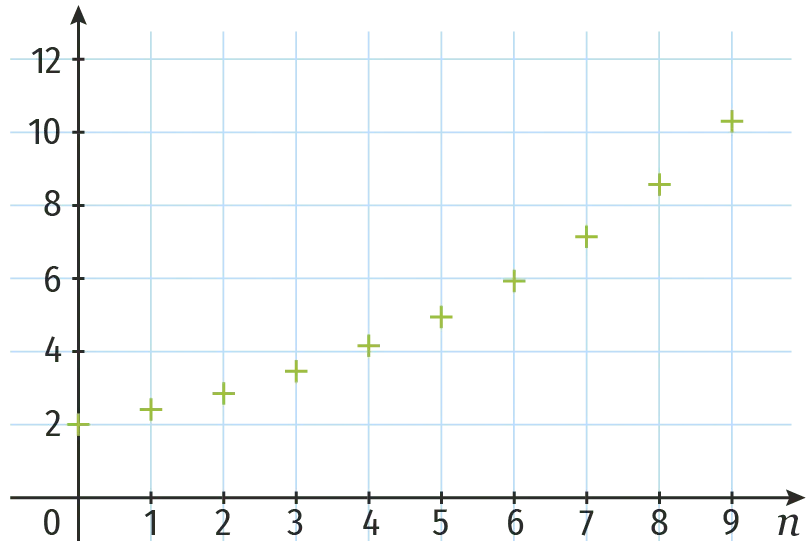
3.

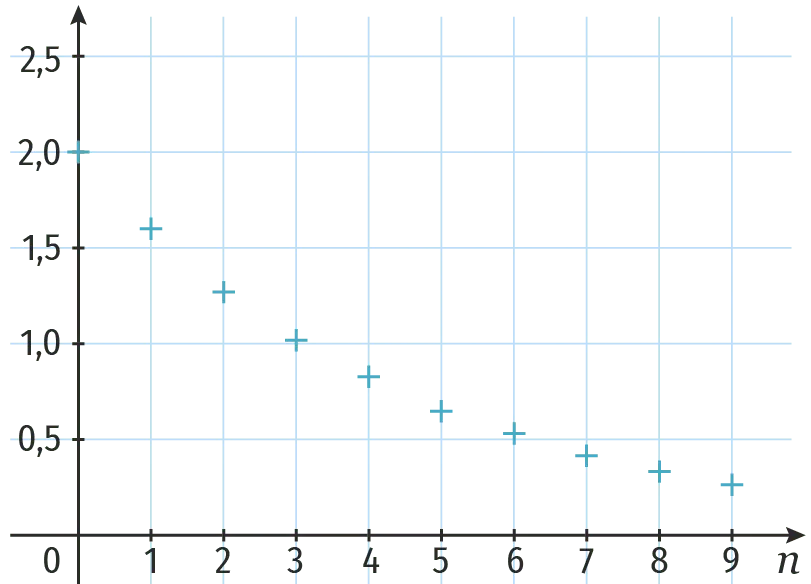
4.


1.


2.


3.


4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calcul de la somme des n premiers termes d'une suite géométrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 12
Algorithmique
Le programme suivant permet de calculer la somme des termes d'une suite géométrique.
1. Donner le premier terme et la raison de cette suite géométrique.
2. Indiquer la valeur obtenue si on lance le programme en inscrivant somme(3).
def somme(n) :
u = 2
s = 0
for i in range(n):
s = s + u
u = 3*u
return (s)
1. Donner le premier terme et la raison de cette suite géométrique.
2. Indiquer la valeur obtenue si on lance le programme en inscrivant somme(3).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 13
Algorithmique
Pour calculer le terme un d'une suite géométrique (u_n) de premier terme u_0 et de raison q, Sonia a écrit la fonction terme ci-dessous.
1. Son programme ne donne pas le bon résultat. Quelle erreur a-t-elle commise ?
2. Comment Sonia doit-elle compléter la fonction somme pour que celle-ci renvoie la somme des n premiers termes de la suite ?
def terme (u0, q, n): un = u0*q**(n-1) return(un) def somme (u0, q, n): somme = ... return(somme)
1. Son programme ne donne pas le bon résultat. Quelle erreur a-t-elle commise ?
2. Comment Sonia doit-elle compléter la fonction somme pour que celle-ci renvoie la somme des n premiers termes de la suite ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 14
On considère la suite géométrique (v_n) de premier terme v_{3}=50 et de raison q = 5.
Calculer la valeur de la somme v_{3}+v_{4}+v_{5}+v_{6}.
Calculer la valeur de la somme v_{3}+v_{4}+v_{5}+v_{6}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 15
On considère la suite géométrique (u_n) de premier terme u_{1}=5 et de raison q = 3.
Calculer la valeur de la somme des dix premiers termes de cette suite.
Calculer la valeur de la somme des dix premiers termes de cette suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Bilan
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 16
Les caractéristiques des formats des feuilles rectangulaires utilisées en imprimerie A0, A1, A2, etc. sont partiellement données dans le tableau ci-dessous.

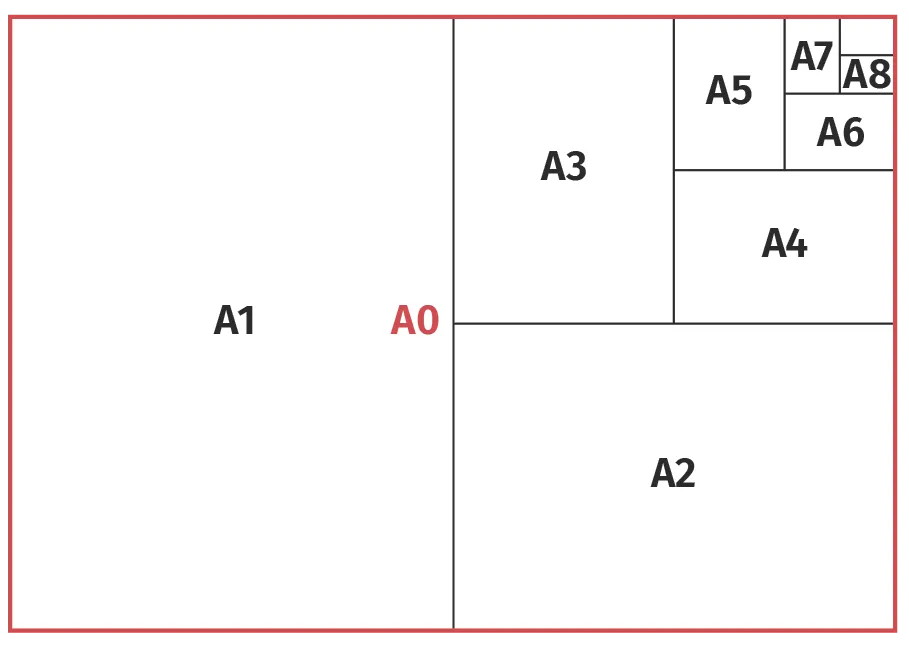
1.a. Les longueurs \text{L}_0, \text{L}_1, \text{L}_2, etc. forment une suite géométrique de raison q=\frac{\sqrt{2}}{2}.
Calculer \text{L}_0, \text{L}_2 et \text{L}_3 (résultats arrondis à 0,1).
1.b. Reporter les résultats obtenus dans le .
2. Les largeurs l_0, l_1, l_2, etc. forment également une suite géométrique de raison q=\frac{\sqrt{2}}{2}.
Calculer l_0, l_2 et l_3 (résultats arrondis à 0,1) puis reporter les résultats dans .
3. Calculer les surfaces \text{S}_0, \text{S}_1, \text{S}_2, \text{S}_3 et \text{S}_4 des feuilles de formats A0, A1, A2, A3, A4 puis reporter les résultats dans .
4. Indiquer si ces surfaces forment une suite arithmétique ou une suite géométrique puis préciser la raison.

 5.
Le timbre poste « Marianne » a pour format A11. Calculer les dimensions \text{L}_{11} et l_{11} d'un timbre-poste « Marianne ».
5.
Le timbre poste « Marianne » a pour format A11. Calculer les dimensions \text{L}_{11} et l_{11} d'un timbre-poste « Marianne ».
| Format | A0 | A1 | A2 | A3 | A4 |
| Longueur \text{L}_n en cm | 84 | 29,7 | |||
| Largeur l_n en cm | 59,4 | 21 | |||
| Surface \text{S}_n en cm2 |


1.a. Les longueurs \text{L}_0, \text{L}_1, \text{L}_2, etc. forment une suite géométrique de raison q=\frac{\sqrt{2}}{2}.
Calculer \text{L}_0, \text{L}_2 et \text{L}_3 (résultats arrondis à 0,1).
1.b. Reporter les résultats obtenus dans le .
2. Les largeurs l_0, l_1, l_2, etc. forment également une suite géométrique de raison q=\frac{\sqrt{2}}{2}.
Calculer l_0, l_2 et l_3 (résultats arrondis à 0,1) puis reporter les résultats dans .
3. Calculer les surfaces \text{S}_0, \text{S}_1, \text{S}_2, \text{S}_3 et \text{S}_4 des feuilles de formats A0, A1, A2, A3, A4 puis reporter les résultats dans .
4. Indiquer si ces surfaces forment une suite arithmétique ou une suite géométrique puis préciser la raison.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 17
Murielle rembourse une dette en cinq ans. Elle effectue un remboursement à la fin de chaque année. Les remboursements forment une suite géométrique de raison 1,2.
1. Le dernier versement s'élève à 2 073,60 €. Déterminer le montant de chacun des remboursements.
2. Calculer le montant de la dette.
1. Le dernier versement s'élève à 2 073,60 €. Déterminer le montant de chacun des remboursements.
2. Calculer le montant de la dette.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 18
Une bactérie se multiplie par fission binaire : la bactérie « mère » se divise en deux bactéries « filles » identiques l'une à l'autre. Chaque nouvelle bactérie reproduit ensuite le même processus comme indiqué sur le schéma ci-dessous.

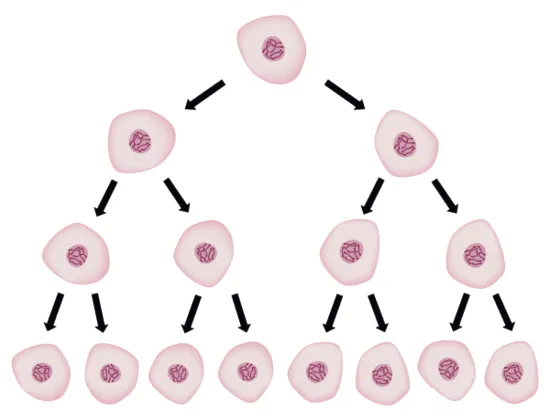
Le temps nécessaire à une division est de vingt minutes. Calculer le nombre de bactéries obtenues à partir d'une bactérie « mère » en 1 h, 2 h, 3 h et en 12 h.


Le temps nécessaire à une division est de vingt minutes. Calculer le nombre de bactéries obtenues à partir d'une bactérie « mère » en 1 h, 2 h, 3 h et en 12 h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice 19
D'après une légende, le sage Sissa aurait demandé au roi Indien Belkib, comme récompense pour avoir inventé le jeu d᾽échecs, un peu de riz réparti de la manière suivante : un grain sur la première case de l'échiquier, deux grains sur la deuxième, quatre grains sur la troisième, huit grains sur la quatrième et ainsi de suite jusqu'à la 64e case. Le roi Belkib, trouvant cette récompense très raisonnable, accepta sans hésitation.
On note u_n le nombre de grains de riz posés sur la ne case de l'échiquier.
La suite (u_n) est une suite géométrique.
1. Indiquer le premier terme u_1 et la raison q de cette suite.
2. Calculer la quantité de grains de riz demandée par Sissa en récompense.
3. Comparer cette quantité à la production annuelle mondiale de riz à l'aide d'une recherche Internet.
4. Le roi Belkib a-t-il pu honorer sa parole ?
On note u_n le nombre de grains de riz posés sur la ne case de l'échiquier.
La suite (u_n) est une suite géométrique.
1. Indiquer le premier terme u_1 et la raison q de cette suite.
2. Calculer la quantité de grains de riz demandée par Sissa en récompense.
3. Comparer cette quantité à la production annuelle mondiale de riz à l'aide d'une recherche Internet.
4. Le roi Belkib a-t-il pu honorer sa parole ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

