Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Partie 1 : Statistique et probabilités
Ch. 1
Statistiques à deux variables
Ch. 2
Probabilités
Partie 2 : Algèbre - Analyse
Ch. 3
Suites numériques
Ch. 4
Fonctions polynômes de degré 3
Ch. 5
Fonctions exponentielles et logarithme décimal
Ch. 6
Calculs commerciaux et financiers
Partie 3 : Géométrie
Ch. 7
Vecteurs
Ch. 8
Trigonométrie
Annexes
Révisions Genially
Consolidation
Poursuite d'études
Annexes
Programmation
Cahier d'algorithmique et de programmation
Chapitre 8
Applications directes
Trigonométrie
17 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Déterminer et tracer le vecteur de Fresnel d'une grandeur sinusoïdale.
| Grandeur sinusoïdale | Vecteur de Fresnel | Représentation graphique |
|---|---|---|
| u(t)=\mathrm{U} \sin (\omega t+\varphi) | \vec{u}(\mathrm{U} \: ; \varphi) |  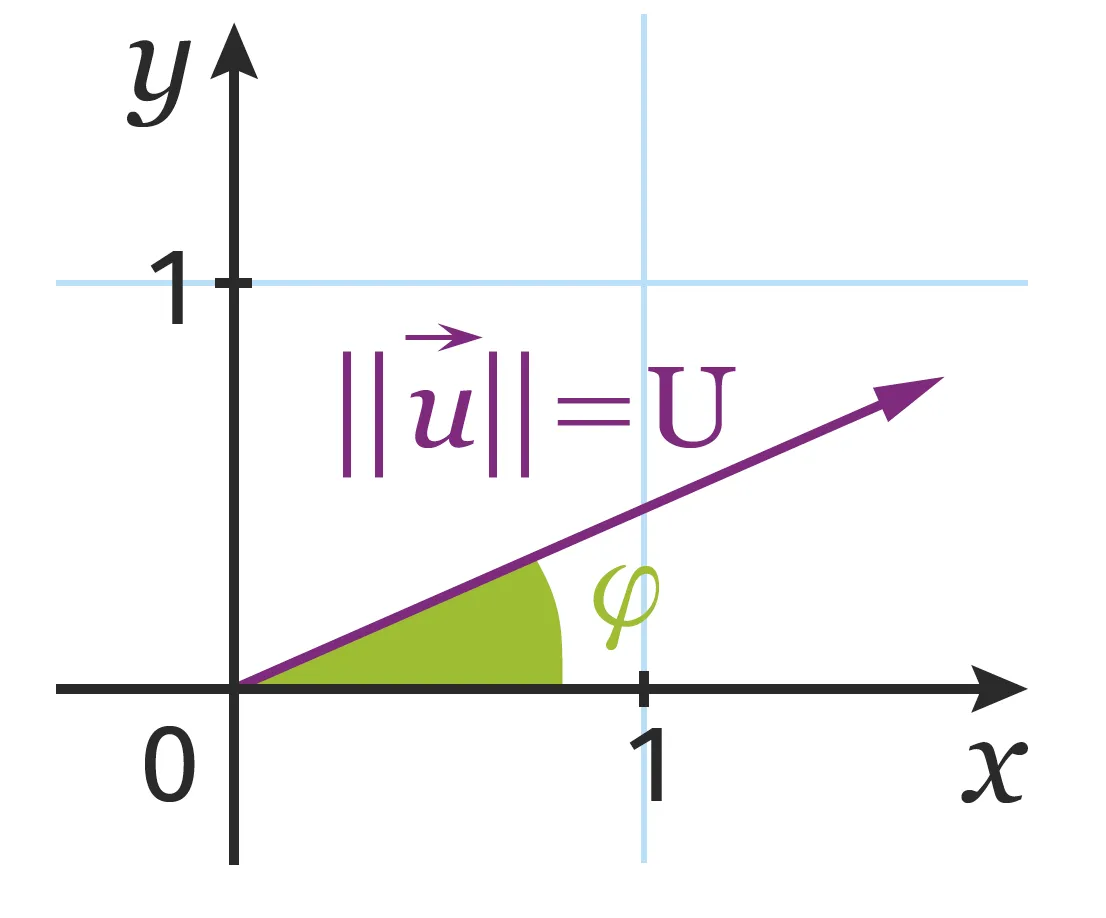 Le zoom est accessible dans la version Premium. |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résoudre une équation de type \bm{\cos(x)=a} et \bm{\sin(x)=a} sur \bm{]-\pi \: ; \pi]}.
1. Dans ce type d'équation, l'inconnue est x.
2. Vérifier que a appartient bien à [-1 \: ; 1] : si ce n'est pas le cas, l'équation n'admet aucune solution.
3. Si a appartient à [-1 \: ; 1], placer sur le cercle trigonométrique, suivant la situation, les points admettant un cosinus ou un sinus égal à a.
4. Si a est une valeur remarquable, déterminer les solutions grâce à un tableau de valeurs remarquables. Si a n'est pas une valeur remarquable, utiliser la calculatrice pour déterminer une valeur approchée de \cos ^{-1}(a) ou \sin ^{-1}(a).
2. Vérifier que a appartient bien à [-1 \: ; 1] : si ce n'est pas le cas, l'équation n'admet aucune solution.
3. Si a appartient à [-1 \: ; 1], placer sur le cercle trigonométrique, suivant la situation, les points admettant un cosinus ou un sinus égal à a.
4. Si a est une valeur remarquable, déterminer les solutions grâce à un tableau de valeurs remarquables. Si a n'est pas une valeur remarquable, utiliser la calculatrice pour déterminer une valeur approchée de \cos ^{-1}(a) ou \sin ^{-1}(a).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résoudre une équation de type \bm{\sin (\omega t+\varphi)=a}.
1. Dans ce type d'équation, l'inconnue est t.
2. Utiliser la méthode de résolution d'une équation de type \sin(x) = a pour déterminer les valeurs possibles de \omega t+\varphi. On obtient une ou plusieurs solutions x_i.
3. Résoudre chacune des équations \omega t+\varphi = x_i pour obtenir la ou les valeurs de t.
2. Utiliser la méthode de résolution d'une équation de type \sin(x) = a pour déterminer les valeurs possibles de \omega t+\varphi. On obtient une ou plusieurs solutions x_i.
3. Résoudre chacune des équations \omega t+\varphi = x_i pour obtenir la ou les valeurs de t.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
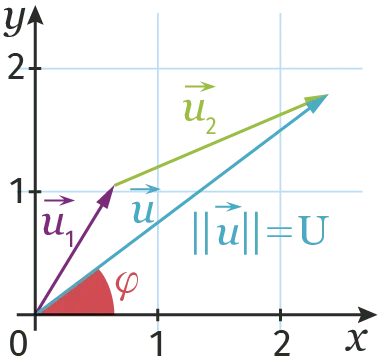
Additionner deux grandeurs sinusoïdales de même fréquence en utilisant les vecteurs de Fresnel.
Pour déterminer une expression de u=u_{1}+u_{2}, où u_1 et u_2 sont deux grandeurs sinusoïdales de même fréquence f, il faut :
1. tracer, dans un même repère, \overrightarrow{u_1} et \overrightarrow{u_2}, les vecteurs de Fresnel associés à u_1 et u_2 ;
2. tracer dans ce repère le vecteur \vec{u}=\overrightarrow{u_{1}}+\overrightarrow{u_{2}} ;
3. mesurer la norme \text{U} de \overrightarrow{u} et l'angle \varphi entre l'axe des abscisses et le vecteur \overrightarrow{u} ;
4. la grandeur u a pour expression u(t)=\mathrm{U}(\omega t+\varphi) où \omega=2 \pi f.
1. tracer, dans un même repère, \overrightarrow{u_1} et \overrightarrow{u_2}, les vecteurs de Fresnel associés à u_1 et u_2 ;
2. tracer dans ce repère le vecteur \vec{u}=\overrightarrow{u_{1}}+\overrightarrow{u_{2}} ;
3. mesurer la norme \text{U} de \overrightarrow{u} et l'angle \varphi entre l'axe des abscisses et le vecteur \overrightarrow{u} ;
4. la grandeur u a pour expression u(t)=\mathrm{U}(\omega t+\varphi) où \omega=2 \pi f.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Mise en pratique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
QCM
Une ou plusieurs bonnes réponses possibles.
1. Soit l'intensité i(t)=4 \sin \left(314 t+\frac{\pi}{2}\right). Quelle est la valeur de i à t = 0 ?
2. Soit l'intensité i(t)=4 \sin \left(314 t+\frac{\pi}{2}\right). Quel est le vecteur de Fresnel qui lui est associé ?
3. Sur l'intervalle ]-\pi \: ; \pi], l'équation \cos(x) = 0 admet comme solution :
4. Sur l'intervalle ]-\pi \: ; \pi] l'équation \sin (x)=\frac{1}{2} admet comme solution :
2. Soit l'intensité i(t)=4 \sin \left(314 t+\frac{\pi}{2}\right). Quel est le vecteur de Fresnel qui lui est associé ?
3. Sur l'intervalle ]-\pi \: ; \pi], l'équation \cos(x) = 0 admet comme solution :
4. Sur l'intervalle ]-\pi \: ; \pi] l'équation \sin (x)=\frac{1}{2} admet comme solution :
5. Soit \overrightarrow{\mathrm{OM}}(5 \: ; 4), un vecteur de Fresnel associé à une fonction f. Quelle pourrait être l'expression de cette fonction f ?
6. Une tension sinusoïdale u de fréquence 50 Hz et de valeur maximale 230 V est prise comme origine des phases (sa phase à l'origine est nulle). Comment s'écrit‑elle en fonction du temps t en seconde ?
7. Quel est le nombre de solutions à l'équation \cos(x)=0,3 sur ]-\pi \: ; \pi] ?
8. Quelles sont les solutions de l'équation \cos(x)=0,3 sur ]-\pi \: ; \pi] ?
9. Quel est le nombre de solutions de l'équation 0,2 \sin \left(314 x+\frac{\pi}{4}\right)=1 sur ]-\pi \: ; \pi] ?
6. Une tension sinusoïdale u de fréquence 50 Hz et de valeur maximale 230 V est prise comme origine des phases (sa phase à l'origine est nulle). Comment s'écrit‑elle en fonction du temps t en seconde ?
7. Quel est le nombre de solutions à l'équation \cos(x)=0,3 sur ]-\pi \: ; \pi] ?
8. Quelles sont les solutions de l'équation \cos(x)=0,3 sur ]-\pi \: ; \pi] ?
9. Quel est le nombre de solutions de l'équation 0,2 \sin \left(314 x+\frac{\pi}{4}\right)=1 sur ]-\pi \: ; \pi] ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème
Un électricien souhaite alimenter un circuit avec un courant d'intensité sinusoïdale d'expression {i_{3}(t)=5 \sin \left(\pi t+\frac{5 \pi}{18}\right)}. Pour ce faire, il souhaite utiliser deux courants sinusoïdaux : un d'intensité i_{1}(t)=3 \sin (\pi t) et un autre d'intensité i_2 qu'il cherche à déterminer.
Problématique
Déterminer une expression de l'intensité \bm{i_2} que l'électricien doit utiliser.
2. Tracer sur un même graphique les vecteurs de Fresnel \overrightarrow{i_1} et \overrightarrow{i_3} des grandeurs i_1 et i_3.
GeoGebra
3. Tracer le vecteur \overrightarrow{i_2} tel que \overrightarrow{i_{3}}=\overrightarrow{i_{1}}+\vec{i}_{2}.
4. Donner une expression possible de la grandeur i_2 représentée par le vecteur de Fresnel \overrightarrow{i_2} précédent.
5. Répondre à la problématique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Réviser les notions de ce chapitre grâce à cette activité interactive.
Pour une utilisation optimale, réaliser l'activité en plein écran.
Genially
Pour une utilisation optimale, réaliser l'activité en plein écran.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah