Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Exercices rituels et automatismes
Exercices rituels
Automatismes
Partie 1 - Information chiffrée
Ch. 1
Analyse de l'information chiffrée
Partie 2 - Probabilités
Ch. 2
De la statistique aux probabilités
Partie 3 - Phénomènes d’évolution
Ch. 3
Croissance linéaire
Ch. 4
Croissance exponentielle
Partie 4 - Dérivation
Ch. 5
Variations instantanées
Ch. 6
Variations globales
GeoGebra
Chapitre 4
Cours
Croissance exponentielle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Suites géométriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADéfinition
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Une suite u est géométrique lorsqu'il existe un nombre réel q, nommé raison, tel que pour tout entier naturel n : u(n+1)=q \times u(n).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans ce chapitre, on se limite au cas où u(0)>0 et q>0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La suite u définie par u(0)=8 et, pour tout entier naturel n, u(n+1)=0,5 \times u(n) est une suite géométrique de premier terme 8 et de raison q=0,5.
On a u(0)=8, u(1)=0,5 \times u(0)=4, u(2)=0,5 \times u(1)=2, etc.
On a u(0)=8, u(1)=0,5 \times u(0)=4, u(2)=0,5 \times u(1)=2, etc.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Si u est une suite géométrique de raison q et de premier terme u(0), alors pour tout entier naturel n : u(n)=u(0) \times q^{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit u la suite géométrique définie par u(0)=10 et vérifiant, pour tout entier naturel n, u(n+1)=8 \times u(n). On en déduit que, pour tout entier naturel n, u(n)=10 \times 8^{n}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BSens de variation d'une suite géométrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Une suite géométrique u de premier terme u(0)>0 et de raison q>0 est :
- strictement croissante si, et seulement si, q>1 ;
- strictement décroissante si, et seulement si, 0 < q < 1 ;
- constante si, et seulement si, q=1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
-
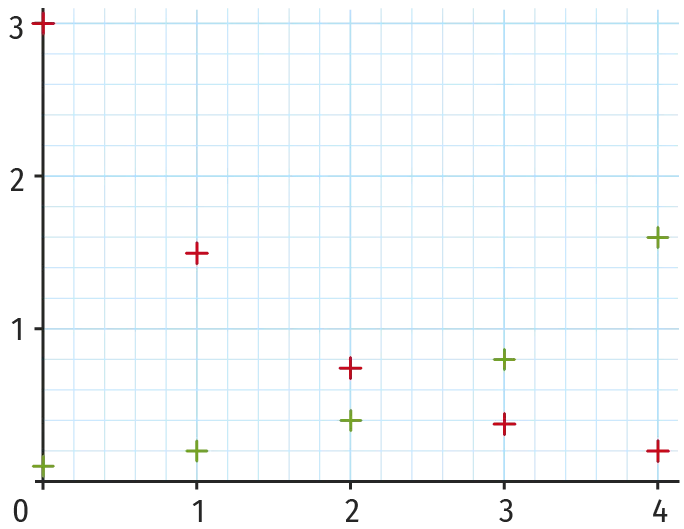
En rouge : Nuage de points associé à la suite géométrique u de premier terme u(0)=3 et de raison q=0,5.
On a 0 < 0,5 < 1 donc la suite u est décroissante.
Cela se vérifie avec les premiers termes : u(0)=3, u(1)=1,5, u(2)=0,75, etc.
-
En vert : Nuage de points associé à la suite géométrique v de premier terme v(0)=0,1 et de raison q=2.
Ici, on a 2>1 donc la suite v est croissante.
Cela se vérifie avec les premiers termes : v(0)=0,1, v(1)=0,2, v(2)=0,4, etc.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Fonctions exponentielles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADéfinition et variations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Soit \mathrm{a} un réel strictement positif. Une fonction \mathrm{f} définie pour tout réel x \in[0 ;+\infty[ par f(x)=a^{x} est une fonction exponentielle.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Une fonction exponentielle f définie sur [\;0\; ;+\infty[ par f(x)=a^{x} avec a>0 est :
1. strictement croissante sur [0 ;+\infty[ si, et seulement si, a>1 ;
2. strictement décroissante sur [0 ;+\infty[ si, et seulement si, 0 < a < 1 ;
3. constante sur [0 ;+\infty[ si, et seulement si, a = 1.
1. strictement croissante sur [0 ;+\infty[ si, et seulement si, a>1 ;
2. strictement décroissante sur [0 ;+\infty[ si, et seulement si, 0 < a < 1 ;
3. constante sur [0 ;+\infty[ si, et seulement si, a = 1.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BPropriétés algébriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Pour tous réels positifs x et y et pour tours réels strictement positifs a et b on a :
1.a^{x} \times a^{y}=a^{x+y}
2.\frac{a^{x}}{a^{y}}=a^{x-y} (avec x \geqslant y)
3.\left(a^{x}\right)^{y}=a^{x \times y}
4.a^{x} \times b^{x}=(a \times b)^{x}
5.\frac{a^{x}}{b^{x}}=\left(\frac{a}{b}\right)^{x}
1.a^{x} \times a^{y}=a^{x+y}
2.\frac{a^{x}}{a^{y}}=a^{x-y} (avec x \geqslant y)
3.\left(a^{x}\right)^{y}=a^{x \times y}
4.a^{x} \times b^{x}=(a \times b)^{x}
5.\frac{a^{x}}{b^{x}}=\left(\frac{a}{b}\right)^{x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Cas particulier de la puissance \boldsymbol{\frac{1}{n}}
Soit a et x deux nombres réels strictement positifs et n un nombre entier non nul. L'équation x^{n}=a admet comme unique solution positive le réel x=\sqrt[n]{a}=a ^ {\normalsize{\tfrac{1}{n}}} appelé racine \boldsymbol{n} -ième de a.
Soit a et x deux nombres réels strictement positifs et n un nombre entier non nul. L'équation x^{n}=a admet comme unique solution positive le réel x=\sqrt[n]{a}=a ^ {\normalsize{\tfrac{1}{n}}} appelé racine \boldsymbol{n} -ième de a.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriétés
Si une grandeur subit une évolution de taux t, alors elle atteint la même valeur en subissant n évolutions successives de même taux (1+t)^{\normalsize{\tfrac{1}{n}}} où n est un entier naturel non nul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
Le nombre (1+t)^{\normalsize{\tfrac{1}{n}}}-1 est appelé taux moyen des n évolutions successives de taux global t.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
D'après l'association 60 Millions de consommateurs, le prix des pâtes a augmenté d'environ 11,4 % entre février 2021 et février 2022.
t_{\text {moyen }}=\left(1+\frac{11,4}{100}\right)^{\normalsize{\tfrac{1}{12}}}-1 \approx 0,00904 \approx 0,904 \%.
En moyenne, entre février 2021 et février 2022, le prix des pâtes a augmenté de 0,904 % par mois.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah