Chapitre 11
Cours
Décrire un mouvement
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Système et référentiel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASystème
La cinématique est l'étude purement descriptive du mouvement d'un système. On ne s'intéresse alors pas aux causes du mouvement.
Le système est l'objet ou un ensemble d'objets reliés entre eux, dont on étudie le mouvement. Pour simplifier l'étude, on modélise le système par un point, de même masse, et situé au centre de gravité de l'objet. C'est le modèle du point matériel.
Le modèle du point matériel ne prend en compte ni la géométrie de l'objet, ni ses éventuelles déformations ou rotations. Il permet toutefois de décrire le déplacement global de cet objet.
Le système est l'objet ou un ensemble d'objets reliés entre eux, dont on étudie le mouvement. Pour simplifier l'étude, on modélise le système par un point, de même masse, et situé au centre de gravité de l'objet. C'est le modèle du point matériel.
Le modèle du point matériel ne prend en compte ni la géométrie de l'objet, ni ses éventuelles déformations ou rotations. Il permet toutefois de décrire le déplacement global de cet objet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Référentiel
Le référentiel d'étude est l'objet de référence par rapport auquel on étudie le mouvement du système (doc. 1).
On associe au référentiel un repère d'espace et un repère de temps.
Le repère d'espace doit être constitué de trois axes pour un mouvement à trois dimensions ou deux axes pour un mouvement à deux dimensions. Dans un repère cartésien à deux dimensions, le système assimilé à un point matériel \text{M} a pour coordonnées \text{M} (x ; y).
Un repère de temps est une horloge que tous les observateurs déclenchent en même temps.
On associe au référentiel un repère d'espace et un repère de temps.
Le repère d'espace doit être constitué de trois axes pour un mouvement à trois dimensions ou deux axes pour un mouvement à deux dimensions. Dans un repère cartésien à deux dimensions, le système assimilé à un point matériel \text{M} a pour coordonnées \text{M} (x ; y).
Un repère de temps est une horloge que tous les observateurs déclenchent en même temps.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Deux référentiels différents

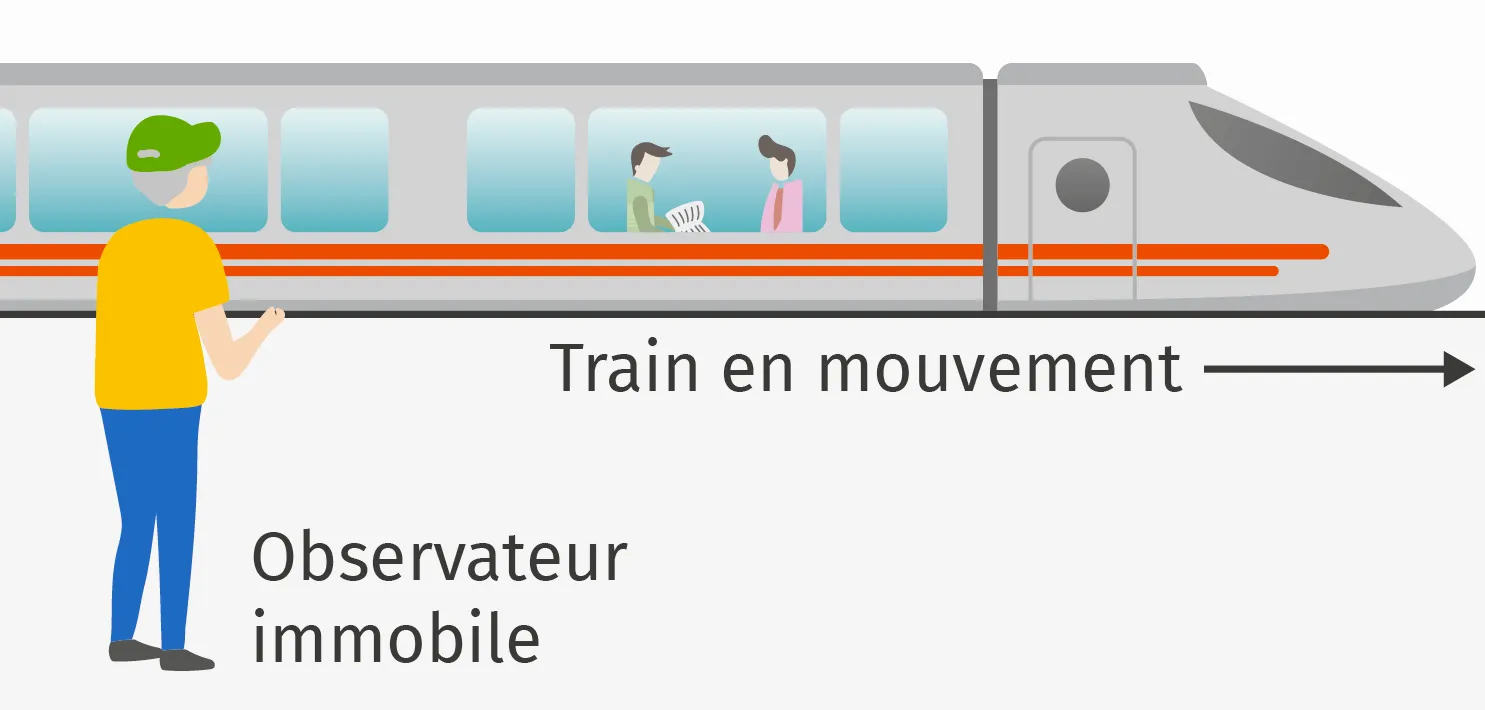
Voici deux référentiels distincts pour l'étude d'un mouvement : le référentiel terrestre et celui du train en marche.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Relativité du mouvement
La description du mouvement dépend du référentiel d'étude choisi.
Exemple : un voyageur lit, assis à bord d'un TGV en marche, et un passager se situe sur le quai (doc. 1). Dans le référentiel lié au passager situé sur le quai, le lecteur s'éloigne.
Dans le référentiel lié au voyageur assis face au lecteur, le lecteur est immobile. La notion de mouvement est donc relative au choix du référentiel d'étude.
Exemple : un voyageur lit, assis à bord d'un TGV en marche, et un passager se situe sur le quai (doc. 1). Dans le référentiel lié au passager situé sur le quai, le lecteur s'éloigne.
Dans le référentiel lié au voyageur assis face au lecteur, le lecteur est immobile. La notion de mouvement est donc relative au choix du référentiel d'étude.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Trajectoire et vecteur vitesse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ATrajectoire
La trajectoire d'un point matériel, dans un référentiel d'étude
donné, correspond à la courbe formée par l'ensemble des positions successivement occupées par le point matériel lors de son mouvement (doc. 2).
- Si la trajectoire est une droite, on dit que le mouvement est rectiligne (doc. 3).
- Si la trajectoire est un cercle ou une portion de cercle, on dit que le mouvement est circulaire.
- Si la trajectoire est une courbe quelconque, on dit que le mouvement est curviligne.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVecteur vitesse
Le vecteur vitesse d'un point matériel \text{M} permet de décrire la direction, le sens et la valeur de la vitesse en un point, à un instant t donné. Il est, en tout point, tangent à la trajectoire, et orienté dans le sens du mouvement.
Soient \text{M} la position d'un point matériel à la date t et \text{M}^{\prime} la position de ce même point à la date t^{\prime}. Le déplacement du point matériel entre les dates t et t^{\prime} par le vecteur de déplacement \overrightarrow{\mathrm{MM}^{\prime}}.
Pour obtenir la vitesse instantanée du point matériel \text{M} à la date t, il faut connaître sa position à une date \text{t}^{\prime} très proche de t. On calcule alors le vecteur vitesse instantanée :
En pratique, on ne peut pas mesurer la position d'un point à deux instants infiniment proches, séparés d'une durée \Delta t infiniment petite.
On mesure alors la vitesse moyenne entre deux points.
Le vecteur vitesse moyenne \vec{v}_{2} d'un système au point \text{M}_{2}, entre deux dates t_{1} et t_{3}, a pour expression :
Ce vecteur a les caractéristiques suivantes :
• t_{3}-t_{1} la durée séparant les instants t_{1} et t_{3} en seconde (s),
• v_{2} la valeur de la vitesse en mètre par seconde m\cdots-1.
En classe de seconde, on appellera vecteur vitesse le vecteur vitesse moyenne calculé entre deux points.
Soient \text{M} la position d'un point matériel à la date t et \text{M}^{\prime} la position de ce même point à la date t^{\prime}. Le déplacement du point matériel entre les dates t et t^{\prime} par le vecteur de déplacement \overrightarrow{\mathrm{MM}^{\prime}}.
Pour obtenir la vitesse instantanée du point matériel \text{M} à la date t, il faut connaître sa position à une date \text{t}^{\prime} très proche de t. On calcule alors le vecteur vitesse instantanée :
\vec{v}=\dfrac{\overrightarrow{\text{M}\text{M}^{\prime}}}{\Delta t} avec {\Delta t}=t^{\prime}-t
En pratique, on ne peut pas mesurer la position d'un point à deux instants infiniment proches, séparés d'une durée \Delta t infiniment petite.
On mesure alors la vitesse moyenne entre deux points.
Le vecteur vitesse moyenne \vec{v}_{2} d'un système au point \text{M}_{2}, entre deux dates t_{1} et t_{3}, a pour expression :
\vec{v}_{2}=\dfrac{\overrightarrow{\text{M}_{1} \text{M}_{3}}}{t_{3}-t_{1}}
Ce vecteur a les caractéristiques suivantes :
- direction : parallèle au segment \text{M}_{1} \text{M}_{3};
- sens : celui du mouvement ;
- norme : v_{2}=\dfrac{\mathrm{M}_{1} \mathrm{M}_{3}}{t_{3}-t_{1}} avec :
• t_{3}-t_{1} la durée séparant les instants t_{1} et t_{3} en seconde (s),
• v_{2} la valeur de la vitesse en mètre par seconde m\cdots-1.
En classe de seconde, on appellera vecteur vitesse le vecteur vitesse moyenne calculé entre deux points.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application
Tracer le vecteur vitesse au point \mathrm{\text{M}}_{2} (doc. 4), la durée entre deux marquages étant de 50 ms.
1. Mesurer la distance réelle entre les points \text{M}_{1} et \text{M}_{3}. En tenant compte de l'échelle indiquée : \text{M}_{1} \text{M}_{3}= 72\text{,}5 cm. On en déduit la valeur de la vitesse
v_{2}=\dfrac{\mathrm{M}_{1} \mathrm{M}_{3}}{t_{3}-t_{1}}=\dfrac{\mathrm{M}_{1} \mathrm{M}_{3}}{2 \tau}=\dfrac{72\text{,}5 \times 10^{-2}}{2 \times 50 \times 10^{-3}}= 7\text{,}3 m\cdots-1
2. Choisir une échelle de représentation des vitesses (voir doc. 4). En fonction de l'échelle choisie, tracer le vecteur vitesse \vec{v}_{2} parallèle au segment \mathrm{M}_{1} \mathrm{M}_{3}, partant de \text{M}_{2} et d'une longueur adaptée à l'échelle qui a été choisie.
Corrigé
1. Mesurer la distance réelle entre les points \text{M}_{1} et \text{M}_{3}. En tenant compte de l'échelle indiquée : \text{M}_{1} \text{M}_{3}= 72\text{,}5 cm. On en déduit la valeur de la vitesse
v_{2}=\dfrac{\mathrm{M}_{1} \mathrm{M}_{3}}{t_{3}-t_{1}}=\dfrac{\mathrm{M}_{1} \mathrm{M}_{3}}{2 \tau}=\dfrac{72\text{,}5 \times 10^{-2}}{2 \times 50 \times 10^{-3}}= 7\text{,}3 m\cdots-1
2. Choisir une échelle de représentation des vitesses (voir doc. 4). En fonction de l'échelle choisie, tracer le vecteur vitesse \vec{v}_{2} parallèle au segment \mathrm{M}_{1} \mathrm{M}_{3}, partant de \text{M}_{2} et d'une longueur adaptée à l'échelle qui a été choisie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Trajectoires dans la neige


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3Trajectoire rectiligne d'un skieur


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
t_{2} et t_{1} sont des dates tandis que \Delta t est une durée. La durée est définie comme le temps séparant deux dates, par exemple : \Delta t=t_{2}-t_{1}.
La durée séparant deux positions sur une chronophotographie est souvent notée \tau.
La durée séparant deux positions sur une chronophotographie est souvent notée \tau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Vecteur vitesse \vec{v}_{2} au point \text{M}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Variation du vecteur vitesse
Décrire l'évolution du vecteur vitesse d'un système au cours du mouvement consiste à décrire la variation de ses trois caractéristiques : direction, sens et valeur.
Décrire l'évolution du vecteur vitesse d'un système au cours du mouvement consiste à décrire la variation de ses trois caractéristiques : direction, sens et valeur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AVariation de la valeur du vecteur vitesse
Si la valeur du vecteur vitesse augmente, le mouvement est accéléré (doc. 5).
Si la valeur du vecteur vitesse diminue, le mouvement est décéléré (ou ralenti).
Si la valeur du vecteur vitesse est constante, le mouvement est uniforme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Vecteur vitesse d'une fusée


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVariation de la direction du vecteur vitesse
Si la direction du vecteur vitesse est constante lors du mouvement, alors le mouvement est rectiligne (doc. 5).
Lors d'un mouvement circulaire ou curviligne, la direction du vecteur vitesse varie (doc. 6).
Lors d'un mouvement circulaire ou curviligne, la direction du vecteur vitesse varie (doc. 6).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application
On a représenté le vecteur vitesse de la Lune pour quatre positions successives (doc. 7). Décrire la variation du vecteur vitesse de la Lune dans le référentiel géocentrique.
Sur le schéma, on remarque que les quatre segments fléchés ont la même longueur. Donc la valeur de la vitesse de la Lune est constante. \vec{v}_{1} et \vec{v}_{3} tandis que \vec{v}_{2} et \vec{v}_{4} sont verticaux. Ainsi, la direction du vecteur vitesse varie au cours du mouvement.
Donc, lors du mouvement de la Lune dans le référentiel géocentrique, la valeur du vecteur vitesse de la Lune est constante, tandis que sa direction varie.
Corrigé
Sur le schéma, on remarque que les quatre segments fléchés ont la même longueur. Donc la valeur de la vitesse de la Lune est constante. \vec{v}_{1} et \vec{v}_{3} tandis que \vec{v}_{2} et \vec{v}_{4} sont verticaux. Ainsi, la direction du vecteur vitesse varie au cours du mouvement.
Donc, lors du mouvement de la Lune dans le référentiel géocentrique, la valeur du vecteur vitesse de la Lune est constante, tandis que sa direction varie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un mouvement est rectiligne uniforme si le vecteur vitesse est constant tout au long du mouvement.
Un mouvement est rectiligne non uniforme si la direction et le sens sont identiques tout au long du mouvement mais que la valeur de la vitesse varie.
Un mouvement est rectiligne non uniforme si la direction et le sens sont identiques tout au long du mouvement mais que la valeur de la vitesse varie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6Trajectoire elliptique d'un astre

Au cours de son mouvement, son vecteur vitesse varie en direction et en valeur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Vitesse de la Lune

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.


Au cours de sa course, la vitesse du joueur de baseball augmente : son mouvement n'est pas uniforme.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

