Rappels de collège
Proportionnalité et statistiques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Deux grandeurs sont proportionnelles lorsque les valeurs de l'une sont obtenues en multipliant les valeurs de l'autre toujours par un même nombre, appelé le coefficient de proportionnalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le prix payé à la station service est proportionnel au volume d'essence mis dans le réservoir.Le coefficient de proportionnalité est le prix au litre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Pour remplir un tableau de proportionnalité, il existe différentes méthodes.1. Coefficient de proportionnalité pour passer d'une ligne à l'autre.
Exemple

2. Coefficient appliqué à une colonne.
Exemple

3. Méthode par passage à l'unité : on calcule pour 1 kg avant de terminer de remplir pour 6.
Exemple

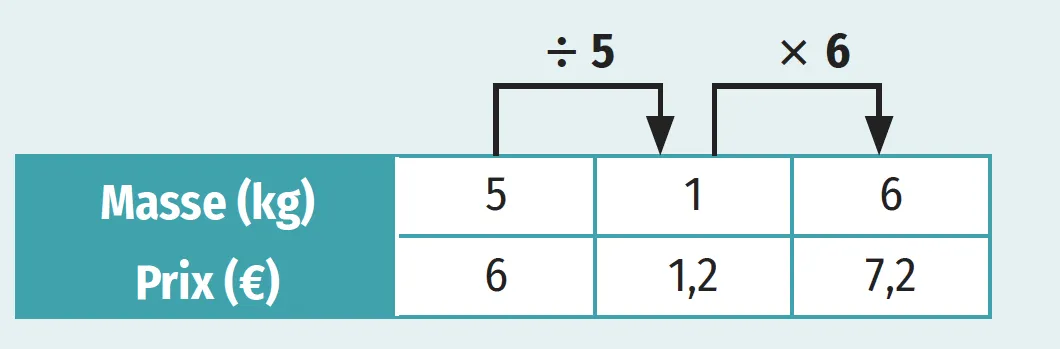
4. Quatrième proportionnelle ou méthode du produit en croix.
Exemple

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Une situation de proportionnalité est modélisée par une fonction linéaire et, dans un repère, représentée par une droite qui passe par l'origine de ce repère.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Chez le primeur, 4 kg de pommes coûtent 2 euros. Cette situation peut être décrite par la fonction linéairef: x \longmapsto \dfrac{1}{2} x
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Calculer a% de b c'est calculer \dfrac{a}{100} \times b ou encore \dfrac{a \times b}{100}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
20% de 30 c'est \dfrac{20 \times 30}{100}=\dfrac{600}{100}=6
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
12
Parmi les couples de grandeurs suivants, lesquels sont proportionnels ?
a. La température d'un réfrigérateur et la distance Terre-Lune.
b. Le poids de tomates dans un sachet et le prix du sachet.
c. La puissance d'une voiture et le nombre de ses vitres.
d. L'âge d'une personne et sa taille.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
13
Le laiton jaune est un alliage métallique de cuivre et de zinc. Un morceau de 650 g de laiton jaune contient 403 g de cuivre. Quel est le pourcentage de cuivre contenu dans ce laiton jaune ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
14
Une voiture roule à vitesse constante de 45 km/h. À l'aide
d'un tableau de proportionnalité, déterminer la distance qu'elle
parcourt en :
10 min ; 25 min ; 35 min ; 0,8 h ; 1,5 h ; 1 h 25.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
15
Sur les 25 kg de fraises récoltées, le primeur en a jeté 12 %. Quelle masse de fraises a-t-il jetée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
16
Résoudre cet exercice sans passer par un tableau de proportionnalité : 6 oeufs coûtent 1,86 euros. Combien coûtent 10 oeufs ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Statistiques descriptives
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
On peut représenter les données d'une série statistique à l'aide d'un tableau simple.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Tableau simple.
| Moyenne de français | Moyenne de maths | Moyenne de SVT | Moyenne de LV1 |
| 13 | 11 | 9 | 14 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Lorsque deux données sont liées, on peut utiliser un tableau à double entrée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Tableau à double entrée.

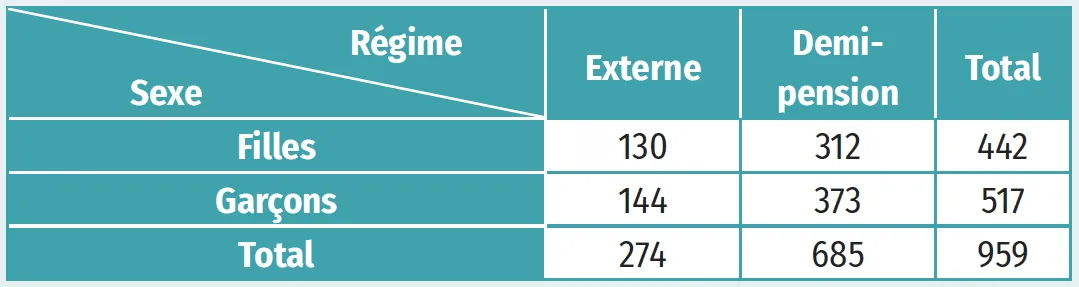
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
On peut représenter une série statistique à l'aide d'un
diagramme en bâton :- en abscisse apparaissent les valeurs ;
- en ordonnées apparaissent les effectifs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Représentation en diagramme en bâtons.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
La moyenne d'une série statistique s'obtient en multipliant tous les effectifs par la valeur du caractère correspondant et en divisant par l'effectif total.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
| Nombre de buts marqués | 0 | 1 | 2 | 3 | 4 | Total |
| Effectifs | 5 | 6 | 4 | 3 | 1 | 19 |
La moyenne des buts marqués est de :
\dfrac{5 \times 0+6 \times 1+4 \times 2+3 \times 3+1 \times 4}{19} \approx 1,4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Dans une série statistique dont les valeurs sont rangées par ordre croissant, on appelle médiane un nombre qui partage cette série en deux groupes de même effectif.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans la série précédente, l'effectif total est 19. La médiane est donc donnée par la 10e valeur : elle vaut 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
Lʼétendue dʼune série statistique est lʼécart entre la plus
grande valeur et la plus petite valeur de la série.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Dans la série précédente, l'étendue vaut 4 - 0, soit 4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
►
La fréquence dʼune valeur est la proportion que représente son effectif par rapport à lʼeffectif total. Cʼest un nombre compris entre 0 et 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
La fréquence de la valeur 1 est de \dfrac{6}{19}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
17
Voici les notes obtenues au dernier devoir.
| Notes | 14 | 12 | 11 | 10 | 9 | 8 | 5 |
| Effectifs | 3 | 9 | 5 | 3 | 3 | 1 | 1 |
Calculer la moyenne, la médiane et l'étendue de cette série. Interpréter les résultats obtenus.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour s'exercer
18
Sur 100 habitants en France, en 2015, 47 sont allés au cinéma 0 fois, 29 y sont allés une fois, 15 y sont allés deux fois, 9 y sont allés trois fois et plus. Représenter ces informations à l'aide du diagramme qui semble le plus adapté.
Cliquez pour accéder à une zone de dessin
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

