	Pour commencer	Différenciation	Pour s'entraîner	Pour aller plus loin
Savoir identifier un domaine spectral à l'aide d'une échelle de fréquences ou de longueurs d'onde :	10 11		21
Connaître et utiliser l'expression donnant l'énergie d'un photon :	13		18
Mettre en œuvre un protocole expérimental permettant d'obtenir un spectre d'émission :				25
Exploiter un diagramme de niveaux d'énergie en utilisant les relations \lambda=\dfrac{c}{\nu} et \Delta E=h \cdot \nu :		14 15 16		27

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour s'échauffer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Donnée

Constante de Planck : h=6\text{,}63 \times 10^{-34} J·s ;
1 eV =1\text{,}60 \times 10^{-19} J ;
Célérité de la lumière dans le vide : c=3\text{,}00 \times 10^{8} m·s^-1.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Relation entre longueur d'onde, célérité et fréquence

Annabelle vient d'installer un routeur Wi-Fi à son domicile. La fréquence d'utilisation est une onde hertzienne de 2,4 GHz.

Calculer la longueur d'onde de l'onde en mètre (m).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Expression de l'énergie d'un photon (1)

Un lecteur Blu-ray utilise un laser de fréquence 7\text{,}41 \times 10^{5} GHz.

Calculer l'énergie (J) et la longueur d'onde (nm) du photon correspondant.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Domaine spectral

Indiquer à quel domaine spectral appartiennent les ondes utilisées par les appareils suivants : routeur Wi‑Fi, scanner de bagages à l'aéroport, phare de voiture et télécommande de télévision.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Expression de l'énergie d'un photon (2)

Calculer l'énergie en joule (J) puis en électron-volt (eV) d'un photon issu d'un pointeur laser de longueur d'onde \lambda=650 nm.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Expression de l'énergie d'un photon

Jean possède un pointeur laser sur lequel est écrit \lambda= 532 nm.

Calculer la fréquence et l'énergie des photons associées exprimées toutes deux dans leur unité officielle respective.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Exploiter un diagramme d'énergie

Préciser l'état dans lequel se trouve l'électron pour chaque niveau d'énergie du doc. 1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Expression de l'énergie d'un photon (3)

Doc. 1 Calculer la variation d'énergie \Delta E entre les niveaux E_{\mathrm{a}} à E_{\mathrm{c}}. Puis, convertir et exprimer sa valeur en joule. Enfin, préciser quels sont les deux phénomènes possibles liés à cette différence d'énergie.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 1
Diagramme des niveaux d'énergie de l'atome de potassium

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

C
Exploiter un diagramme d'énergie

Avec le doc 1, préciser la nature de la transition et la représenter sur le diagramme quand l'électron passe du niveau : (a) Ea à Ed ; (b) du niveau Ec à Eb .

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour commencer

Le modèle ondulatoire

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
La photodiode

✔ APP : Extraire une information utile

Une photodiode est un composant semi-conducteur capable de générer un courant électrique à partir d'un rayonnement électromagnétique.

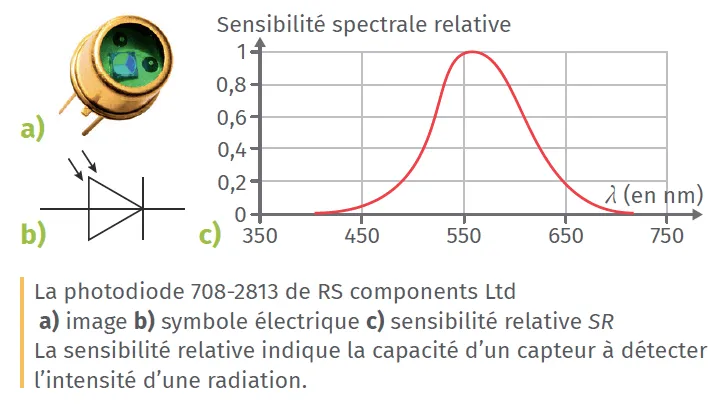
Schéma photodiode : image, symbole électrique et courbe de sensibilité spectrale. Illustration de la détection de l'intensité lumineuse.

1. À l'aide du graphique de la sensibilité relative S_{\mathrm{R}}=\mathrm{f}(\lambda), indiquer pour quelle longueur d'onde la photodiode est la plus efficace. Indiquer le domaine auquel elle appartient.

2. La photodiode peut-elle détecter les radiations infrarouges ? ultraviolettes ? Expliquer.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
Le laser chirurgical au dioxyde de carbone \bf{\mathrm{CO}_{2}}

✔ APP : Formuler un résultat attendu

Le laser au \mathrm{CO}_{2} existe depuis 1964. Sa puissance pouvant atteindre un kilowatt, on l'utilise pour le découpage et les soudures industrielles. Toutefois, il est également utilisé en chirurgie médicale car il opère à une longueur d'onde très bien absorbée par la peau.

Déterminer la longueur d'onde et le domaine auquel il appartient sachant que le laser fonctionne à une fréquence de 28\text{,}3 THz.

Données

Constante de Planck : h=6\text{,}63 \times 10^{-34} J·s ;
1 eV =1\text{,}60 \times 10^{-19} J ;
Célérité de la lumière dans le vide : c=3\text{,}00 \times 10^{8} m·s^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

D
La communication Wi-Fi

✔ APP : Formuler un résultat attendu

Les appareils Wi-Fi communiquent avec deux fréquences hertziennes ou ondes submillimétriques de valeur 2,4 GHz ou 5,0 GHz.

1. À quel domaine ces deux ondes appartiennent-elles ?

2. La vitesse de propagation (dans le vide) dépend-elle de leur fréquence ? Justifier.

3. Calculer les deux longueurs d'ondes \lambda_{inf} et \lambda_{sup} correspondantes aux deux fréquences utilisées.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Le modèle particulaire

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
La thermographie (infrarouge)

✔ RAI/ANA : Associer les unités de mesure à leurs grandeurs correspondantes

Utilisée dans de nombreux domaines, la thermographie permet de visualiser à distance la température d'un objet ou d'une personne. En médecine, l'imageur transforme le rayonnement infrarouge mesuré dans une bande spectrale comprise entre 2 et 5 \mum en un signal électrique pour le coder ensuite en fausse couleur.

Photographie caméra thermique infrarouge analysant une maison. L'écran affiche une image thermique des pertes de chaleur.

Calculer la bande de fréquence et d'énergie du photon détecté.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
La radiothérapie

✔ RAI/ANA : Associer les unités de mesure à leurs grandeurs correspondantes

La radiothérapie est un traitement local contre le cancer. Avec l'aide d'un accélérateur linéaire, on expose une personne à un rayonnement ionisant d'une fréquence voisine de 3 \times 10^{20} Hz pour bloquer la capacité des cellules cancérigènes à se multiplier.

Photographie : patient en radiothérapie, tête immobilisée, lasers ciblant la tumeur.

1. Calculer l'énergie transportée par le photon en MeV.

2. Comparer sa valeur avec celle du visible (2 eV en moyenne) et l'infrarouge (exercice

). Conclure.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

La quantification d'énergie

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

E
Le lithium

✔ Compétence

Bien que très utilisé dans la production d'accumulateurs rechargeables, ce métal alcalin n'existe pas à l'état natif car il s'oxyde très rapidement. C. Gmelin a observé dès 1818 que ses sels donnent une flamme rouge et intense.

1. Donner une explication à l'existence de niveaux d'énergie dans un atome tel que le lithium.

2. Calculer l'écart d'énergie \Delta E correspondant à la transition entre le premier état excité et le fondamental.

3. Après avoir calculé, en joules, l'énergie E_r du photon émis, vérifier si la longueur d'onde \Delta_r est cohérente avec la couleur observée.

Données

Niveaux d'énergie de l'atome de lithium (eV)

E1 = -5{,}39
E2 = -3{,}54
E3 = -2{,}01
E4 = -1{,}55
E5 = -1{,}51

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Une notion, trois exercices
Différenciation

Savoir‑faire : Exploiter un diagramme de niveaux d'énergie en utilisant les relations \lambda=\dfrac{c}{\nu} et \Delta E=h \cdot \nu

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Info

L'hydrogène est l'élément majeur de l'Univers. Tandis que le gaz dihydrogène est très utilisé dans l'industrie du pétrole pour ses propriétés chimiques, on utilise l'atome d'hydrogène en laboratoire afin de régler précisément d'autres appareils à l'aide d'une lampe à décharge.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14

L'atome d'hydrogène : série de Paschen

✔ APP : Extraire une information utile

1. Déterminer la différence d'énergie \Delta E, en eV, associée au passage de l'électron du niveau d'énergie 7 au niveau d'énergie 3.

2. Exprimer cette différence \Delta E en joule.

3. Que devient cette énergie cédée par l'atome ?

4. Déterminer la fréquence, puis la longueur d'onde de la radiation associée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
L'atome d'hydrogène : série de Balmer

✔ APP : Maîtriser le vocabulaire

1. Déterminer la différence d'énergie \Delta E, en joule, associée à la transition d'énergie entre les niveaux 3 et 2.

2. Déterminer la fréquence, puis la longueur d'onde de la radiation émise.

3. À quel domaine appartient la radiation émise ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16

L'atome d'hydrogène : série de Lyman

✔ RAI/ANA : Construire un raisonnement, communiquer sur les étapes

Certaines galaxies émettent une raie dite « Lyman-alpha » de longueur d'onde \lambda=121\text{,}6 nm (doc. 1).

Déterminer la transition responsable de cette émission.

Doc. 1
Diagramme des niveaux d'énergie de l'atome d'hydrogène

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Physique-Chimie 1re Spécialité

Pour s'échauffer - Pour commencer

Savoir-faire - parcours d'apprentissage