Chapitre 13
Activité 2 - Activité d'exploration
Des champs en physique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problématique de l'activité
Les interactions gravitationnelles et électrostatiques sont des interactions à distance.
Comment décrit-on ces interactions dans l'espace ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Selon le physicien Maxwell, « le champ crée une toile à travers tout le ciel ». De quel champ peut-il bien s'agir ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1La naissance de la notion de champ
Au milieu du XVIIIe siècle, Leonhard Euler (1707-1783) étudie le mouvement des fluides. Il attribue une vitesse à chaque point d'un liquide en mouvement. La notion de champ est née : elle correspond à l'attribution en chaque point de l'espace de la valeur unique d'une grandeur physique. Euler a répertorié des vitesses mais on peut aussi bien répertorier des températures, des pressions ou même des forces. Les champs sont dits « scalaires » si la grandeur mesurée est scalaire (valeur numérique + unité), ou « vectoriels » si la grandeur est représentée localement par un vecteur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2 Les champs gravitationnel et électrostatique
Une particule chargée \text{A} agit dans l'espace qui l'entoure sur toute particule \text{B} chargée qui s'y trouve. Il en est de même pour une masse \text{A} sur toute la masse présente \text{B} autour d'elle. Ces actions sont modélisées par des forces, desquelles on peut déduire les vecteurs champ \overrightarrow{\mathcal{G}} et \overrightarrow{E} :

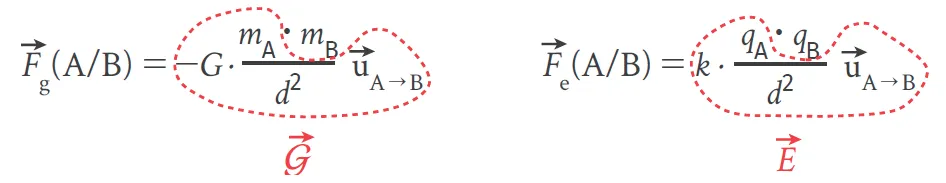

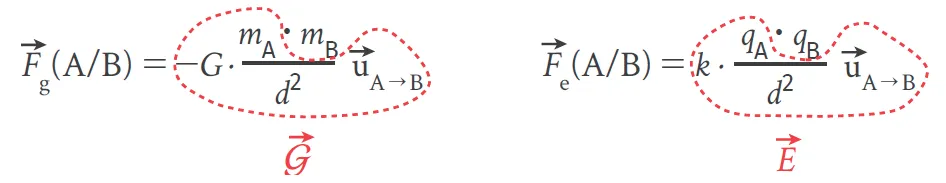
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 3 Cartographier un champ gravitationnel

Afin de cartographier un champ gravitationnel créé par une masse M, on déplace une masse d'essai m_{\mathrm{e}}= 1 kg dans la zone spatiale qui nous intéresse. La force gravitationnelle agissant sur m_{\mathrm{e}} est proportionnelle au champ gravitationnel au niveau de la position de m_{\mathrm{e}}.
Dans cette activité, on déplace la masse d'essai le long de cercles de rayons 1, 2 et 3 mètres. Chaque point représente une position de m_{\mathrm{e}}, occupée tous les 45°.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4 Lignes de champs

Lignes de champ du champ magnétique terrestre.
Les lignes de champs sont des courbes permettant de représenter les champs vectoriels. Elles sont en tout point tangentes aux vecteurs du champ et orientées dans le même sens que celui-ci.
Plus le champ est intense, plus les lignes seront proches les unes des autres.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- k = 8,99 \times 109 N·m2·C-2 ;
- G = 6,67 \times 10-11 N·m2·kg-2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions
Compétence
MATH : Vecteur
1. Doc. 3 Reproduire la carte des positions de la masse d'essai à l'échelle 3 carreaux pour 1 m. Vous pouvez également répondre aux questions de cette activité sur papier.
2. Doc. 2 et 3 On place sur le point central une masse M = 4,0 kg. Après avoir calculé leurs valeurs, représenter les forces d'interaction gravitationnelle de M sur la masse d'essai m_{\mathrm{e}} pour chacune des positions représentées. (Échelle : 1 carreau \rightarrow 1 \times 10-10 N.)
3. Doc. 2 Identifier le lien entre les forces d'interaction gravitationnelle exercées par M sur m_{\mathrm{e}} et le champ gravitationnel créé par M.
4. Doc. 3 et 4 Tracer les lignes de champ du champ représenté. Commenter le dessin.
3. Doc. 2 Identifier le lien entre les forces d'interaction gravitationnelle exercées par M sur m_{\mathrm{e}} et le champ gravitationnel créé par M.
4. Doc. 3 et 4 Tracer les lignes de champ du champ représenté. Commenter le dessin.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Synthèse de l'activité
Que représentent les champs gravitationnel et électrostatique ?
L'image de Maxwell est-elle confirmée par la représentation de champ dans l'activité ?
L'image de Maxwell est-elle confirmée par la représentation de champ dans l'activité ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

