Physique-Chimie 2de
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
1. Constitution et transformations de la matière
Ch. 1
Identification des espèces chimiques
Ch. 2
Composition des solutions aqueuses
Ch. 3
Dénombrer les entités
Ch. 4
Le noyau de l’atome
Ch. 5
Le cortège électronique
Ch. 6
Stabilité des entités chimiques
Ch. 7
Modélisation des transformations physiques
Ch. 8
Modélisation des transformations chimiques
Ch. 9
Synthèse de molécules naturelles
Ch. 10
Modélisation des transformations nucléaires
2. Mouvement et interactions
Ch. 11
Décrire un mouvement
Ch. 12
Modéliser une action sur un système
Ch. 13
Principe d’inertie
3. Ondes et signaux
Ch. 14
Émission et perception d’un son
Ch. 15
Analyse spectrale des ondes lumineuses
Ch. 16
Propagation des ondes lumineuses
Ch. 17
Signaux et capteurs
Méthode
Fiches méthode
Fiches méthode compétences
Annexes
Fiche méthode R
Compétences
Exclusivité numérique
Mathématiques : Pratiquer le calcul numérique
pour télécharger la fiche méthode au format pdfRessource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Chiffres significatifs
❯ Définition
Ce sont les chiffres de la valeur expérimentale qui indiquent la précision de la mesure.
Exemple : une longueur de 2 m est une longueur comprise entre 1\text{,}5 et 2\text{,}5 m. Une longueur de 2\text{,}0 m est comprise entre 1\text{,}95 et 2\text{,}05 m. En sciences physiques, un 0 de plus à droite change beaucoup de choses alors qu'en mathématiques, écrire 2 et 2\text{,}0 reviendrait au même. En sciences, dans 2\text{,}0 m, on dit que le 2 et le 0 sont significatifs.
Ce sont les chiffres de la valeur expérimentale qui indiquent la précision de la mesure.
Exemple : une longueur de 2 m est une longueur comprise entre 1\text{,}5 et 2\text{,}5 m. Une longueur de 2\text{,}0 m est comprise entre 1\text{,}95 et 2\text{,}05 m. En sciences physiques, un 0 de plus à droite change beaucoup de choses alors qu'en mathématiques, écrire 2 et 2\text{,}0 reviendrait au même. En sciences, dans 2\text{,}0 m, on dit que le 2 et le 0 sont significatifs.
❯ Compter les chiffres significatifs d'une valeur
- Un 0 est compté s'il y a au moins un chiffre différent de 0 sur l'une des positions à gauche dans l'écriture du nombre.
- Une puissance de 10 ne compte pas.
Notation
CS : chiffres significatifs.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Expression du résultat d'un calcul
❯ Addition et soustraction
Le résultat a le même niveau de précision que le nombre qui a la décimale la moins précise.
Exemple : d_{1}=2\text{,}0 m, d_{2}=16 cm et D=d_{1}+d_{2}. Avec d_{1}=2\text{,}0 m et d_{2}=0\text{,}16 m. Alors : D=d_{1}+d_{2}=(2\text{,}0 + 0\text{,}16) m =2\text{,}2 m.
d_{1} est précis au 10e de mètre alors que d_{2} l'est au 100e de mètre. Le résultat est donc au 10e de mètre.
Le résultat a le même niveau de précision que le nombre qui a la décimale la moins précise.
Exemple : d_{1}=2\text{,}0 m, d_{2}=16 cm et D=d_{1}+d_{2}. Avec d_{1}=2\text{,}0 m et d_{2}=0\text{,}16 m. Alors : D=d_{1}+d_{2}=(2\text{,}0 + 0\text{,}16) m =2\text{,}2 m.
d_{1} est précis au 10e de mètre alors que d_{2} l'est au 100e de mètre. Le résultat est donc au 10e de mètre.
❯ Multiplication et division
Le résultat a le même nombre de chiffres significatifs que le terme le moins précis.
Exemple : v=\dfrac{2 \pi R}{t}=\dfrac{2 \pi \times 5\text{,}42}{1\text{,}5 \times 10^{2}}=2\text{,}3 \times 10^{-1} m·s‑1
2 \pi et 102 ne sont pas issues de mesures : ces valeurs sont exactes. Il n'y a donc pas de CS à compter.
5\text{,}42 a 3 CS et 1\text{,}5 a 2 CS \rightarrow 2 CS au résultat.
Le résultat a le même nombre de chiffres significatifs que le terme le moins précis.
Exemple : v=\dfrac{2 \pi R}{t}=\dfrac{2 \pi \times 5\text{,}42}{1\text{,}5 \times 10^{2}}=2\text{,}3 \times 10^{-1} m·s‑1
2 \pi et 102 ne sont pas issues de mesures : ces valeurs sont exactes. Il n'y a donc pas de CS à compter.
5\text{,}42 a 3 CS et 1\text{,}5 a 2 CS \rightarrow 2 CS au résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Estimer la réussite d'une mesure
❯ Remarque : X_{\text {théo}} peut aussi être accompagné d'une incertitude. Elle est donnée si besoin.
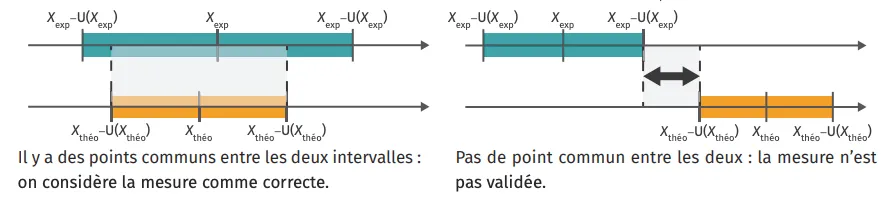
- Regarder si l'intervalle de confiance de X_{\text {théo}} a des points communs avec celui de X_{\text {exp}}.
- Estimer si l'écart relatif (noté \text{E}(X)) est inférieur à 5 % (critère arbitraire classique au lycée).
E(X)=\left|\dfrac{X_{\text {théo}}-X_{\text {exp}}}{X_{\text {théo}}}\right| Il indique si l'écart entre X_{\text {exp}} et X_{\text {théo}} est important ou non. Il permet donc d'estimer la qualité du résultat : plus il est petit, et meilleure est la mesure.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une id ée !
Oups, une coquille
