Nos classiques
Sommaire
Mes pages
N° Page
Réviser avec Genially
Genially
/ 157
Page précédente
Chapitre 7

Exercices de consolidation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Périmètre et aire

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7

Soit un carré de 11 cm de côté.

1. Calculer le périmètre de ce carré.
2. Calculer l'aire de ce carré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
# Copie d'élève

Un professeur de mathématiques donne l'exercice suivant. Voici la copie de Romane.

Soit un rectangle de longueur 18 m et de largeur 6,5 m.

a) Le périmètre de ce rectangle est :
P=18+6,5=24,5 \mathrm{~cm}.

b) L'aire de ce rectangle est :
A=18 \times 6,5=117 \mathrm{~cm}.

1. Vérifier les réponses de Romane.
2. Proposer une correction détaillée de cet exercice.
3. Rédiger un commentaire à Romane en lui expliquant où se situe(nt) son (ou ses) erreur(s).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9

Soit un disque de diamètre 8 cm.

1. Donner le rayon de ce disque.
2. Calculer le périmètre de ce disque, arrondi au dixième.
3. Calculer l'aire de ce disque, arrondie au dixième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10

Associer chaque nature de triangle à sa définition.
Un triangle isocèle

Un triangle équilatéral

Un triangle rectangle
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11

Soit la configuration ci-dessous.

Triangle ABC

1. Donner la nature du triangle \mathrm{ABC}.
2. Calculer le périmètre du triangle \mathrm{ABC}.
3. Calculer l'aire du triangle \mathrm{ABC}.
4. Calculer l'angle \widehat{\mathrm{CAB}}. On rappelle que la somme des angles d'un triangle vaut 180°.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Solides usuels et volume

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12

Donner le nom du solide usuel modélisant chacun de ces desserts en chocolat.

1.
Placeholder pour Dessert chocolat sphérique glacé, décoré de brisures et copeaux blancs, présenté sur fond blanc avec fourchette dorée.Dessert chocolat sphérique glacé, décoré de brisures et copeaux blancs, présenté sur fond blanc avec fourchette dorée.
2.
Placeholder pour Photo de pyramides en chocolat disposées sur fond rougePhoto de pyramides en chocolat disposées sur fond rouge
3.
Placeholder pour Photo de deux entremets chocolat glacés, décor noisettesPhoto de deux entremets chocolat glacés, décor noisettes
4.
Placeholder pour Trois chocolats cubes, bruns et brillants, posés sur fond beige.Trois chocolats cubes, bruns et brillants, posés sur fond beige.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13

Pour chacune des situations suivantes, choisir la bonne réponse.

1. Le volume d'un cube de 7 cm de côté est de :




2. Le volume d'un pavé droit de longueur 9 m, de largeur 2 m et de hauteur 4 m est de :




3. Le volume d'un cylindre de hauteur 30 cm et de rayon 5 cm est d'environ :


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14

Calculer le volume, arrondi à l'unité, de chacun des solides suivants.

1. Une pyramide de base carrée de côté 80 m et de hauteur 50 m.
2. Une boule de rayon 8 cm.
3. Un cylindre droit de hauteur 2 m et de rayon 1,5 m.
4. Un cône de base de diamètre 28 cm et de hauteur 90 cm.
Formules
Volume de la pyramide : \mathcal{V}=\frac{1}{3} \times \mathcal{A}_{\text {base }} \times h.
Volume du cône : \mathcal{V}=\frac{1}{3} \times \mathcal{A}_{\text {base }} \times h.
Volume de la boule : \mathcal{V}=\frac{4}{3} \times \pi \times \mathrm{R}^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Agrandissement et réduction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15

Soit un pavé droit de longueur 12 cm, de largeur 8 cm et de hauteur 3 cm.

1. Calculer le volume de ce pavé droit.
 On agrandit ce pavé droit par un rapport k = 2. 2. Déterminer les dimensions de ce nouveau pavé droit.
3. Calculer le volume de ce nouveau pavé droit.
4. Vérifier que, lors de l'agrandissement, le volume du pavé a été multiplié par k^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16

Soit un carré de 20 cm de côté.

1. Calculer l'aire de ce carré.
 On souhaite représenter ce carré à l'échelle 1/8. 2. Calculer l'aire de ce nouveau carré.
3. Déterminer par combien a été multipliée l'aire du carré lors de la réduction.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Théorème de Pythagore et sa réciproque

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
#Copie d'élève

On considère la figure suivante.

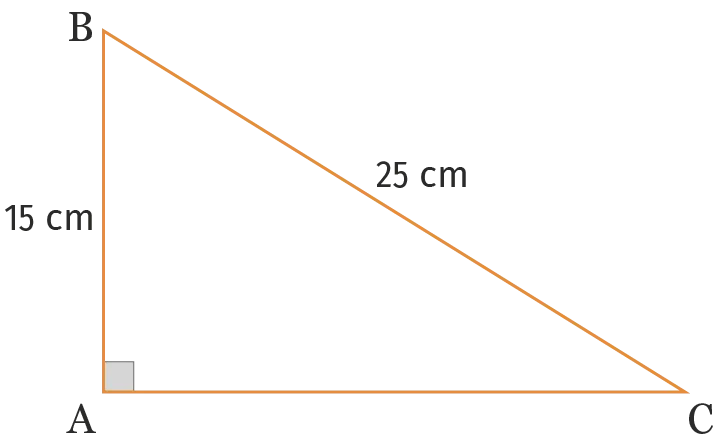
Placeholder pour Diagramme : triangle rectangle avec hypoténuse de 25 cm et un côté de 15 cm.Diagramme : triangle rectangle avec hypoténuse de 25 cm et un côté de 15 cm.

Lors d'un contrôle, Titouan devait calculer la longueur \mathrm{AC} et voici sa copie.

Dans le triangle ABC rectangle en A, le théorème de Pythagore s'écrit : AC^2 = AB^2 + BC^2.
On obtient : A C^2=15^2+25^2=850.
Ce qui donne : A C=\sqrt{850} \approx 29,2 \mathrm{~cm}.
1. Vérifier les calculs de Titouan.
2. Proposer une correction détaillée de cet exercice.
3. Rédiger le commentaire que le professeur pourrait faire à Titouan afin de lui expliquer son erreur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18

Soit un triangle \mathrm{FGH} rectangle en \mathrm{F} avec \mathrm{FG = 1 cm} et \mathrm{FH = 7 cm}.

1. Représenter cette figure à main levée.
Cliquer ici pour avoir accès à un espace de dessin
2. Calculer la longueur \mathrm{GH}, arrondie au centième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19

Soit un triangle \mathrm{PLM} rectangle en \mathrm{P} avec \mathrm{PL = 21 cm} et \mathrm{LM = 27 cm}.

1. Représenter cette figure à main levée.
Cliquer ici pour avoir accès à un espace de dessin
2. Calculer la longueur \mathrm{PM}, arrondie au centième.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20

Dans chacune des configurations suivantes, déterminer si le triangle est rectangle. Si oui, préciser en quel point.

1. \mathrm{BC = 75 m} ; \mathrm{BR = 45 m} ; \mathrm{CR = 60 m}.
2. \mathrm{TS = 21 cm} ; \mathrm{SZ = 26 cm} ; \mathrm{ZT = 35 cm}.
3. \mathrm{GH = 52 m} ; \mathrm{HK = 55 m} ; \mathrm{KG = 19 m}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Théorème de Thalès

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21

On considère la figure suivante et on donne \mathrm{(BC)//(EF)}.

Triangles

1. Calculer la longueur \mathrm{EF}.
2. Calculer la longueur \mathrm{AF}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22

Soit les points \mathrm{K}, \mathrm{L} et \mathrm{S} alignés d'une part et les points \mathrm{K}, \mathrm{M} et \mathrm{T} alignés d'autre part.
On sait que \mathrm{(LM)} et \mathrm{(ST)} sont parallèles et que \mathrm{KL = 4 cm}, \mathrm{KS = 6 cm} et \mathrm{ST = 13,5 cm}.

1. Représenter cette figure à main levée.
Cliquer ici pour avoir accès à un espace de dessin
2. Calculer la longueur \mathrm{LM}.
Page suivante

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.