Livret maths 7
Graphes orientés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Point de cours 1Graphes orientés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définitions
- On appelle graphe un ensemble S de sommets reliés par un ensemble V d'arcs (ou d'arêtes).
- Deux sommets reliés par un arc sont dits adjacents.
- Le graphe peut être ponderé et/ou oriente.
- Un graphe orienté est un graphe dont les arêtes sont associées à une direction.
- Un graphe pondéré est un graphe dont les arêtes sont associées à une valeur.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Le graphe ci-dessous (orienté et pondéré) peut représenter les échanges de populations entre deux villes A et B : chaque année, 40 % des habitants passent de la ville A à la ville B et 20 % de ceux de la ville B partent dans la ville A. Les autres restent dans leur ville d'origine.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Remarques
- Le réseau Internet est un graphe composé de l'ensemble des sites Web connectés entre eux par des liens URL.
- On gère la circulation dans une ville à l'aide de graphe dont les sommets sont les feux tricolores et les arcs sont les rues.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Calcul de coût de parcours.suivants.
Le graphe ci-contre indique le prix du péage entre plusieurs villes.
Quel est le parcours le moins coûteux pour aller de la ville D à la ville A ?

Quel est le parcours le moins coûteux pour aller de la ville D à la ville A ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
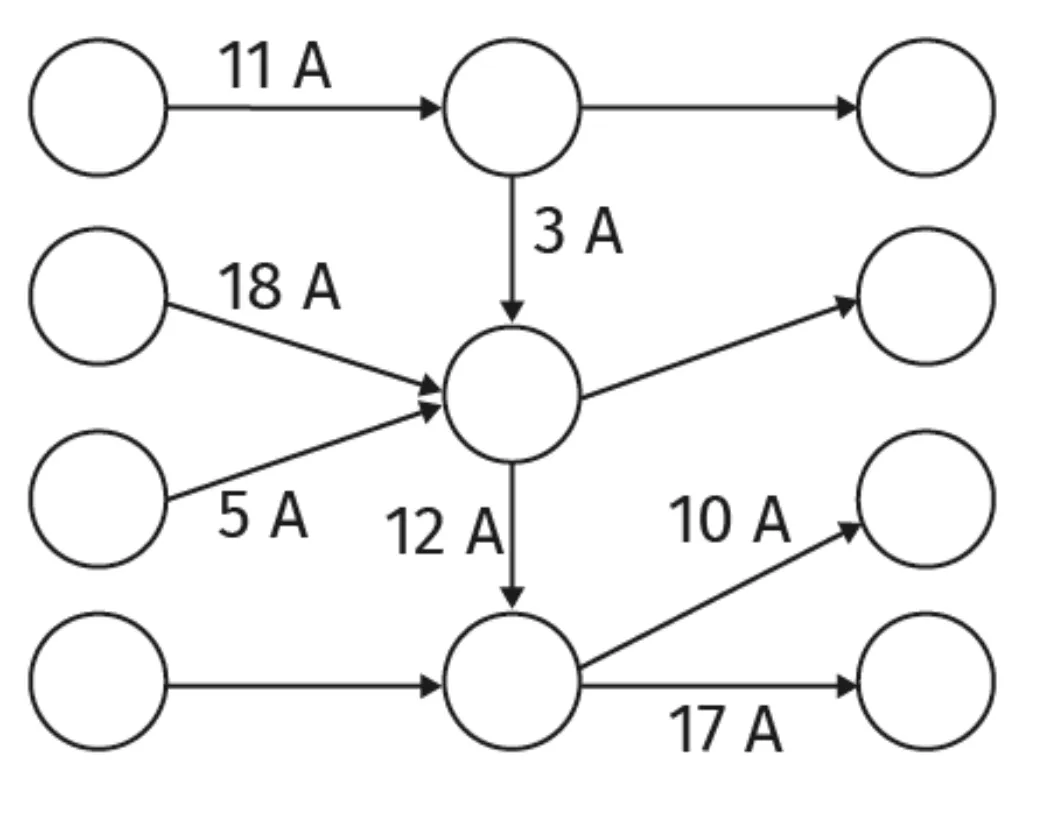
2 Réseau électrique.
Le graphe ci-contre représente un réseau électrique dont l'intensité du courant (en ampère) est
indiquée sur chaque arc. Les intensités arrivant à un sommet intermédiaire sont égales aux intensités en sortant.
 a. Déterminer l'intensité circulant dans la branche ED.
a. Déterminer l'intensité circulant dans la branche ED.
b. L'intensité dans la branche EC passe à 26 A. Proposer de nouvelles valeurs pour les branches AE et BE.

b. L'intensité dans la branche EC passe à 26 A. Proposer de nouvelles valeurs pour les branches AE et BE.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Optimisation du temps de parcours.
Le graphe ci-contre indique les temps de parcours entre plusieurs villes.


a. Ce graphe est-il eulérien ?
b. Quel trajet permet de joindre les villes A et F en un temps minimal ?
b. Quel trajet permet de joindre les villes A et F en un temps minimal ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Échange de populations.Échange de populations.
Deux villes A et B s'échangent des populations selon la modélisation ci-dessous. La première année, la ville A compte 150 000 habitants et la ville B en compte 80 000.
 a. Combien d'habitants vivront dans chaque ville au bout d'un an ? De deux ans ? De trois ans ?
a. Combien d'habitants vivront dans chaque ville au bout d'un an ? De deux ans ? De trois ans ?
b. Quelle évolution peut-on prévoir sur le long terme ?

b. Quelle évolution peut-on prévoir sur le long terme ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AUn réseau simple.
Un poste de distribution est alimenté par 3 centrales et distribue le courant à 3 villes. L'intensité des courants arrivant au poste sont : I_1 = 400 A, I_2 = 240 A et I_3 = 330 A. L'intensité des courant en sortant sont : I_4 = 250 A, I_5 = 300 A et I_6 = 150 A.
Les lois physiques impliquent que la somme des courants arrivant à un nœud (poste de distribution) est égale à la somme des courants en sortant.
a. Réaliser le graphe orienté représentant cette situation.
b. Le graphe réalisé respecte-t-il les contraintes de l'énoncé ? Si non, le compléter avec le(s) sommet(s) et arc(s) nécessaires. Indiquer ce à quoi peuvent correspondre ces ajouts dans la réalité.
Les lois physiques impliquent que la somme des courants arrivant à un nœud (poste de distribution) est égale à la somme des courants en sortant.
a. Réaliser le graphe orienté représentant cette situation.
Cliquez pour accéder à une zone de dessin
b. Le graphe réalisé respecte-t-il les contraintes de l'énoncé ? Si non, le compléter avec le(s) sommet(s) et arc(s) nécessaires. Indiquer ce à quoi peuvent correspondre ces ajouts dans la réalité.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BUn réseau plus complet.
Les lois physiques impliquent que la somme des courants arrivant à un nœud (poste de distribution) est égale à la somme des courants en sortant.
Compléter le graphe orienté ci-dessous représentant un réseau électrique.

Compléter le graphe orienté ci-dessous représentant un réseau électrique.


1
2
3
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

