Chapitre 5
Exercices
Objectif Bac
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Comprendre les attendusÖtzi
✔ APP : Extraire l'information utile
✔ APP : Faire des prévisions à l'aide d'un modèle
✔ APP : Faire des prévisions à l'aide d'un modèle


Ötzi est une momie retrouvée le 19 septembre 1991, piégée dans la glace à plus de 3 000 m d'altitude
en Italie. Son état intact, grâce au gel, en fait une découverte remarquable.
Une fois mort, la quantité initiale de carbone 14 (90 ng) contenue dans le corps humain décroît. Les scientifiques ont donc utilisé cette méthode pour estimer l'âge d'Ötzi. Ils ont découvert que cette momie possédait une activité radioactive en carbone 14 de 7,91 kBq.
1. Calculer le nombre de noyaux de carbone 14 à la mort d'Ötzi.
2. Déterminer le temps de demi-vie du carbone 14.
Une fois mort, la quantité initiale de carbone 14 (90 ng) contenue dans le corps humain décroît. Les scientifiques ont donc utilisé cette méthode pour estimer l'âge d'Ötzi. Ils ont découvert que cette momie possédait une activité radioactive en carbone 14 de 7,91 kBq.
1. Calculer le nombre de noyaux de carbone 14 à la mort d'Ötzi.
2. Déterminer le temps de demi-vie du carbone 14.
3. Déterminer le nombre de noyaux de carbone 14 toujours présents dans la momie.
4. En déduire l'âge d'Ötzi. Préciser les limites de ce type de datation.
4. En déduire l'âge d'Ötzi. Préciser les limites de ce type de datation.
Doc.
Évolution du nombre de noyaux au cours du temps

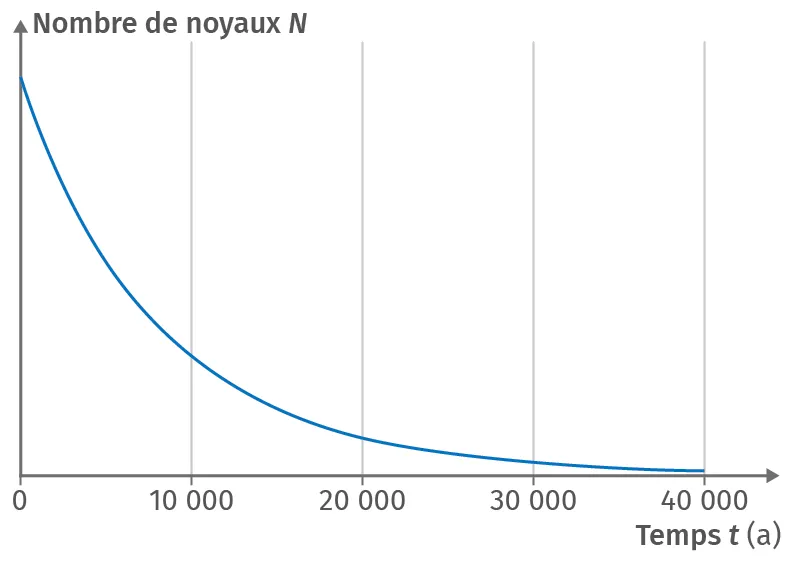
Détails du barème
TOTAL /5 pts
1 pt
1.
Calculer le nombre de noyaux avec les données 0,5 pt
2. Savoir lire un graphique
1 pt
3. Déterminer un nombre de noyaux à partir d'une activité radioactive
1,5 pt
4. Appliquer une relation mathématique 1 pt
4. Faire preuve d'exprit critique
➜ Retrouvez plus d'exercices dans le Livret Bac
Données
- Masse molaire du carbone 14 : M(^{14}\text{C}) = 14{,}0 g·mol-1
- Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23} mol-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Hypertension et volume sanguin
✔ REA/MATH : Utiliser des outils mathématiques
✔ RAI/MOB : Modéliser une transformation
✔ RAI/MOB : Modéliser une transformation

Suite à un examen médical, un patient apprend qu'il souffre d'hypertension. Le médecin suspecte
que ce trouble est dû à un volume sanguin trop important (supérieur à 7 L). Il décide donc de lui prescrire des examens complémentaires. On lui injecte dans le sang 10 mL d'une solution contenant initialement du sodium 24 à une concentration de 1{,}0 \times 10^{-3} mol·L‑1.
1. Donner la composition du noyau de sodium 24. ➜
1. Donner la composition du noyau de sodium 24. ➜
2. Écrire son équation de désintégration \beta ^-.
3. Déterminer la quantité de matière de sodium 24 introduite et en déduire le nombre de noyaux.
Soit N(t) le nombre de noyaux radioactifs présents, à la date t, dans un échantillon.
4. Écrire l'expression de la loi de décroissance N = f(t) en fonction de N_0, le nombre de noyaux initialement présents dans l'échantillon, et t_{1/2}, temps de demi-vie, dont on précisera la définition.
5. Calculer le nombre de noyaux au bout de 7,0 h sachant que le temps de demi-vie du sodium 24 est égal à t_{1/2} = 15{,}0 h.
Au bout de 7,0 h, on peut considérer que le sodium 24 injecté s'est réparti uniformément dans tout le système sanguin. On prélève 10 mL de sang au patient et l'analyse de cet échantillon permet de déterminer une quantité de matière n = 1{,}4 \times 10^{-8} mol de sodium 24.
6. En déduire le volume sanguin du patient. Conclure.
3. Déterminer la quantité de matière de sodium 24 introduite et en déduire le nombre de noyaux.
Soit N(t) le nombre de noyaux radioactifs présents, à la date t, dans un échantillon.
4. Écrire l'expression de la loi de décroissance N = f(t) en fonction de N_0, le nombre de noyaux initialement présents dans l'échantillon, et t_{1/2}, temps de demi-vie, dont on précisera la définition.
5. Calculer le nombre de noyaux au bout de 7,0 h sachant que le temps de demi-vie du sodium 24 est égal à t_{1/2} = 15{,}0 h.
Au bout de 7,0 h, on peut considérer que le sodium 24 injecté s'est réparti uniformément dans tout le système sanguin. On prélève 10 mL de sang au patient et l'analyse de cet échantillon permet de déterminer une quantité de matière n = 1{,}4 \times 10^{-8} mol de sodium 24.
6. En déduire le volume sanguin du patient. Conclure.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Datation d'une carotte glaciaire
✔ RAI/ANA : Utiliser et interpréter des documents
✔ REA/MATH : Résoudre une équation différentielle
✔ REA/MATH : Résoudre une équation différentielle
D'après le sujet Bac S, Réunion, 2009.
Une carotte de glace est formée de couches de neige compressées. Plus on creuse en profondeur, plus on obtient des mesures anciennes sur les composés et éléments chimiques présents à cette époque.


Dans les eaux de surface, le chlore 36 est constamment renouvelé et sa teneur reste constante au cours du temps. Dans la glace, ce renouvellement n'existe plus et la quantité de chlore 36 diminue au cours du temps.
Doc.
Carotte glaciaire


1. Donner la composition du noyau de chlore 36.
2. Préciser en quoi le renouvellement en chlore 36 dans les eaux de surface est important pour la datation.
3. Donner l'équation de la désintégration du chlore 36 sachant qu'un noyau d'argon se forme.
2. Préciser en quoi le renouvellement en chlore 36 dans les eaux de surface est important pour la datation.
3. Donner l'équation de la désintégration du chlore 36 sachant qu'un noyau d'argon se forme.
4. Donner le nom de la particule émise et le type de
radioactivité mise en jeu.
La variation temporelle du nombre de noyaux radioactifs \dfrac{\text{d}N}{\text{d}t} est proportionnelle à la population :
5. Résoudre l'équation différentielle.
6. Donner la définition du temps de demi-vie t_{1/2} et calculer la valeur de la constante radioactive \lambda.
On cherche à déterminer l'âge t_1 d'un échantillon de glace prélevé dans une carotte glaciaire de l'Arctique et pour lequel il n'y a plus que 75 % de noyaux de chlore 36 par rapport à un échantillon récent de même masse.
7. Donner la valeur du rapport \dfrac{N(t_1)}{N_0} pour le morceau de glace étudié.
8. Exprimer, puis calculer l'âge t_1 de l'échantillon.
9. La glace contient également des bulles de dioxyde de carbone \text{CO}_2(\text{g}). Expliquer pourquoi la datation au carbone 14 est inadéquate.
Temps de demi-vie :
La variation temporelle du nombre de noyaux radioactifs \dfrac{\text{d}N}{\text{d}t} est proportionnelle à la population :
-\dfrac{\text{d}N}{\text{d}t} = \lambda \cdot N
5. Résoudre l'équation différentielle.
6. Donner la définition du temps de demi-vie t_{1/2} et calculer la valeur de la constante radioactive \lambda.
On cherche à déterminer l'âge t_1 d'un échantillon de glace prélevé dans une carotte glaciaire de l'Arctique et pour lequel il n'y a plus que 75 % de noyaux de chlore 36 par rapport à un échantillon récent de même masse.
7. Donner la valeur du rapport \dfrac{N(t_1)}{N_0} pour le morceau de glace étudié.
8. Exprimer, puis calculer l'âge t_1 de l'échantillon.
9. La glace contient également des bulles de dioxyde de carbone \text{CO}_2(\text{g}). Expliquer pourquoi la datation au carbone 14 est inadéquate.
Données
Temps de demi-vie :
- t_{1/2}(^{36}\text{Cl}) = 3{,}01 \times 10^5 a
- t_{1/2}(^{14}\text{C}) = 5{,}73 \times 10^3 a
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Traitement thyroïdien
✔ REA/MATH : Utiliser des outils mathématiques
✔ RAI/MOB : Modéliser une transformation
✔ RAI/MOB : Modéliser une transformation
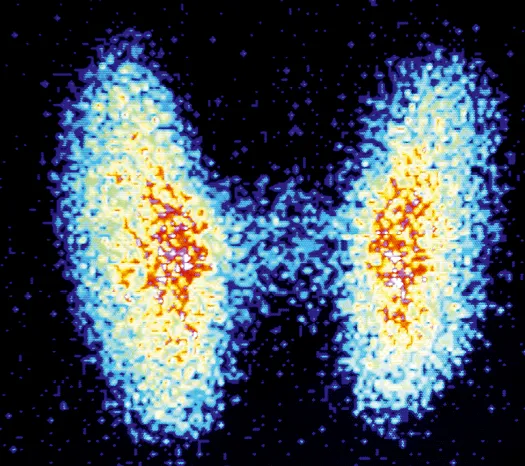
L'hyperthyroïdie est une maladie fréquente qui touche la glande de la thyroïde située dans le cou.
Cette glande produit des hormones qui permettent de réguler la température corporelle, la masse ou encore le rythme cardiaque.
La scintigraphie est une technique de radiographie qui permet d'obtenir une image grâce aux rayons \gamma émis par un traceur radioactif injecté dans le patient tel que le carbone 11. Le carbone 11 subit une désintégration \beta ^+.
La scintigraphie est une technique de radiographie qui permet d'obtenir une image grâce aux rayons \gamma émis par un traceur radioactif injecté dans le patient tel que le carbone 11. Le carbone 11 subit une désintégration \beta ^+.

1. Écrire l'équation de désintégration du carbone 11.
On injecte 2,5 μg de traceur ^{11}\text{C} dans le patient.
2. Déterminer le nombre de noyaux injectés.
3. Donner la loi de décroissance radioactive.
4. À partir de cette loi, vérifier que : \ln(N) = \ln(N_0) - \lambda\cdot t
Un contrôle de cette source au cours du temps donne les résultats suivants :
| N(\times 10^{16}) | 13,7 | 11,5 | 9,74 | 8,21 | 6,93 | 5,85 | 4,93 | 4,16 |
| t(\text{s}) | 0 | 300 | 600 | 900 | 1 200 | 1 500 | 1 800 | 2 100 |
5. Ajouter une ligne au tableau en insérant la valeur de \ln(N) et tracer la courbe \ln(N)en fonction du temps t et déterminer la constante radioactive \lambda.
6. Déterminer le nombre de noyaux radioactifs restants, 24 h après la scintigraphie.
7. En déduire le pourcentage de noyaux désintégrés 24 h après l'examen.
8. Proposer une explication au fait que cet examen peut présenter un danger pour la santé.
Données
- Masse molaire du carbone 11 : M(^{11}\text{C}) = 11{,}0 g·mol-1
- Relations utiles : \ln(a \cdot b) = \ln(a) + \ln(b) et a = \ln(\exp(a))
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

