Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 5
Exercices
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Consommation radioactive en QCM
✔ RAI/ANA : Construire un raisonnement
Le 1er, le 6, le 11 et le 16 septembre 2020, Maria boit, au réveil, un volume d'eau contenant une même quantité de noyaux radioactifs dont l'activité est égale à 40 Bq. Ces noyaux se fixent dans son organisme avant de se désintégrer. La courbe ci-dessous montre la désintégration d'une quantité correspondant à 40 Bq.
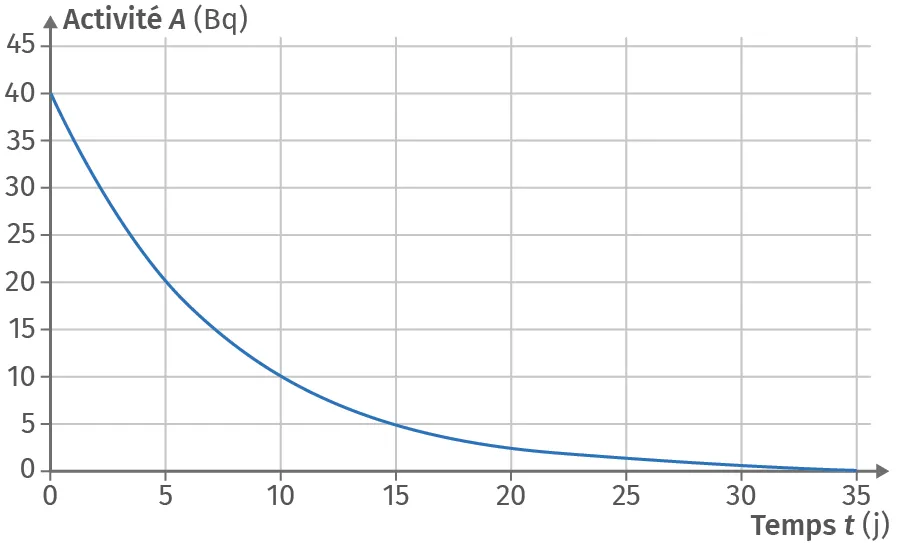
1. Déterminer le nombre de noyaux radioactifs
contenus initialement dans le volume d'eau.
a. N_0 = 2{,}5 \times 10^7.
b. N_0 = 2{,}9 \times 10^7.
c. N_0 = 1{,}7 \times 10^7.
2. Le mercredi 16 septembre 2020, déterminer l'activité de l'organisme de Maria.
a. A = 5 Bq.
b. A = 40 Bq.
c. A = 75 Bq.
3. Préciser à quelle date la moitié de l'activité trouvée précédemment sera atteinte.
a. Le 1er octobre 2020.
b. Le 21 septembre 2020.
c. Le 26 septembre 2020.
a. N_0 = 2{,}5 \times 10^7.
b. N_0 = 2{,}9 \times 10^7.
c. N_0 = 1{,}7 \times 10^7.
2. Le mercredi 16 septembre 2020, déterminer l'activité de l'organisme de Maria.
a. A = 5 Bq.
b. A = 40 Bq.
c. A = 75 Bq.
3. Préciser à quelle date la moitié de l'activité trouvée précédemment sera atteinte.
a. Le 1er octobre 2020.
b. Le 21 septembre 2020.
c. Le 26 septembre 2020.
4. Déterminer l'isotope consommé.
a. Du bismuth 210 de constante radioactive \lambda = 1{,}6 \times 10^{-6} s-1.
b. Du magnésium 28 de constante radioactive \lambda = 9{,}2 \times 10^{-6} s-1.
c. Du silicium 36 de constante radioactive \lambda = 1{,}5 \times 10^5 s-1.
a. Du bismuth 210 de constante radioactive \lambda = 1{,}6 \times 10^{-6} s-1.
b. Du magnésium 28 de constante radioactive \lambda = 9{,}2 \times 10^{-6} s-1.
c. Du silicium 36 de constante radioactive \lambda = 1{,}5 \times 10^5 s-1.
Doc.
Tomographie cérébrale
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Radiographie à l'azote
✔ VAL : Modéliser un ensemble de mesures
Une tomographie par émission de positons est effectuée sur un patient. Pour cela, on injecte 6,0 μg d'azote 13, émetteur \beta ^+, dans le sang du patient.
Une tomographie par émission de positons est effectuée sur un patient. Pour cela, on injecte 6,0 μg d'azote 13, émetteur \beta ^+, dans le sang du patient.
1. Écrire l'équation de désintégration de l'azote 13.
2. Expliquer en quoi le carbone 11 ou l'azote 12 qui émettent également des positons ne sont pas adaptés pour ce type d'examen.
Une analyse radioactive donne l'évolution de l'activité A en fonction du temps t :
| A (TBq) | 180 | 101 | 56,6 | 31,7 | |
| t (s) | 0 | 500 | 1 000 | 1 500 | 2 000 |
| A (TBq) | 17,8 | 9,96 | 5,58 | 3,13 | 1,75 |
| t (s) | 2 500 | 3 000 | 3 500 | 4 000 | 4 500 |
3. Déterminer le nombre initial de noyaux
radioactifs.
4. En déduire l'activité correspondante.
5. Tracer la courbe A = f(t).
4. En déduire l'activité correspondante.
5. Tracer la courbe A = f(t).
GeoGebra
6. Définir et déterminer le temps de demi-vie à partir de la courbe. Comparer votre résultat à la valeur théorique.
Données
- Masse molaire de l'azote 13 : M(^{13}\text{N}) = 13{,}0 g·mol-1
- Temps de demi-vie : t_{1/2}(^{13}\text{N}) = 9{,}97 min, t_{1/2}(^{12}\text{N}) = 11{,}0 ms et t_{1/2}(^{11}\text{C}) = 20{,}4 min
- Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23}mol-1
Détails du barème
TOTAL /6 pts
0,5 pt
1. Respecter les lois de Soddy.
0,5 pt
2. S'approprier le sujet.
0,5 pt
2. Faire preuve d'analyse.
1 pt
3. Réinvestir les notions connues.
1 pt
4. Appliquer directement le cours.
1,5 pt
5. Utiliser une échelle adaptée.
0,5 pt
6. Restituer le cours.
0,5 pt
6. Faire preuve d'exprit critique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Histoire d'uranium
✔ APP : Extraire l'information utile
Doc.
Population d'atomes d'uranium
Pour ce qui nous concerne, nous les uranium, [le temps de demi-vie] varie selon les isotopes. Normal,
nous n'avons pas le même nombre de neutrons, et donc pas le même degré de cohésion. La période
de l'uranium 238, qui a trois neutrons de plus que nous, vaut presque 5 milliards d'années [...]. Pour
nos cousins 234, qui ont un neutron de moins que nous, c'est seulement 245 000 ans, ce qui explique leur rareté dans vos mines terrestres.
[...] [Nos temps de demi-vie] sont très [longs], beaucoup plus [longs] que [celui] du polonium 214 (0,16 s), ou même que celui du carbone 14 (5 730 a). Ce qui signifie qu'il nous faut beaucoup de temps pour que nous consentions à diminuer notablement nos effectifs, et donc que nous sommes tous très faiblement… radioactifs.
[...] [Nos temps de demi-vie] sont très [longs], beaucoup plus [longs] que [celui] du polonium 214 (0,16 s), ou même que celui du carbone 14 (5 730 a). Ce qui signifie qu'il nous faut beaucoup de temps pour que nous consentions à diminuer notablement nos effectifs, et donc que nous sommes tous très faiblement… radioactifs.
1. Définir un noyau radioactif.
2. En utilisant cette définition et le texte ci-dessus, expliquer les différences de temps de demi-vie des noyaux radioactifs.
2. En utilisant cette définition et le texte ci-dessus, expliquer les différences de temps de demi-vie des noyaux radioactifs.
3. Donner la composition du noyau narrateur de ce texte.
4. Sachant que son temps de demi-vie est de 703,8 millions d'années, classer les trois isotopes de l'uranium cités par ordre de stabilité croissante.
4. Sachant que son temps de demi-vie est de 703,8 millions d'années, classer les trois isotopes de l'uranium cités par ordre de stabilité croissante.
5. Expliquer pourquoi l'uranium en général ne présente
que peu de danger comme noyau radioactif.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Tchernobyl
✔ APP : Faire des prévisions à l'aide d'un modèle
Le 26 avril 1986, une catastrophe nucléaire sans précédent s'est produite à Tchernobyl. L'accident a libéré d'importantes quantités de noyaux radioactifs dans l'air tels que le césium 137 et l'iode 131.
Le 26 avril 1986, une catastrophe nucléaire sans précédent s'est produite à Tchernobyl. L'accident a libéré d'importantes quantités de noyaux radioactifs dans l'air tels que le césium 137 et l'iode 131.
Données
- Masses molaires : M(^{137}\text{Cs}) = 136{,}9 g·mol-1 et
M(^{131}\text{I}) = 130{,}9 g·mol-1 - Temps de demi-vie : t_{1/2}(^{137}\text{Cs}) = 30{,}04 a et
t_{1/2}(^{131}\text{I}) = 8{,}02 j - Constante d'Avogadro : N_{\text{A}} = 6{,}02 \times 10^{23} mol-1
1.Donner la composition de ces noyaux.
2. L'iode 131 et le césium 137 ont une radioactivité de type \beta ^-, puis le noyau fils subit une désexcitation \gamma. Écrire les équations de désintégration.
3. Nommer les particules émises.
4. Calculer les constantes radioactives de ces isotopes.
2. L'iode 131 et le césium 137 ont une radioactivité de type \beta ^-, puis le noyau fils subit une désexcitation \gamma. Écrire les équations de désintégration.
3. Nommer les particules émises.
4. Calculer les constantes radioactives de ces isotopes.
5. Pour une même masse de 1,0 kg de déchets relâchés, déterminer le nombre de noyaux correspondant.
6. Déterminer l'activité massique de chaque isotope.
7. Calculer le nombre de noyaux non désintégrés aujourd'hui et en déduire l'activité massique.
8. Préciser lequel de ces isotopes est le plus dangereux à long terme.
6. Déterminer l'activité massique de chaque isotope.
7. Calculer le nombre de noyaux non désintégrés aujourd'hui et en déduire l'activité massique.
8. Préciser lequel de ces isotopes est le plus dangereux à long terme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Copie d'élève à commenter
Proposer une justification pour chaque erreur relevée par le correcteur.
Le polonium 210 est un poison très puissant à cause de ses émissions \alpha : 1 μg suffit à causer la mort. Une personne dont la mort est suspecte a été retrouvée avec une activité en polonium de 818 kBq. Les analyses ont été effectuées 72 h après sa mort.
Le polonium 210 est un poison très puissant à cause de ses émissions \alpha : 1 μg suffit à causer la mort. Une personne dont la mort est suspecte a été retrouvée avec une activité en polonium de 818 kBq. Les analyses ont été effectuées 72 h après sa mort.
1. Écrire l'équation de désintégration.
2. Déterminer le nombre de noyaux retrouvés.
L'équation de désintégration du polonium 210 est :
^{210}_{\thickspace84}\text{Po} \rightarrow \color{red}\xcancel{\color{black}{^{208}_{\thickspace80}\text{Hg} + \ ^2_1\text{He}}}
^{210}_{\thickspace84}\text{Po} \rightarrow \color{red}\xcancel{\color{black}{^{208}_{\thickspace80}\text{Hg} + \ ^2_1\text{He}}}
2. Déterminer le nombre de noyaux retrouvés.
La relation est la suivante :
N = \dfrac{A}{\lambda} = \dfrac{A \cdot t_{1/2}}{\ln(2)}
AN : N(t) = \dfrac{818 \times 10^3 \times \sout{138{,}4}}{\ln(2)} = \color{red}\xcancel{\color{black}{1{,}63 \times 10^8}}
N = \dfrac{A}{\lambda} = \dfrac{A \cdot t_{1/2}}{\ln(2)}
AN : N(t) = \dfrac{818 \times 10^3 \times \sout{138{,}4}}{\ln(2)} = \color{red}\xcancel{\color{black}{1{,}63 \times 10^8}}
3. En déduire le nombre et la masse de noyaux de polonium initiaux.
N(t) = N_0 \cdot \exp(-\lambda \cdot t)
N_0 = N(t) \cdot \exp(\lambda \cdot t)
N_0 = N(t) \cdot \exp \bigg(\dfrac{\ln(2) \cdot t}{t_{1/2}}\bigg)
AN : N_0 = 1{,}63 \times 10^8 \times \exp \bigg( \dfrac {\ln(2) \times 72} { \color{red}\xcancel{\color{black}{138{,}4}} } \bigg)
N_0 = \color{red}\xcancel{\color{black}{1{,}61 \times 10^8}}
La masse initiale de polonium vaut :
m = \dfrac{N_0}{N_{\text{A}}} \cdot M
AN : m = \dfrac{\color{red}\xcancel{\color{black}{1{,}61 \times 10^8}}}{6{,}02 \times 10^{23}} \times 210 = \color{red}\xcancel{\color{black}{5{,}61 \times 10^{23}}} g
N_0 = N(t) \cdot \exp(\lambda \cdot t)
N_0 = N(t) \cdot \exp \bigg(\dfrac{\ln(2) \cdot t}{t_{1/2}}\bigg)
AN : N_0 = 1{,}63 \times 10^8 \times \exp \bigg( \dfrac {\ln(2) \times 72} { \color{red}\xcancel{\color{black}{138{,}4}} } \bigg)
N_0 = \color{red}\xcancel{\color{black}{1{,}61 \times 10^8}}
La masse initiale de polonium vaut :
m = \dfrac{N_0}{N_{\text{A}}} \cdot M
AN : m = \dfrac{\color{red}\xcancel{\color{black}{1{,}61 \times 10^8}}}{6{,}02 \times 10^{23}} \times 210 = \color{red}\xcancel{\color{black}{5{,}61 \times 10^{23}}} g
Données
- Masse molaire du polonium 210 : M(^{210}\text{Po}) = 210{,}0 g·mol-1
- Temps de demi-vie du polonium 210 : t_{1/2}(^{210}\text{Po}) = 138{,}4 j
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
