Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 12
Exercices
Pour s'échauffer - Pour commencer
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Choix d'un bon référentiel
Pour chaque mouvement à étudier, choisir un référentiel qui puisse être considéré comme galiléen.
a. La rotation d'un satellite autour de la Terre.
b. Le lancer d'un javelot.
c. Le balancement d'un objet suspendu au rétroviseur d'une voiture.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Pendule
Préciser pourquoi la sphère de
masse m n'est pas à l'équilibre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Vecteur accélération
Une voiture de masse m = 1{,}0 \times 10^{3} kg est en accélération
sur une route rectiligne et horizontale. La résultante de
ses forces extérieures a pour intensité 800 N.
Lister les caractéristiques du vecteur accélération \overrightarrow{a}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Caillou
Un caillou tombe verticalement à l'intérieur d'un verre plein d'eau. Justifier si la chute est libre ou non.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9Vecteur vitesse initiale
Exprimer les coordonnées
du vecteur \overrightarrow{v}_{0} dans le repère
ci‑dessous.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Service au tennis
On considère un service au tennis en négligeant les frottements de l'air. Indiquer les caractéristiques du
vecteur accélération \overrightarrow{a} du centre de masse de la balle
une fois qu'elle n'est plus en contact avec la raquette.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Théorème de l'énergie cinétique
Justifier et proposer un exemple pour montrer qu'une variation d'énergie peut être négative.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour commencer
Équilibre d'un solide
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Hamac
✔ REA : Utiliser un modèle
Une personne est allongée dans un hamac suspendu entre deux arbres.
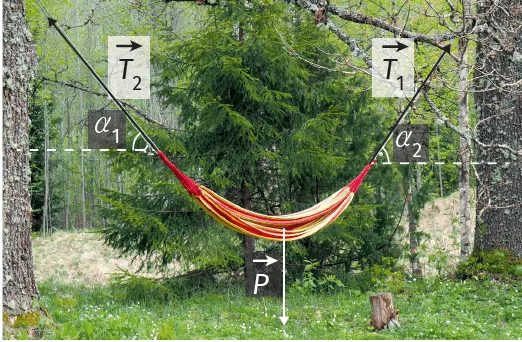
1. Écrire la condition d'équilibre du système.
1. Écrire la condition d'équilibre du système.
2. Projeter la relation précédente sur les axes d'un repère (\mathrm{O}, \overrightarrow{i}, \overrightarrow{j} ).
3. En déduire les normes des tensions des cordes \overrightarrow{T_{1}} et \overrightarrow{T_{2}} .
3. En déduire les normes des tensions des cordes \overrightarrow{T_{1}} et \overrightarrow{T_{2}} .
Données
- Masse de la personne et du hamac : m = 70 kg
- Intensité de pesanteur : g = 9{,}81 N·kg-1
- Angles considérés : \alpha_{1}=54^{\circ} et \alpha_{2}=50^{\circ}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Plan incliné
✔ APP : Extraire l'information utile
Un solide de masse m, à l'équilibre, est accroché à un ressort et repose sur un plan incliné d'un angle \alpha par rapport à l'horizontale.
Les trois forces qui s'exercent sur le solide sont : son poids \overrightarrow{P}, la tension du ressort \overrightarrow{T} et la réaction normale du support \overrightarrow{R}.
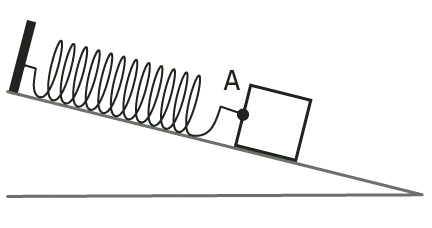
1. Représenter les forces s'exerçant sur le solide.
2. Calculer l'angle d'inclinaison \alpha de la pente.
3. Calculer la norme de la réaction du support.
3. Calculer la norme de la réaction du support.
Données
- Masse du solide : m = 250 g
- Intensité de pesanteur : g = 9{,}81 N·kg-1
- Tension du ressort : T = 1{,}25 N
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Deuxième loi de Newton
Deuxième loi de Newton
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Ascenseur
✔ REA : Appliquer une formule
La cabine d'un ascenseur de masse 1 \:200 kg se trouve au rez-de-chaussée et démarre pour monter dans les étages supérieurs. Son accélération est de 1{,}5 m·s-2, jusqu'à ce qu'elle atteigne une vitesse constante de 2{,}0 m·s-1.
1. Faire le bilan des forces exercées sur la cabine d'ascenseur dans le référentiel terrestre.
2. Appliquer la deuxième loi de Newton afin de déterminer la valeur de la tension T du câble qui permet à la cabine de s'élever.
2. Appliquer la deuxième loi de Newton afin de déterminer la valeur de la tension T du câble qui permet à la cabine de s'élever.
3. Déterminer la valeur de la tension lorsque la vitesse devient constante.
Donnée
- Intensité de pesanteur : g = 9{,}81 N·kg-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15Descente en luge
✔ APP : Faire un schéma
Un enfant est assis sur une luge immobile en haut d'une pente enneigée, inclinée d'un angle \alpha = 15°.
1. Représenter sur l'image les forces qui s'exercent sur le système constitué par l'enfant et sa luge.
Crédits : Drop of Light/Shutterstock
2. Déterminer l'intensité
de la force de frottement f exercée par la neige sur la luge afin que le système formé par l'enfant et la luge reste immobile.
Un adulte pousse l'enfant afin de lui permettre de s'élancer. Une fois que la luge glisse seule, la force de frottement s'exerçant pendant la descente a pour valeur :
Un adulte pousse l'enfant afin de lui permettre de s'élancer. Une fois que la luge glisse seule, la force de frottement s'exerçant pendant la descente a pour valeur :
f=k\cdot R
k : coefficient de frottement égal à 0{,}80
R : réaction normale de la pente (N)
R : réaction normale de la pente (N)
3.
a. En considérant que la luge reste toujours en contact avec la pente, déterminer la valeur de la réaction de la pente \overrightarrow{R}.
b. En déduire la valeur de la force de frottement \overrightarrow{f}.
c. Déterminer les caractéristiques du vecteur accélération \overrightarrow{a} du système.
d. Préciser la nature du mouvement.
b. En déduire la valeur de la force de frottement \overrightarrow{f}.
c. Déterminer les caractéristiques du vecteur accélération \overrightarrow{a} du système.
d. Préciser la nature du mouvement.
Données
- Masse de l'enfant et de la luge : m = 38 kg
- Intensité de pesanteur : g = 9{,}81 N·kg-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Chute libre
Chute libre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Plume et marteau
✔ REA/MATH : Intégrer
Lors de la mission Apollo 15, en 1971, les astronautes séjournent sur la Lune durant près de 64 heures et y réalisent différentes expériences. Peu avant la fin de la mission, David Scott prend dans chaque main une plume et un marteau afin de vérifier la loi de la chute des corps de Galilée. Il les lâche au même instant : la plume et le marteau touchent le sol lunaire simultanément, 1{,}2 s plus tard.
L'axe (\text Oz) est dirigé vers le bas et son origine \text{O} est confondue avec le centre de masse du marteau à l'instant du lâcher.
1. Préciser le référentiel d'étude.
2. Appliquer la deuxième loi de Newton à chaque objet et montrer qu'ils ont le même vecteur accélération.
3. En déduire l'expression de la composante verticale v_{z}(t), puis celle de z(t).
4. Exprimer g_{\mathrm{L}}, l'intensité de pesanteur sur la Lune, en fonction du temps de chute t_{\mathrm{c}} et de la hauteur de chute h.
5. Utiliser le doc. suivant pour estimer h, et en déduire la valeur de g_{\mathrm{L}}.
6. La valeur de g_{\mathrm{L}} est en réalité de 1{,}62 N·kg-1.
Commenter l'éventuel écart constaté.
2. Appliquer la deuxième loi de Newton à chaque objet et montrer qu'ils ont le même vecteur accélération.
3. En déduire l'expression de la composante verticale v_{z}(t), puis celle de z(t).
4. Exprimer g_{\mathrm{L}}, l'intensité de pesanteur sur la Lune, en fonction du temps de chute t_{\mathrm{c}} et de la hauteur de chute h.
5. Utiliser le doc. suivant pour estimer h, et en déduire la valeur de g_{\mathrm{L}}.
6. La valeur de g_{\mathrm{L}} est en réalité de 1{,}62 N·kg-1.
Commenter l'éventuel écart constaté.
Donnée
- Taille de David Scott : l = 1{,}84 m
Doc.
Expérience de David Scott
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Détermination d'une vitesse initiale
✔ REA/MATH : Intégrer
Avant de réaliser un service, une joueuse de tennis lance sa balle verticalement vers le haut.
Son point de lancement est pris comme origine d'un axe vertical dirigé vers le haut. On assimilera la balle à son centre de masse \text{G}.
1. Établir l'expression de
la composante v_{z}(t) de la vitesse de la balle.
2. Établir l'équation horaire z(t) du mouvement de la balle.
3. Calculer la valeur de la vitesse initiale que la joueuse doit communiquer à la balle si elle veut qu'elle s'élève de 2,0 m par rapport à sa position initiale.
2. Établir l'équation horaire z(t) du mouvement de la balle.
3. Calculer la valeur de la vitesse initiale que la joueuse doit communiquer à la balle si elle veut qu'elle s'élève de 2,0 m par rapport à sa position initiale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Représentation des équations horaires
✔ VAL : Analyser des résultats
Lors d'une séance de travaux pratiques, des élèves ont travaillé sur la vidéo d'un tir au but et réalisé le pointage. Ils ont ensuite tracé les équations horaires du mouvement du centre de masse du ballon, x(t) et y(t), puis obtenu et tracé v_{x}(t) et v_{y}(t). Contents de leur travail, ils ont imprimé les graphiques obtenus... sans indiquer les noms et les unités des axes !
Afin de les aider, leur professeur leur rappelle que :
\overrightarrow{v}\left(\begin{array}{l}
v_{x}(t)=v_{0} · \cos (\alpha) \\
v_{y}(t)=-g · t+v_{0} · \sin (\alpha)
\end{array}\right)_{(\mathrm{O}, \overrightarrow{i}, \overrightarrow{j})}
1. Déterminer les expressions de x(t) et y(t).
2. Associer chaque graphique à l'équation correspondante.
Graphique 1 :
Graphique 2 :
Graphique 2 :
Graphique 3 :
Graphique 4 :
Graphique 4 :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ACycliste 1
✔ RAI/MOD : Utiliser avec rigueur le modèle de l'énergie
Un cycliste est en haut d'une pente, il se laisse entraîner par son poids, sans pédaler. La masse du cycliste et du vélo réunis est de 80 kg. Il part avec une vitesse nulle, et en bas de la pente il atteint une vitesse de 34 km·h-1. On néglige tout frottement.
Un cycliste est en haut d'une pente, il se laisse entraîner par son poids, sans pédaler. La masse du cycliste et du vélo réunis est de 80 kg. Il part avec une vitesse nulle, et en bas de la pente il atteint une vitesse de 34 km·h-1. On néglige tout frottement.
1. Calculer la variation d'énergie cinétique.
2. Déterminer la différence d'altitude.
2. Déterminer la différence d'altitude.
3. En bas de la descente, il arrive sur une zone plate et rencontre un panneau « Stop », il freine brutalement et s'arrête. Calculer le travail de la force exercée par les freins.
Donnée
- Intensité de la pesanteur terrestre : g = 9{,}81 N·kg-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCycliste 2
✔ RAI/MOD : Utiliser avec rigueur le modèle de l'énergie
Après une ligne droite, le même cycliste grimpe une côte. Il commence son ascension à une vitesse de 32 km·h-1, et atteint le col, 76 m plus haut, à une vitesse de 8,0 km·h-1. On néglige tout frottement.
Après une ligne droite, le même cycliste grimpe une côte. Il commence son ascension à une vitesse de 32 km·h-1, et atteint le col, 76 m plus haut, à une vitesse de 8,0 km·h-1. On néglige tout frottement.
1. Calculer la variation d'énergie cinétique.
2. Calculer le travail du poids.
2. Calculer le travail du poids.
3. Calculer le travail qu'a dû fournir le cycliste en pédalant.
Données
- Masse du cycliste et de son vélo : m = 80 kg
- Intensité de pesanteur terrestre : g = 9{,}81 N·kg-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Particule dans un champ électrique
Particule dans un champ électrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Accélération d'un électron
✔ APP : Faire des hypothèses
Un faisceau d'électrons est émis dans le vide par un filament
avec une vitesse initiale négligeable. Il est accéléré
par une tension U de valeur absolue 200 V appliquée
entre deux plaques A et B. La distance entre les plaques
est d = 4{,}0 cm. La plaque B est percée d'un trou noté O.
1. Préciser le signe de la tension U pour que l'électron soit accéléré.
2. Exprimer la valeur et préciser la direction et le sens du champ électrique \overrightarrow{E} régnant entre les plaques A et B.
On considère qu'une force est négligeable devant une autre si son intensité est au moins 103 fois plus petite.
3. Montrer que le poids de l'électron est négligeable devant la force électrique.
4. Calculer la vitesse de l'électron lorsqu'il arrive au point \text{O}.
2. Exprimer la valeur et préciser la direction et le sens du champ électrique \overrightarrow{E} régnant entre les plaques A et B.
On considère qu'une force est négligeable devant une autre si son intensité est au moins 103 fois plus petite.
3. Montrer que le poids de l'électron est négligeable devant la force électrique.
4. Calculer la vitesse de l'électron lorsqu'il arrive au point \text{O}.
Données
- Intensité de pesanteur : g = 9{,}81 N·kg-1
- Masse de l'électron : m_{e} = 9{,}11 \times 10^{-31} kg
- Charge élémentaire : e = 1{,}60 \times 10^{-19} C
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Déviation d'une particule
✔ APP : Faire des prévisions à l'aide d'un modèle
Une particule chargée positivement pénètre
dans un champ électrique uniforme créé
entre les plaques d'un condensateur plan.
Sur la figure ci‑dessous, on a représenté la vitesse initiale de la particule ainsi qu'une partie de sa trajectoire.
Sur la figure ci‑dessous, on a représenté la vitesse initiale de la particule ainsi qu'une partie de sa trajectoire.
2. Indiquer le signe des charges de chacune des plaques.
3. Définir la trajectoire si le vecteur \overrightarrow{v}_{0} était perpendiculaire aux plaques.
4. Préciser quelle serait la trajectoire avec une particule chargée négativement.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercices
Différenciation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21 Jeu de fête foraine (1)
✔ RAI/MOD : Utiliser avec rigueur le modèle de l'énergie
D'après le sujet Bac S, Antilles, 2005.
Un jeu de fête foraine a pour but d'envoyer une bille dans un trou. Afin de la lancer, le joueur comprime un ressort. La bille roule ensuite horizontalement sans frottements. Le ressort emmagasine une énergie potentielle élastique :
E_{\mathrm{pe}}=\frac{1}{2} k\ · \Delta l^{2}
E_{\mathrm{pe}} : énergie potentielle élastique (J)
k : constante de raideur du ressort (N·m-1)
\Delta l : variation de longueur (m)
1. Calculer l'énergie potentielle élastique E_{\mathrm{pe}}.
2. Préciser la forme d'énergie acquise par la bille éjectée.
3. Calculer la valeur de la vitesse au point \text{C}.
2. Préciser la forme d'énergie acquise par la bille éjectée.
3. Calculer la valeur de la vitesse au point \text{C}.
Données
- Raideur du ressort : k = 25 N·m-1
- Variation de longueur du ressort : \Delta l=-10 cm
- Masse de la bille : m = 10 g
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22 Jeu de fête foraine (2)
✔ RAI/MOD : Utiliser avec rigueur le modèle de l'énergie
Un jeu de fête foraine consiste à lancer une bille depuis
un point A le long d'un rail. L'objectif est de lui faire faire
un looping sur une portion circulaire de rayon r.
1. Préciser l'altitude z_{max} que doit remonter la bille sur la portion circulaire afin que le looping soit réussi.
1. Préciser l'altitude z_{max} que doit remonter la bille sur la portion circulaire afin que le looping soit réussi.
2. En déduire la hauteur h de la bille depuis laquelle
elle devrait être lâchée en A sans vitesse initiale.
3. En considérant cette fois-ci une hauteur de lâcher initiale égale à h = 0{,}75 m et un rayon de la boucle égale à 50 cm, déterminer la vitesse v_{min} que doit lui donner le joueur afin qu'il réussisse le looping.
3. En considérant cette fois-ci une hauteur de lâcher initiale égale à h = 0{,}75 m et un rayon de la boucle égale à 50 cm, déterminer la vitesse v_{min} que doit lui donner le joueur afin qu'il réussisse le looping.
Donnée
- Intensité de pesanteur : g = 9{,}81 N·kg-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23 Lancer d'une bille de flipper
✔ RAI/MOD : Utiliser avec rigueur le modèle de l'énergie
D'après le sujet Bac Antilles/Guyane, septembre 2018.
Au début d'une partie de flipper, le joueur actionne une poignée qui comprime un ressort pour propulser la bille.
On souhaite s'assurer qu'un ressort choisi pour fabriquer un flipper permettra bien à la bille d'atteindre l'extrémité de la rampe de lancement.
Au début d'une partie de flipper, le joueur actionne une poignée qui comprime un ressort pour propulser la bille.
On souhaite s'assurer qu'un ressort choisi pour fabriquer un flipper permettra bien à la bille d'atteindre l'extrémité de la rampe de lancement.
1. Montrer que l'énergie potentielle élastique E_{\mathrm{p e}}
emmagasinée par le ressort est suffisante pour
permettre à la bille d'atteindre l'extrémité de la
rampe de lancement.
2. Calculer la vitesse alors atteinte par la bille.
E_{\mathrm{p e}}=\frac{1}{2} k · \Delta l^{2}
E_{\mathrm{pe}} : énergie potentielle élastique (J)
k : constante de raideur du ressort (N·m-1)
\Delta l : variation de longueur (m)
2. Calculer la vitesse alors atteinte par la bille.
Doc.
Énergie potentielle élastique
Pour un ressort, on peut considérer que l'énergie
potentielle élastique emmagasinée s'écrit :
E_{\mathrm{p e}}=\frac{1}{2} k · \Delta l^{2}
E_{\mathrm{pe}} : énergie potentielle élastique (J)
k : constante de raideur du ressort (N·m-1)
\Delta l : variation de longueur (m)
Données
- Raideur du ressort du flipper : k = 33 N·m-1
- Intensité de pesanteur : g = 9{,}81 N·kg-1
- Variation de longueur du ressort : \Delta l=90 mm
- Masse de la bille : m = 100 g
- Hauteur de la rampe de lancement : h = 10 cm
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
