Physique-Chimie Terminale Spécialité
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 13
Cours
Mouvement dans un champ de gravitation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Lois de Kepler
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Malgré la révolution copernicienne du XVIe siècle, lors du passage du référentiel géocentrique au référentiel héliocentrique, le nouveau modèle s'avère insuffisant pour expliquer la trajectoire de la planète Mars. Afin d'expliquer son mouvement rétrograde, J. Kepler établit trois lois qu'il généralise aux autres planètes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
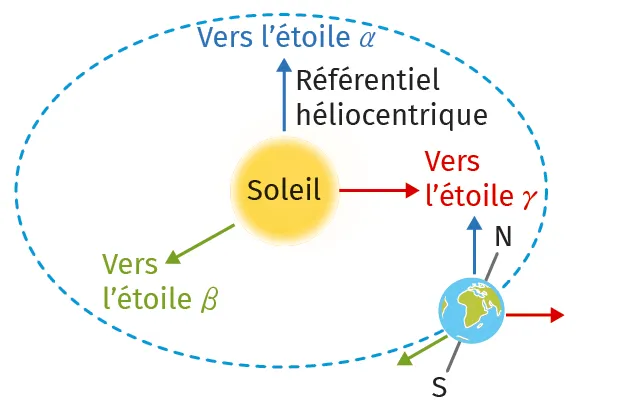
Doc. 1Référentiel héliocentrique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ALoi des orbites : première loi de Kepler
Dans le référentiel héliocentrique, la trajectoire d'une planète est décrite par une orbite elliptique dont le Soleil est l'un des foyers.
- le référentiel héliocentrique : référentiel associé à un repère spatial dont l'origine est le centre de masse du Soleil et dont les trois axes sont dirigés vers des étoiles lointaines ;
- l'orbite : trajectoire dessinée dans l'espace par le système étudié, assimilé à un point matériel sous l'effet de la gravitation ;
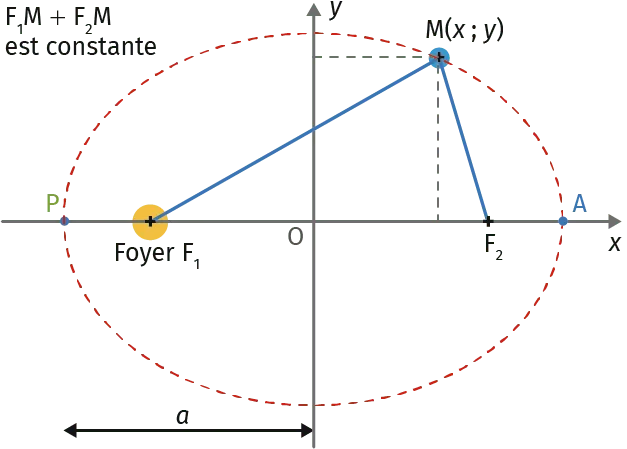
- ellipse : ensemble des points \text{M} dont la somme des distances (\text{F}_1\text{M}, \text{F}_2\text{M}) à deux points fixes (\text{F}_1, \text{F}_2) est constante. Si \text{F}_1 et \text{F}_2 sont confondus en un point \text{O}, l'ellipse est alors un cercle.
Les orbites des planètes sont considérées être dans le plan écliptique, plan géométrique contenant l'orbite de la Terre autour du Soleil.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Propriétés d'une ellipse
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
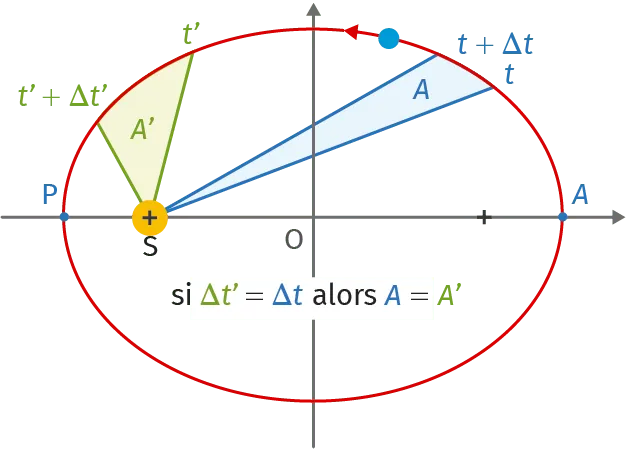
Doc. 3Loi des aires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BLoi des aires : deuxième loi de Kepler
Dans le référentiel héliocentrique, le segment reliant le centre du Soleil au centre de la planète balaie des aires égales \left(A_{1}=A_{2}\right) au cours de durées égales \left(\Delta t_{1}=\Delta t_{2}\right).
Cette loi implique alors que la norme du vecteur vitesse d'une planète n'est pas constante au cours de sa révolution. Elle augmente ou diminue selon que la planète se rapproche ou s'éloigne du Soleil.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Péri ou apo‑astre
Péri ou apo‑astre : point de l'orbite d'un objet céleste où la distance est minimale/maximale entre deux corps.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLoi des périodes : troisième loi de Kepler
Le carré de la durée de la période d'une révolution T, d'une planète est proportionnel au cube du demi‑grand axe de l'ellipse a (doc. 2).
Soit la relation :
T^{2}=k \cdot a^{3}
T^{2}=k \cdot a^{3}
T : période de révolution de l'arbre en orbite (s)
k : constante dépendant de l'astre attracteur (s2·m-3)
a : demi-grand axe (m)
k : constante dépendant de l'astre attracteur (s2·m-3)
a : demi-grand axe (m)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ne pas confondre la période de révolution avec la période de rotation (sur elle‑même) d'une planète.
Par exemple, on estime, pour la Terre :
Par exemple, on estime, pour la Terre :
- période rotation : 24 h ;
- période de révolution : 365,25 j.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Mouvement d'un satellite
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
L'approximation de l'orbite par une trajectoire circulaire simplifie le
modèle. Dans ce cas, les deux premières lois de Kepler indiquent que :
- l'orbite est un cercle dont le demi-grand axe correspond au rayon r. Les deux foyers sont confondus avec le centre du cercle ;
- la vitesse du satellite est constante durant sa révolution.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 4Représentation des vecteurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
APosition du problème
On considère un satellite \text{S} de masse m_{\mathrm{s}}, en orbite autour de la Terre, notée \text{T}, de masse M_\text{T}. Tous deux sont considérés comme ponctuels et associés à leur centre de masse \text{G} et \text{O}. Le référentiel est géocentrique, supposé galiléen.
Le satellite n'est alors soumis qu'à la force d'interaction gravitationnelle terrestre dont on rappelle l'expression vectorielle :
On peut exprimer cette force selon le vecteur \vec{N} du repère de Frenet \nobreakspace{(G, \vec{T}, \vec{N})} avec les propriétés associées :
Le satellite n'est alors soumis qu'à la force d'interaction gravitationnelle terrestre dont on rappelle l'expression vectorielle :
\overrightarrow{F_{\mathrm{T} / \mathrm{s}}}=-G \cdot \frac{m_{\mathrm{S}} \cdot M_{\mathrm{T}}}{r^{2}} \cdot \vec{u}
\overrightarrow{F_{\mathrm{T} / \mathrm{s}}} : force d'interaction gravitationnelle exercée par la Terre sur le satellite (N)
G : constante de gravitation universelle égale à G=6{,}67 \times 10^{-11} N·m2·kg-2
m_\text{S} et M_\text{T} : masse du satellite et de la Terre (kg)
r : distance entre les centres \text{G} et \text{O} (m)
\overrightarrow{u} : vecteur unitaire dirigé de la Terre vers le satellite
G : constante de gravitation universelle égale à G=6{,}67 \times 10^{-11} N·m2·kg-2
m_\text{S} et M_\text{T} : masse du satellite et de la Terre (kg)
r : distance entre les centres \text{G} et \text{O} (m)
\overrightarrow{u} : vecteur unitaire dirigé de la Terre vers le satellite
\overrightarrow{F_{\mathrm{T} / \mathrm{S}}}=-\overrightarrow{F_{\mathrm{S} / \mathrm{T}}}=G \cdot \frac{m_{\mathrm{S}} \cdot M_{\mathrm{T}}}{r^{2}} \cdot \vec{N}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Attention à l'éventuel signe négatif dans l'expression de l'interaction gravitationnelle suivant l'orientation du vecteur unitaire de référence.
- Ne pas oublier de représenter graphiquement les forces à l'aide de vecteurs.
- Ne pas confondre valeur et expression vectorielle d'une force.
- Attention à ne pas confondre le rayon r de l'orbite avec l'altitude h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 5Accélération \boldsymbol{(\vec{N}, \vec{T})}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BVecteurs vitesse et accélération
Le référentiel d'étude géocentrique étant supposé galiléen, la deuxième loi de Newton peut s'appliquer au satellite :
\overrightarrow{F_{\mathrm{T} / \mathrm{S}}}=m_{\mathrm{S}} \cdot \vec{a}
\vec{a}=G \cdot \frac{M_{T}}{r^{2}} \cdot \vec{N}
En utilisant l'expression de a dans le repère de Frenet, on a :
\vec{a}\left(\begin{array}{c} \frac{\text{d} v}{\text{d} t} \\ \frac{v^{2}}{r} \end{array}\right)_{(G, \vec{T}, \vec{N})}
On obtient par identification :
\frac{v^{2}}{r}=G \cdot \frac{M_{T}}{r^{2}} \text { et } \frac{\text{d} v}{\text{d} t}=0
On peut donc en déduire que la vitesse du satellite est constante, car a_{\mathrm{T}}=0 m•s-2 et que l'intensité de la vitesse est égale à :
\overrightarrow{F_{\mathrm{T} / \mathrm{S}}}=m_{\mathrm{S}} \cdot \vec{a}
\vec{a}=G \cdot \frac{M_{T}}{r^{2}} \cdot \vec{N}
En utilisant l'expression de a dans le repère de Frenet, on a :
\vec{a}\left(\begin{array}{c} \frac{\text{d} v}{\text{d} t} \\ \frac{v^{2}}{r} \end{array}\right)_{(G, \vec{T}, \vec{N})}
On obtient par identification :
\frac{v^{2}}{r}=G \cdot \frac{M_{T}}{r^{2}} \text { et } \frac{\text{d} v}{\text{d} t}=0
On peut donc en déduire que la vitesse du satellite est constante, car a_{\mathrm{T}}=0 m•s-2 et que l'intensité de la vitesse est égale à :
v=\sqrt{\dfrac{G \cdot M_{T}}{r}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Le vecteur vitesse \vec{v} du satellite est toujours tangent à sa trajectoire.
- Le vecteur \vec{v} n'est pas constant sur la trajectoire, car sa direction change durant la révolution. Mais son intensité v reste constante sur une orbite de rayon r donnée.
- Comme le vecteur accélération \vec{a} est orienté vers le centre de masse de l'objet attracteur, il est centripète et non centrifuge.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CExpression de la troisième loi de Kepler
Dans le cas d'un mouvement circulaire de rayon r et uniforme du
satellite de période de révolution T autour de la Terre, on a :
En identifiant les deux expressions vitesses, on obtient :
\frac{2 \pi \cdot r}{T}=\sqrt{\frac{G \cdot M_{T}}{r}}
\frac{4 \pi^{2} \cdot r^{2}}{T^{2}}=\frac{G \cdot M_{T}}{r}
On retrouve bien la troisième loi de Kepler tel que T^2 est proportionnelle à r^3.
v=\frac{2 \pi \cdot r}{T}
En identifiant les deux expressions vitesses, on obtient :
\frac{2 \pi \cdot r}{T}=\sqrt{\frac{G \cdot M_{T}}{r}}
\frac{4 \pi^{2} \cdot r^{2}}{T^{2}}=\frac{G \cdot M_{T}}{r}
\frac{T^{2}}{r^{3}}=\frac{4 \pi^{2}}{G \cdot M_{\mathrm{T}}}
On retrouve bien la troisième loi de Kepler tel que T^2 est proportionnelle à r^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 6Relation de proportionnalité
Pour des satellites en orbite autour du même astre central :
\frac{T_{1}^{2}}{r_{1}^{3}}=\frac{T_{2}^{2}}{r_{2}^{3}}=\ldots=\frac{T_{\mathrm{n}}^{2}}{r_{\mathrm{n}}^{3}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez une explication de la force gravitationnelle en vidéo :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Satellite géostationnaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
De nombreux satellites artificiels mis en orbite autour de la Terre sont placés en orbite géostationnaire pour assurer diverses missions.
Le satellite géostationnaire semble immobile pour un observateur terrestre. En effet, sa période de révolution T_\text{s} est égale à la période de rotation de la Terre, soit 23 h 56 min 20 s (jour sidéral), soit 86 140 s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Jour sidéral
Jour solaire moyen
Jour sidéral : durée nécessaire à la Terre pour réaliser une rotation complète sur elle‑même.
Jour solaire moyen : durée qui sépare deux passages successifs du Soleil à la verticale d'un même lieu, soit 24 h = 86 400 s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application
Déterminer l'altitude des satellites géostationnaires à l'aide de la 3e loi de Kepler.
Corrigé
Le rayon de l'orbite est égal à r=R_{\mathrm{T}}+h, d'où :
r^{3}=G \cdot M_{T} \cdot \frac{T_{s}^{2}}{4 \pi^{2}}
r=\sqrt[3]{G \cdot M_{T} \cdot \frac{T_{s}^{2}}{4 \pi^{2}}}
En remplaçant r :
h=\sqrt[3]{G \cdot M_{T} \cdot \frac{T_{s}^{2}}{4 \pi^{2}}}-R_{T}
AN : h=\sqrt[3]{6,67 \times 10^{-11} \times 5{,}97 \times 10^{24} \times \dfrac{86\ 140^{2}}{4 \times \pi^{2}}}-6{,}37 \times 10^{6}
h=3{,}58 \times 10^{7} m
r^{3}=G \cdot M_{T} \cdot \frac{T_{s}^{2}}{4 \pi^{2}}
r=\sqrt[3]{G \cdot M_{T} \cdot \frac{T_{s}^{2}}{4 \pi^{2}}}
En remplaçant r :
h=\sqrt[3]{G \cdot M_{T} \cdot \frac{T_{s}^{2}}{4 \pi^{2}}}-R_{T}
AN : h=\sqrt[3]{6,67 \times 10^{-11} \times 5{,}97 \times 10^{24} \times \dfrac{86\ 140^{2}}{4 \times \pi^{2}}}-6{,}37 \times 10^{6}
h=3{,}58 \times 10^{7} m
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Un satellite en orbite géostationnaire évolue :
- suivant une orbite circulaire d'altitude environ égale à 36 000 km ;
- dans le plan équatorial terrestre ;
- en restant sur la même verticale passant par un point de la surface de la Terre.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Constante de gravitation universelle : G=6{,}67 \times 10^{-11} m3·kg-1·s-2
- Rayon de la Terre : R_{\text{T}}=6\, 370 km
- Masse de la Terre : M_{\mathrm{T}}=5{,}97 \times 10^{24} kg
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- Attention à bien convertir les distances en mètre (m), les durées en seconde (s) et les masses en kilogramme (kg).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 7Satellites MTG-S et MTG-I
Illustration de satellites géostationnaires.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
