Chapitre 6
Exercices
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je me teste
Je sais
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1Un parachutiste saute d'un hélicoptère. Il descend verticalement et sa vitesse augmente. Son mouvement est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2Dans une grande roue, quand la rotation s'effectue à vitesse constante, le mouvement est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3Un train démarre dans une gare. Par rapport à un passager qui regarde par la fenêtre, la gare :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4Rectiligne et/ou uniforme.
1. Relie les mouvements suivants avec la (ou les) caractéristique(s) associée(s).
| Hélice d'un avion prêt pour le décollage. | |
| Chute d'une goutte d'eau dans de l'huile. | |
| Chute d'un sauteur à l'élastique. |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5Les mots du mouvement.
Les mots suivants sont relatifs à l'étude du mouvement, sauf un. Lequel ?
Uniforme - moyenne - rectiligne - vitesse - volume - circulaire - instantanée - observateur.
Uniforme - moyenne - rectiligne - vitesse - volume - circulaire - instantanée - observateur.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6Complète la grille de mots-croisés.
Horizontal :
1. Déplacement.
2. Qui dépend de l'observateur.
1. Déplacement.
2. Qui dépend de l'observateur.
Vertical :
3. Quand la vitesse est constante.
4. Rapport entre la distance et le temps.
5. Vitesse calculée pour l'ensemble d'un trajet.
3. Quand la vitesse est constante.
4. Rapport entre la distance et le temps.
5. Vitesse calculée pour l'ensemble d'un trajet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je sais faire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7Certaines autruches peuvent atteindre la vitesse de 72 km/h. Quelle est la vitesse en m/s (arrondie au dixième) ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8Une automobile parcourt 500 mètres en 30 secondes. Sa vitesse est de :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9La relation qui permet de calculer la distance d, connaissant la vitesse v et le temps t est :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice corrigé
Compétence : Pratiquer le calcul numérique et le calcul littéral.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10Dans un TGV.
Dans un TGV lancé à pleine vitesse, Lucas observe les repères placés le long des voies et constate qu'il parcourt 7 km en 1 min et 26 s.
1. Calcule la vitesse du train en m/s (arrondie au dixième) puis en km/h (arrondie à l'unité).
1. Calcule la vitesse du train en m/s (arrondie au dixième) puis en km/h (arrondie à l'unité).


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Étapes de la méthode
- Pour convertir les unités de durée : on sait combien de secondes constituent 1 heure : 3 600. Donc on en déduit quelle fraction d'heure vaut 1 seconde : \dfrac{1}{3\:600}.
On multiplie alors cette fraction par le nombre de secondes. - Pour convertir les unités de distance : On sait combien de mètres vaut 1 kilomètre. Donc on en déduit le nombre de mètres en multipliant la distance en kilomètres par ce nombre : 1 000.
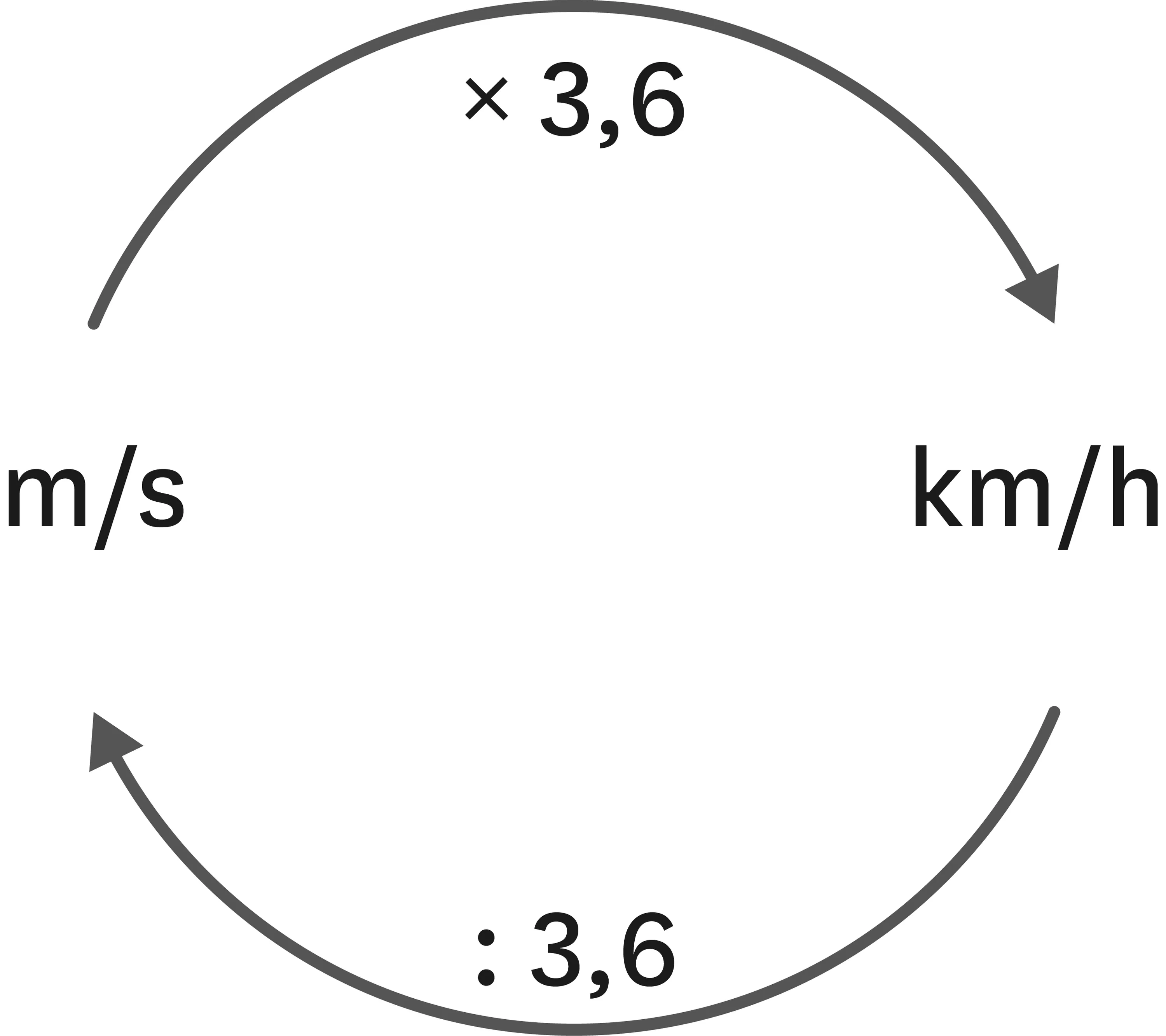
- Il peut être intéressant de connaitre directement la relation de proportionnalité entre les km/h et les m/s :
\dfrac{\text{km}}{\text{h}} = \dfrac{1\:000 \text{m}}{3\:600 \text{s}} = \dfrac{1 \text{m}}{3\text{,}6 \text{s}}.
Donc \dfrac{\text{vitesse en km/h}}{3\text{,}6} = vitesse en m/s, et inversement vitesse en km/h = 3,6 (vitesse en m/s).

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Corrigé
1. On utilise la relation v = \dfrac{d}{t}.
- En m/s :
On a la distance d = 7 km = 7 000 m
et la durée t = 1 min 16 s = 60 s + 26 s = 86 s.
Donc v = \dfrac{7\:000}{86} = 81\text{,}4 \dfrac{\text{m}}{\text{s}} (valeur arrondie au dixième). - En km/h :
On a la distance d = 7 km
et la durée d = 86 s = 86 \times \dfrac{1\text{h}}{3\:600} = 0\text{,}0239 h.
Donc v = \dfrac{7}{0\text{,}0239} = 293 km/h (valeur arrondie à l'unité).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercice similaire
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11Le voyage du module lunaire.
Lors de la mission Apollo 11, les astronautes ont voyagé pendant 72 h 35 min pour parcourir les 380 000 km de la distance Terre-Lune.
1. Calcule la vitesse de leur module lumière en m/s (valeur arrondie au dixième) et en km/h (valeur arrondie à l'unité).
1. Calcule la vitesse de leur module lumière en m/s (valeur arrondie au dixième) et en km/h (valeur arrondie à l'unité).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12Porte-avion.
Sur un porte-avion, l'appareil passe de 0 à 270 km/h en quelques secondes lors de son catapultage.
1. Le mouvement est-il rectiligne ? Est-il uniforme ? Justifie chaque réponse.
1. Le mouvement est-il rectiligne ? Est-il uniforme ? Justifie chaque réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13Voile.
Grâce au vent, un voilier se déplace en ligne droite à la vitesse de 18 km/h pendant 10 minutes.
1. Caractérise son mouvement.
2. Calcule la distance parcourue.
1. Caractérise son mouvement.
2. Calcule la distance parcourue.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14Dans un train.
Compétence
Mettre en œuvre un raisonnement logique simple pour résoudre un problème.
Jef se trouve en gare dans un TGV et regarde un autre train à côté du sien.
1. Soudain, il constate que ce deuxième train entre en mouvement mais il ne sait pas lequel se déplace vraiment. Pour quelle raison ?
2. Le deuxième train ayant « disparu », il se rend compte que c'est le sien qui se déplace car c'est maintenant le quai qui défile. Explique le raisonnement qui lui permet de faire cette déduction et caractérise le mouvement dans cette phase de démarrage au niveau du quai.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15Abysses.
Le son se propage à 1 500 m/s dans l'eau de mer. La fosse des Mariannes se situe à une profondeur de 11 km.
1. Calcule la durée d'une onde de sonar pour faire l'aller-retour entre la surface et le fond de la fosse qui réfléchit cette onde.
1. Calcule la durée d'une onde de sonar pour faire l'aller-retour entre la surface et le fond de la fosse qui réfléchit cette onde.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16Voyage vers Mars.
La distance entre la Terre et Mars évolue entre 56 millions et 400 millions de kilomètres. Un vaisseau spatial a une vitesse moyenne de 3 600 m/s (en tenant compte des phases d'accélération et de décélération dans cette moyenne).
1. Calcule, dans les deux cas, la durée (en jours) mis par le vaisseau pour parcourir la distance Terre-Mars. Fais attention aux unités.
1. Calcule, dans les deux cas, la durée (en jours) mis par le vaisseau pour parcourir la distance Terre-Mars. Fais attention aux unités.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17Vrai/faux.
Vérifie les égalités suivantes, et corrige celles qui sont fausses.
1. 120 s = 3 min.
2. 35 min 16 s = 2 116 s.
3. 1 h 30 min = 1,5 h.
4. 3 348 s = 0,93 h.
5. 45 min = 1/2 h.
6. 2,4 h = 2 h 24 min.
1. 120 s = 3 min.
2. 35 min 16 s = 2 116 s.
3. 1 h 30 min = 1,5 h.
4. 3 348 s = 0,93 h.
5. 45 min = 1/2 h.
6. 2,4 h = 2 h 24 min.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18Influx nerveux.
En 1852, Hermann Von Helmholtz réalise la mesure de la vitesse de l'influx nerveux à l'aide d'une grenouille. Il excite un nerf de 50 mm de longueur. L'irritation nerveuse met 0,0020 seconde pour parcourir la distance.
1. Calcule sa vitesse en m/s.
1. Calcule sa vitesse en m/s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19Escargot.
Un escargot repère une salade et fonce vers elle. Elle est à 0,8 m de lui, il lui faut 9 min 36 s avant de la déguster.
1. Calcule sa vitesse en m/s puis en km/h.
1. Calcule sa vitesse en m/s puis en km/h.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20Conversions.
Effectue les conversions suivantes.
1. 25 cm = m.
2. 2 015,3 mm = m.
3. 84,2 m = km.
4. 3 min = s.
5. 1 h 12 min = s.
6. 2 h 45 = h.
7. 215 s = h.
8. 12 min = h.
9. 1,35 h = h min.
1. 25 cm =
2. 2 015,3 mm =
3. 84,2 m =
4. 3 min =
5. 1 h 12 min =
6. 2 h 45 =
7. 215 s =
8. 12 min =
9. 1,35 h =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21Relation pour calculer la vitesse.
1. Rappelle la relation permettant de calculer la vitesse si l'on connait la distance parcourue et la durée du parcours.
2. Utilise cette relation pour calculer en 150 km/h la vitesse d'une automobile qui parcourt, à vitesse constante sur l'autoroute, 150 km en 1 h 30 minutes.
2. Utilise cette relation pour calculer en 150 km/h la vitesse d'une automobile qui parcourt, à vitesse constante sur l'autoroute, 150 km en 1 h 30 minutes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22Durée du parcours de la lumière du Soleil.
La valeur de la vitesse de la lumière est environ égale à 300 000 km/s. Le Soleil est à une distance approximative de 150 millions de kilomètres de la Terre.
1. Calcule la durée nécessaire à la lumière du Soleil pour nous parvenir.
1. Calcule la durée nécessaire à la lumière du Soleil pour nous parvenir.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Une notion, trois exercices Différenciation
Compétence : Produire et transformer des tableaux ou des documents graphiques.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23-ALe sonar. Le sonar et l'exploitation marine.
Le sonar est un appareil qui utilise un son inaudible par l'oreille humaine. Ce son est réfléchi par les obstacles (par exemple le fond marin) et revient vers l'appareil (écho). La durée entre l'envoi et la réception permet de déduire la distance à laquelle se trouve l'obstacle. Dans un bateau d'exploration scientifique, un écho sur le fond marin est entendu 1,20 s après l'émission du signal. La vitesse des ondes sonores dans l'eau de mer est de 1 500 m/s.
On cherche à déterminer la profondeur du fond marin par rapport au bateau.
1. Calcule la durée nécessaire à la lumière du Soleil pour nous parvenir.
2. Réalise un schéma simple de la situation et trace sur ce schéma le trajet des ondes sonores.
3. Rappelle la relation entre la vitesse v, la durée t et la distance d.
4. Déduis-en l'expression de la distance d en fonction de la vitesse v et de la durée t.
5. Indique, d'après ton schéma, combien de fois l'onde sonore parcourt la distance entre le bateau et le fond marin.
6. Déduis-en si la distance est deux fois trop grande ou deux fois trop petite.
7. Calcule en mètres (valeur arrondie à l'unité) la profondeur du fond marin par rapport au bateau.
On cherche à déterminer la profondeur du fond marin par rapport au bateau.
1. Calcule la durée nécessaire à la lumière du Soleil pour nous parvenir.
2. Réalise un schéma simple de la situation et trace sur ce schéma le trajet des ondes sonores.
3. Rappelle la relation entre la vitesse v, la durée t et la distance d.
4. Déduis-en l'expression de la distance d en fonction de la vitesse v et de la durée t.
5. Indique, d'après ton schéma, combien de fois l'onde sonore parcourt la distance entre le bateau et le fond marin.
6. Déduis-en si la distance est deux fois trop grande ou deux fois trop petite.
7. Calcule en mètres (valeur arrondie à l'unité) la profondeur du fond marin par rapport au bateau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23-BLe sonar. Le sonar militaire.
Le sonar est un appareil qui utilise un son inaudible par l'oreille humaine. Ce son est réfléchi par les obstacles (par exemple un sous-marin) et revient vers l'appareil (écho). La durée entre l'envoi et la réception permet de déduire la distance à laquelle se trouve l'obstacle. Dans un bateau militaire, un écho sur un sous-marin est entendu 0,40 s après l'émission du signal. La vitesse des ondes sonores dans l'eau de mer est de 1 500 m/s.
On cherche à déterminer la distance du sous-marin par rapport au bateau.
1. Réalise un schéma simple de la situation et trace sur ce schéma le trajet des ondes sonores.
2. Donne l'expression mathématique de la distance d en fonction de la vitesse v et la durée t.
3. Indique, d'après ton schéma, si le résultat que te donnera cette formule sera deux fois trop grand ou deux fois trop petit (d'après le trajet des ondes sonores).
4. Calcule en mètres (valeur arrondie à l'unité) la distance du sous-marin par rapport au bateau.
On cherche à déterminer la distance du sous-marin par rapport au bateau.
1. Réalise un schéma simple de la situation et trace sur ce schéma le trajet des ondes sonores.
2. Donne l'expression mathématique de la distance d en fonction de la vitesse v et la durée t.
3. Indique, d'après ton schéma, si le résultat que te donnera cette formule sera deux fois trop grand ou deux fois trop petit (d'après le trajet des ondes sonores).
4. Calcule en mètres (valeur arrondie à l'unité) la distance du sous-marin par rapport au bateau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23-CLe sonar. Le sonar et la pêche.
Le sonar est un appareil qui utilise un son inaudible par l'oreille humaine. Ce son est réfléchi par les obstacles (un banc de poissons par exemple) et revient vers l'appareil (écho). La durée entre l'envoi et la réception permet de déduire la distance à laquelle se trouve l'obstacle. Dans un bateau de pêche, un écho sur un banc de poissons est entendu 0,10 s après l'émission du signal. La vitesse des ondes sonores dans l'eau de mer est de 1 500 m/s.
On cherche à déterminer la profondeur du banc de poissons par rapport au bateau.
1. Réalise un schéma simple de la situation et trace sur ce schéma le trajet des ondes sonores.
2. Calcule en mètres (valeur arrondie à l'unité) la profondeur du banc de poissons par rapport au bateau.
On cherche à déterminer la profondeur du banc de poissons par rapport au bateau.
1. Réalise un schéma simple de la situation et trace sur ce schéma le trajet des ondes sonores.
2. Calcule en mètres (valeur arrondie à l'unité) la profondeur du banc de poissons par rapport au bateau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Chute libre.
Compétence
Utiliser l'outil informatique pour acquérir et traiter des données, simuler des phénomènes.
On réalise la chronophotographie d'une chute libre. L'intervalle de temps entre deux positions (c'est-à-dire entre deux prises de vue) est de 0,1 s.
1. Le tableau suivant donne un extrait des résultats obtenus.
| Distance (m) | Durée (s) | Écart (m) | Vitesse (m/s) |
| 0,56 | 0,7 | ||
| 0,69 | 0,8 | 0,69 - 0,56 = 0,13 | 0,13 / 0,1 = 1,3 |
| 0,84 | 0,9 | ||
| 1,01 | 1 | ||
| 1,20 | 1,1 |
2. Pour calculer l'écart, c'est-à-dire la distance parcourue pendant chaque intervalle de 0,1 s, on fait la différence entre une position de la colonne 1 et la précédente (voir exemple donné dans le tableau pour l'écart entre les deux premières lignes). Recopie les valeurs dans un tableur, puis, à l'aide d'une formule, complète la colonne des écarts (troisième colonne du tableau).
3. Pour calculer la vitesse, on divise la distance parcourue par la durée du parcours. C'est donc le résultat de la troisième colonne divisé par 0,1 (durée de l'intervalle). Complète la quatrième colonne du tableau.
4. Le mouvement est-il rectiligne ? Justifie ta réponse.
5. Le mouvement est-il uniforme ? Justifie ta réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Excès de vitesse.
À l'aide d'un radar, une automobile en excès de vitesse est flashée sur un tronçon d'autoroute. L'ayant arrêtée au péage, les gendarmes prennent le ticket du conducteur. Il a pris le ticket à 15 h 12, il est 15 h 41.
1. Calcule la durée du parcours.
2. La distance parcourue est de 94 kilomètres. Calcule la vitesse moyenne sur ce parcours.
3. La vitesse calculée à la question 2 et la vitesse relevée par le radar sont-elles de même nature ? Justifie la réponse.
4. La vitesse limite sur autoroute est de 130 km/h. Fais des recherches et détermine ce que risque l'automobiliste.
1. Calcule la durée du parcours.
2. La distance parcourue est de 94 kilomètres. Calcule la vitesse moyenne sur ce parcours.
3. La vitesse calculée à la question 2 et la vitesse relevée par le radar sont-elles de même nature ? Justifie la réponse.
4. La vitesse limite sur autoroute est de 130 km/h. Fais des recherches et détermine ce que risque l'automobiliste.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Record de vitesse à la voile.
Il existe deux catégories de records de vitesse à la voile : sur 500 m et sur 1 mille marin (1 852 m). Le 24 novembre 2012, l'Australien Paul Larsen établit un nouveau record du monde de vitesse sur 500 m à 65,45 nœuds de moyenne, avec une pointe à plus de 67 nœuds. Le nœud est l'unité utilisée pour déterminer la vitesse des bateaux et des avions. 1 nœud = 1 852 m/h.
1. Calcule en m/s et en km/h (valeurs arrondies au centième) la valeur de ce record du monde.
1. Calcule en m/s et en km/h (valeurs arrondies au centième) la valeur de ce record du monde.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Séisme.
Compétence
Lire et comprendre des documents scientifiques pour en extraire des informations.
Plusieurs types d'ondes sismiques peuvent être produites. L'une d'elles, l'onde de Love, circule en surface à la vitesse approximative de 4 km/s. C'est elle qui est responsable de l'ébranlement des fondations des immeubles. En France, de petits séismes se produisent régulièrement, par exemple dans la chaine des Pyrénées. À 19 km de Lourdes, le 16 août 2016 à 19 h 34, un séisme de magnitude 2,3 a été détecté. En dessous de 4, on parle de séisme mineur, voire de microséisme. Ils ne sont pas ressentis par la population.
1. En combien de temps l'onde de Love de ce seisme a-t-elle atteint la ville de Lourdes ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Satellite géostationnaire.
Compétence
Présenter mon résultat avec l'unité adaptée.
Un satellite est dit géostationnaire s'il reste toujours à la verticale du même point situé sur le sol. Cela signifie que sa vitesse de rotation est constante et égale à celle de la Terre : il fait un tour en 24 h.
1. Le mouvement d'un satellite géostationnaire est-il rectiligne ?
2. Est-il uniforme ?
3. Sachant que ce satellite se situe à environ 39 000 km du centre de la Terre, calcule en km la circonférence de sa trajectoire (rappel : la circonférence d'un cercle est égale à 2 × π × rayon). Arrondis la valeur à l'unité.
4. Le satellite parcourt cette distance en 24 h. Calcule sa vitesse en km/h (arrondie à l'unité).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Grand Prix d'Espagne.
Au Grand Prix automobile d'Espagne 2016, sur le circuit de Barcelona-Catalunya, la longueur de la piste est de 4,665 km. La course comprend 66 tours. Max Verstappen est arrivé premier en 1 h 41 min et 40,017 s. Le suivant, Kimi Räikkönen, est arrivé 0,616 s après lui.
1. Calcule la distance totale parcourue lors du Grand Prix.
2. Calcule la durée de la course de Kimi Räikkönen.
3. Calcule en km/h et en m/s la vitesse moyenne de Max Verstappen et celle de Kimi Räikkönen (vitesses arrondies au dixième près). Que constates-tu ?
4. En supposant que les vitesses des deux pilotes étaient de 260 km/h à l'arrivée, calcule la distance qui les sépare quand Max Verstappen a franchi la ligne d'arrivée (arrondie à l'unité).
1. Calcule la distance totale parcourue lors du Grand Prix.
2. Calcule la durée de la course de Kimi Räikkönen.
3. Calcule en km/h et en m/s la vitesse moyenne de Max Verstappen et celle de Kimi Räikkönen (vitesses arrondies au dixième près). Que constates-tu ?
4. En supposant que les vitesses des deux pilotes étaient de 260 km/h à l'arrivée, calcule la distance qui les sépare quand Max Verstappen a franchi la ligne d'arrivée (arrondie à l'unité).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Vitesse du son.
La vitesse du son dans l'air varie selon la température, mais aussi en fonction de la pression et de diverses modifications du milieu comme sa composition.
1. Calcule en km/h la vitesse du son à -10 °C et à 25 °C.
2. Déduis-en la différence de distance parcourue en une heure à ces deux températures.
| Température (en °C) | Vitesse (en m/s) |
| -10 | 325,2 |
| -5 | 328,3 |
| 0 | 331,3 |
| 5 | 334,3 |
| 10 | 337,4 |
| 15 | 340,4 |
| 20 | 343,4 |
| 25 | 346,5 |
1. Calcule en km/h la vitesse du son à -10 °C et à 25 °C.
2. Déduis-en la différence de distance parcourue en une heure à ces deux températures.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Distance Terre-Lune.
Pour mesurer la distance Terre-Lune, une des techniques consiste à envoyer un faisceau laser sur un des réflecteurs qui a été posé sur la Lune et à mesurer la durée de l'aller-retour entre l'émission et la réflexion. Lors d'une expérience, cette durée est de 2,559 s La valeur connue actuellement de la vitesse de la lumière est de 299 792,45898 km/s.
1. Calcule la distance entre la Terre et la Lune le jour de la mesure (arrondie au km). N'oublie pas de tenir compte du fait que la lumière parcourt deux fois le trajet.
1. Calcule la distance entre la Terre et la Lune le jour de la mesure (arrondie au km). N'oublie pas de tenir compte du fait que la lumière parcourt deux fois le trajet.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32Tour de France cycliste.
Christopher Froome a remporté le tour de France 2016. Il a parcouru les 3 519 km en 89 h 04 min et 48 s.
Le dernier classé, Sam Bennett, est resté 5 h 17 min et 14 s de plus sur son vélo.
1. Calcule la vitesse moyenne de Christopher Froome.
2. Calcule la vitesse moyenne de Sam Bennett.
Le dernier classé, Sam Bennett, est resté 5 h 17 min et 14 s de plus sur son vélo.
1. Calcule la vitesse moyenne de Christopher Froome.
2. Calcule la vitesse moyenne de Sam Bennett.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Voyage en train.
Sur le site de la SNCF, Anna recherche les horaires du prochain train PARIS-NÎMES. Elle obtient le résultat suivant :
19 h 15 : PARIS-GARE DE LYON
22 h 03 : NÎMES
1. Calcule la durée du trajet en heures et en minutes.
2. Convertis cette durée en heures.
3. La distance entre les deux villes est de 715 kilomètres. Calcule la vitesse en km/h et en m/s.
19 h 15 : PARIS-GARE DE LYON
22 h 03 : NÎMES
1. Calcule la durée du trajet en heures et en minutes.
2. Convertis cette durée en heures.
3. La distance entre les deux villes est de 715 kilomètres. Calcule la vitesse en km/h et en m/s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34Record du monde de nage libre.
Le 12 aout 2016, la nageuse Katie Ledecky bat le record du monde sur 800 m nage libre aux jeux de Rio, 2016, en 8 min et 4,79 s.
1. Calcule sa vitesse en km/h (arrondie au centième).
1. Calcule sa vitesse en km/h (arrondie au centième).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je résous un problème
Compétence : Lire et comprendre des documents scientifiques pour en extraire des informations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Détermine le nombre d'années nécessaires à Pioneer 10 pour atteindre Aldebaran. Commente ton résultat.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Aldebaran, dans la constellation du Taureau.


La sonde se dirige actuellement vers l'étoile Aldebaran, la plus brillante sur cette image, située à environ 65 années-lumière du Soleil, ce qui est proche à l'échelle de la galaxie, large de 100 000 années lumière. On rappelle qu'une année-lumière est la distance parcourue par la lumière en un an, sa vitesse étant de l'ordre de 300 000 km/s.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2La sonde Pioneer 10.


La sonde Pioneer 10 a été lancée le 3 mars 1972 par la NASA. Après avoir survolé Mars, la ceinture d'astéroïde, puis Jupiter, elle a dépassé les orbites de Neptune et Pluton pour quitter le système solaire. Le dernier contact avec la sonde a eu lieu le 22 janvier 2013.
Sa vitesse moyenne est de l'ordre de 52 000 km/h. C'est le plus rapide des objets construits par l'Homme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Distance des éclairs.
Lorsqu'un éclair apparait dans le ciel, sa lumière nous parvient presque instantanément. Quelques secondes plus tard, le son nous arrive. Pour connaître la distance approximative, en kilomètres, entre nous et l'impact de la foudre, on dit qu'il suffit de diviser le temps entre l'éclair et le son par 3. Par exemple, si le bruit de l'éclair arrive au bout de 6 secondes, alors l'éclair s'est produit à \dfrac{6}{3} = 2 kilomètres. Nous allons essayer de vérifier cela.
1. On suppose que l'impact a eu lieu à 10 km. La vitesse de la lumière est de l'ordre de 300 000 km/s, celle du son de 330 m/s. Calcule pour la lumière le temps (en s) mis pour parcourir ces 10 km. Arrondis la valeur au millionième.Calcule, pour le son, le temps (en s) mis pour parcourir ces 10 km. Arrondis la valeur au dixième.
2. En comparant ces deux durées, que penses-tu de l'hypothèse disant que la lumière arrive presque instantanément par rapport au son ?
3. Divise maintenant par 3 le temps trouvé pour le son et compare le résultat avec la distance choisie (10 km).
4. L'hypothèse donnée dans le texte pour le calcul est-elle bonne ?
5. Lors d'un orage, un premier éclair te parvient 7 secondes après la foudre. En utilisant la technique que nous venons de vérifier, calcule la distance approximative en kilomètres (arrondie au dixième).
6. Trois minutes plus tard, ce temps n'est plus que de 4 secondes. Calcule la nouvelle distance (arrondie au dixième). N'est-il pas temps de débrancher les appareils électriques sensibles ?
1. On suppose que l'impact a eu lieu à 10 km. La vitesse de la lumière est de l'ordre de 300 000 km/s, celle du son de 330 m/s. Calcule pour la lumière le temps (en s) mis pour parcourir ces 10 km. Arrondis la valeur au millionième.Calcule, pour le son, le temps (en s) mis pour parcourir ces 10 km. Arrondis la valeur au dixième.
2. En comparant ces deux durées, que penses-tu de l'hypothèse disant que la lumière arrive presque instantanément par rapport au son ?
3. Divise maintenant par 3 le temps trouvé pour le son et compare le résultat avec la distance choisie (10 km).
4. L'hypothèse donnée dans le texte pour le calcul est-elle bonne ?
5. Lors d'un orage, un premier éclair te parvient 7 secondes après la foudre. En utilisant la technique que nous venons de vérifier, calcule la distance approximative en kilomètres (arrondie au dixième).
6. Trois minutes plus tard, ce temps n'est plus que de 4 secondes. Calcule la nouvelle distance (arrondie au dixième). N'est-il pas temps de débrancher les appareils électriques sensibles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36Unités du système international (SI).
1. Quelles sont les unités internationales de distance, de temps et de vitesse ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37Conversions de vitesses.
Effectue les conversions suivantes :
1. 80 km/h = m/s.
2. 25 m/s = km/h.
3. 43 cm/s = m/s.
1. 80 km/h =
2. 25 m/s =
3. 43 cm/s =
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38Course.
Un coureur parcourt la distance de 60 m à la vitesse de 8,3 m/s.
1. Calcule le temps mis pour faire les 60 m (arrondi au centième).
1. Calcule le temps mis pour faire les 60 m (arrondi au centième).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39Mouvement rectiligne et uniforme.
1. Rappelle en une phrase ce qu'est un mouvement rectiligne et uniforme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours de compétences
Compétence : Conclure, valider ou non l'hypothèse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tchat entre ados sur la même route, dans des voitures parties à des heures différentes.
1. La vitesse du bouchon est-elle bien celle qu'indique Maxime ?
- Maxime 10 h 43 : Galère au kilomètre 200 : on entre dans les bouchons ! :-/
- Leila 10 h 44 : Départ aux aurores = loose totale. Je vais te rattraper ^^ !
- Maxime 10 h 45 : Un bouchon remonte le flux des voitures à 30 km/h. Tu seras coincée avant !
- Leila 11 h 13 : T'avais raison. Kilomètre 210 ; Galère 2 : c'est mon tour ! On entre dans les bouchons :-/
1. La vitesse du bouchon est-elle bien celle qu'indique Maxime ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 1
J'identifie l'hypothèse à évaluer.
Coup de pouce
D'après Maxime, quelle est la vitesse du bouchon ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 2
Je rappelle les résultats en lien avec l'hypothèse.
Coup de pouce
Relève les informations importantes pour résoudre le problème.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 3
Je valide ou non l'hypothèse, après avoir constaté que les résultats sont en accord ou non avec elle.
Coup de pouce
Divise la distance qui sépare les points d'arrivée dans le bouchon par la durée écoulée entre les arrivées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 4
Je valide ou non l'hypothèse, en précisant comment elle s'accorde ou pas avec les résultats.
Coup de pouce
D'après Maxime, à quelle heure Leila aurait-elle dû entrer dans le bouchon ? Que conclure ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

