Chapitre 2
J'apprends
Nombres relatifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ANombres relatifs et repérage
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Définitions
Repérage
Sur une droite graduée orientée, on représente les nombres positifs à droite de zéro et négatifs à gauche de zéro.


Exercices n° p. 38
- Le nombre zéro est à la fois de signe positif et négatif.
- Chaque point sur la droite graduée est associé à un nombre appelé « abscisse » de ce point.
Exemple :

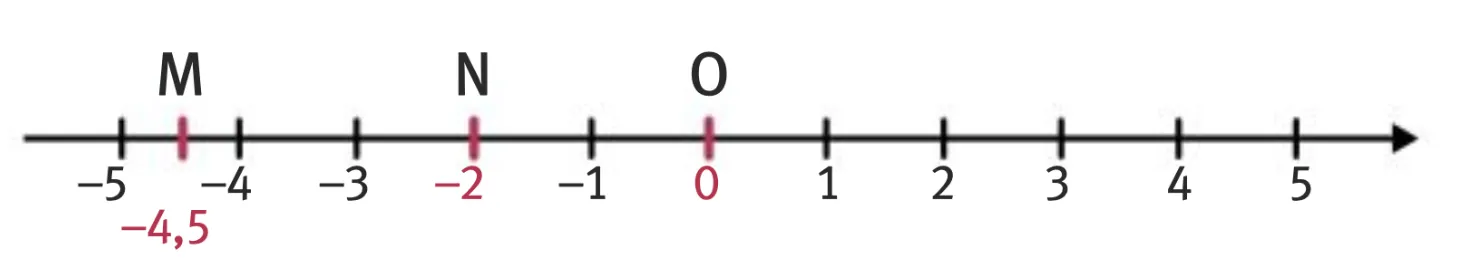
- L'abscisse du point M est -4\text{,}5, il est à gauche de 0 donc -4\text{,}5~\text{\textless}~0.
- Le point N d'abscisse -2 est à droite de M donc -2 > -4\text{,}5.
Définition
On écrit un nombre relatif avec un signe (+ : signe positif ; – : signe négatif) et un nombre appelé « distance à zéro ». Quand le signe nʼest pas mentionné, il sʼagit du signe « + ».
Signe négatif \to \undergroup {-}~\undergroup {5,2} \gets Distance à zero
Absence de signe, donc positif \to \undergroup {}~\undergroup {3} \gets Distance à zero
Signe négatif \to \undergroup {-}~\undergroup {5,2} \gets Distance à zero
Absence de signe, donc positif \to \undergroup {}~\undergroup {3} \gets Distance à zero
Exercices n° p. 38
Exemple :
-7\text{,}8 est un nombre relatif :
- il est négatif (signe « − ») ;
- sa distance à zéro est 7\text{,}8.
- -\dfrac{1}{3} est également un nombre négatif ; sa distance à zéro est \dfrac{1}{3}.
Définition
Lʼopposé dʼun nombre est le nombre de signe contraire qui est à la même distance de zéro.
Exercices n° p. 38 et 41
Exemple :

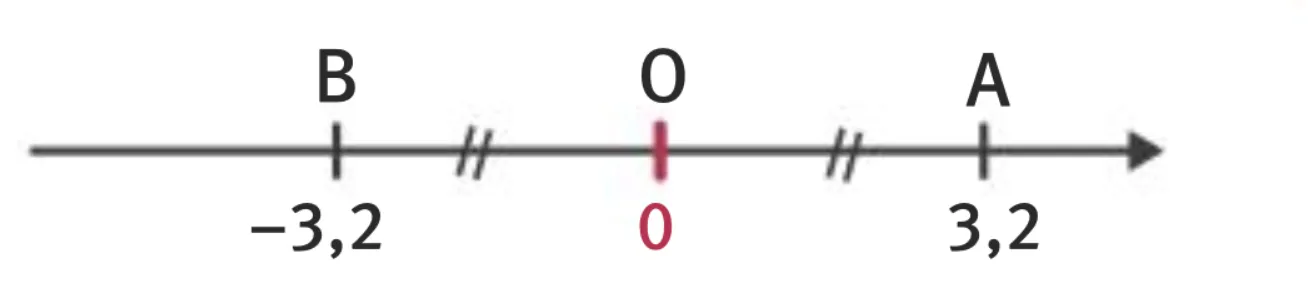
-3\text{,}2 est lʼopposé de 3\text{,}2.
3\text{,}2 est lʼopposé de -3\text{,}2.
Remarques :
- Lʼopposé de zéro est zéro.
- Sur une droite graduée, deux points dʼabscisses opposées sont symétriques par rapport à lʼorigine du repère.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Se repérer avec les nombres relatifs
Repérage
Pour construire un repère orthonormé du plan :
- On trace deux axes perpendiculaires :
- Un axe (Ox), souvent horizontal, orienté vers la droite. Cʼest lʼaxe des abscisses.
- Un axe (Oy), souvent vertical, orienté vers le haut. Cʼest lʼaxe des ordonnées.
- Lʼintersection de ces deux axes est lʼorigine du repère, quʼon appelle généralement O.
- On définit une unité. On place un point I sur lʼaxe des abscisses et un point J sur lʼaxe des ordonnées afin de définir lʼunité de longueur OI = OJ = 1. Ce repère est noté le repère (O, I, J).


Exercices n° p. 38 et 39
Le point A(3 ; -2) a pour abscisse 3 et pour ordonnée -2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Comparer des nombres relatifs
Définition
Comparer deux nombres, cʼest dire si lʼun est strictement inférieur ou supérieur à lʼautre, ou sʼils sont égaux.
Exercices n° p. 38 et 39
Méthode
Ces règles de comparaison sont toujours vraies :
- Les nombres positifs sont plus grands que les nombres négatifs.
- Parmi les nombres positifs, le plus grand est celui qui est à la plus grande distance de zéro.
- Parmi les nombres négatifs, le plus grand est celui qui est à la plus petite distance de zéro.
- De manière générale, sur une droite graduée orientée vers la droite, le nombre le plus petit est toujours celui qui est le plus à gauche, et le plus grand le plus à droite.
Exercices n° p. 39
Pour comparer ces nombres, on lit de gauche à droite sur la droite orientée.
On a donc
-2~\text{,}5~\text{\textless}-1~\text{\textless}~0~\text{\textless}~1~\text{\textless}~3\text{,}2.
-2~\text{,}5~\text{\textless}-1~\text{\textless}~0~\text{\textless}~1~\text{\textless}~3\text{,}2.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BAddition et soustraction
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Définitions
Méthode
Pour additionner deux nombres relatifs, on procède ainsi :
- si les deux nombres sont de même signe, alors on conserve le signe commun et on additionne les distances à zéro ;
- si les deux nombres sont de signes opposés, alors on prend le signe de celui qui a la plus grande distance à zéro et on soustrait les distances à zéro.
Exercices n° p. 39
et 41
J'applique
Consigne :
Additionnez (-3) et (-8).
Correction :
Additionnez (-3) et (-8).
Correction :
- Le signe commun est « - », donc la somme sera un nombre négatif.
- 3 + 8 = 11, donc la distance à zéro sera égale à 11.
- On place devant la distance à zéro obtenue le signe déterminé précédemment.
Donc (-8) + (-3) = (-11).
Consigne :
Effectuez lʼaddition de 3 et (-7).
Correction :
Effectuez lʼaddition de 3 et (-7).
Correction :
- Les deux distances à zéro sont 3 et 7.
Le nombre qui est à la plus grande distance à zéro est −7, dont le signe est « − ».
La somme obtenue sera donc un nombre négatif. - 7 - 3 = 4, donc la distance à zéro sera égale à 4.
- On place devant la distance à zéro obtenue le signe déterminé précédemment.
Donc 3 + (-7) = -4.
Remarque : Lʼaddition dʼun nombre et de son opposé donne toujours 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Soustraction
Méthode
Soustraire un nombre relatif, cʼest additionner son opposé.
a - (-b) = a + (+b) = a + b et a - b = a - (+b) = a + (-b).
a - (-b) = a + (+b) = a + b et a - b = a - (+b) = a + (-b).
Exercices n° p. 39 et 41
J'applique
Consigne :Faites la soustraction de (-2) par (-7).
Correction :
- On veut calculer -2 - (-7).
- Lʼopposé de (-7) est +7.
Donc -2 - (-7) = -2 + (+7)
= -2 + 7
= 7 - 2
= 5
Remarques :
- Lʼaddition est commutative, cʼest-à-dire que lʼon peut additionner dans lʼordre que lʼon veut :
a + b = b + a.
(-3) + 5 = 5 + (-3) - La soustraction nʼest pas commutative :
a - b \neq b - a.
7 - 3 = 4
3 - 7 = -4
7 - 3 \neq 3 - 7 - Enlever les signes « − », « + », et les parenthèses inutiles dʼune expression, cʼest simplifier son écriture.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C Multiplication et division
J'approfondis
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
La règle des signes : le signe dʼun produit de nombres relatifs dépend du nombre de facteurs négatifs.
- Si le nombre de facteurs négatifs est pair, alors le produit est positif.
- Si le nombre de facteurs négatifs est impair, alors le produit est négatif.
Exercices n° p. 41 et 43
J'applique
Consigne :Quel est le résultat de la multiplication suivante ?
(-1) \times (-4) \times 2 \times (-0 \text{,} 5) \times (-7)
Correction :
Il y a quatre signes « − ». Puisquʼil y a un nombre pair de nombres négatifs, le résultat est donc positif :
(-1) \times (-4) \times 2 \times (-0 \text{,} 5) \times (-7) = 1 \times 4 \times 2 \times 0 \text{,} 5 \times 7 = 28
Aide
Le produit de deux nombres relatifs de même signe est positif.
Le produit de deux nombres relatifs de signes contraires est négatif.
Le produit de deux nombres relatifs de signes contraires est négatif.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

