	Pour s'échauffer	Pour commencer	Pour s'entraîner
Savoir exploiter la loi de Beer-Lambert :	9	20	30
Savoir exploiter la loi de Kohlrausch :		15	25
Savoir utiliser une courbe d'étalonnage :		17 21	28
Savoir utiliser un spectre UV ou IR pour identifier une espèce chimique :		18	34

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour s'échauffer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Conductance et résistance

Déterminer la résistance d'une portion de solution dont la conductance vaut G = 280 mS.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Mesure de conductance

Schématiser le montage expérimental permettant la mesure de la conductance d'une solution sans utiliser un conductimètre.

Cliquez pour accéder à une zone de dessin

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Dilution

Décrire le protocole permettant d'obtenir 50{,}0 mL d'une solution fille à partir d'une solution mère que l'on dilue au vingtième.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Loi de Kohlrausch

Rappeler la loi de Kohlrausch en précisant les unités utilisées.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Loi de Beer-Lambert

Rappeler la loi de Beer-Lambert en précisant les unités.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
Nombre d'onde

Sur un spectre infrarouge, rappeler à quoi correspond le nombre d'onde \bar{\nu}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
Absorption de lumière

Déterminer la couleur de la solution dont le spectre est présenté ci-dessous.

Cercle chromatique
en rabat de fin.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour commencer

Conductance et conductivité

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
Lien entre conductance et conductivité

✔ REA : Appliquer une formule

On mesure la conductance d'une solution ionique entre deux plaques, dont la surface est S = 2{,}0 cm², distantes de l = 5{,}0 mm. On obtient G = 3{,}41 mS.

1. Exprimer la conductivité σ de la solution en fonction de G, S, l.

2. Calculer cette conductivité.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
Mesure de la conductance d'une solution

✔ REA : Appliquer une formule

Entre deux plaques métalliques plongées dans une solution, on mesure U = 2{,}00 V et I = 56 mA.

Déterminer la conductance G de cette portion de solution.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
Cellule de conductimétrie

✔ APP : Extraire l'information utile

On plonge une cellule de conductimétrie dans une solution pour mesurer sa conductivité \sigma. Les caractéristiques de la cellule de mesure du conductimètre sont présentées dans les données ci‑dessous.

Déterminer la valeur de la conductivité affichée par le conductimètre lors de la mesure.

Données

Surface de la cellule de mesure : S = 0{,}16 cm²
Distance entre les plaques : l = 0{,}40 cm
Résolution de l'appareil : arrondi au millième pour 2 mS·cm^-1 et au centième pour 20 mS·cm^-1
Tension mesurée lors de la mesure : U = 2{,}00 V
Intensité mesurée lors de la mesure : I = 6{,}3 mA

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Loi de Kohlrausch

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Détermination d'une conductivité

✔ REA : Appliquer une formule

On dispose d'une solution S₁ d'hydroxyde de sodium \text{(Na}^+\text{(aq)} ; \text{HO}^-\text{(aq)}), de concentration c_1 = 0{,}200 mol·L^-1 en soluté apporté.

Calculer la conductivité \sigma de cette solution.

Données

Conductivités molaires ioniques à 25 °C :
\lambda\left(\mathrm{Na}^{+}\right)=5{,}01 \times 10^{-3} S·m²·mol^-1 et
\lambda\left(\mathrm{HO}^{-}\right)=19{,}8 \times 10^{-3} S·m²·mol^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
Conversions d'unité

✔ REA : Appliquer une formule

1. Exprimer en (mol·L^-1) les concentrations suivantes :

a. c_1 = 5{,}0 mol·m^-3.

b. c_2 = 0{,}050 mol·m^-3.

2. Exprimer en (mol·m^-3) les concentrations suivantes :

a. c_3 = 5{,}0 mol·L^-1.

b. c_4 = 5{,}0 mmol·L^-1.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
Dosage par étalonnage

✔ RAI/ANA : Utiliser et interpréter des documents

Pour déterminer la concentration d'une solution d'iodure de potassium (\text{K}^+ \text{(aq)} ; \text{I}^-\text{(aq)}), on procède à un dosage par étalonnage en mesurant la conductivité \sigma de plusieurs solutions d'iodure de potassium de concentration connue.

Concentration c (mmol·L^-1)	1{,}0	2{,}0	3{,}0	4{,}0	5{,}0	6{,}0
Conductivité \sigma (mS·cm^-1)	3{,}43	6{,}85	10{,}3	13{,}7	17{,}2	20{,}6

1. Tracer la courbe \sigma = f(c) à l'aide d'un tableur ou sur la calculatrice.

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

On plonge la même cellule de mesure dans la solution à analyser. La conductivité mesurée est \sigma = 16{,}3 mS·cm^-1.

2. Déterminer la concentration de la solution analysée.

Doc.
Boîte de comprimés d'iodure de potassium

Plaquette comprimés iodure potassium 65mg, protection thyroïde accident nucléaire. Usage sur recommandation autorités.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Analyse spectrale

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
Colorant alimentaire

✔ VAL : Analyser des résultats

On présente ci-dessous le spectre UV-visible d'une espèce moléculaire utilisée comme colorant alimentaire.

Photo de deux flacons de colorant alimentaire, un bleu et un rouge, prêts à l'emploi.

1. À partir du spectre fourni, déterminer de quelle couleur l'œil humain perçoit cette solution colorée.

Cercle chromatique
en rabat de fin.

2. Proposer une longueur d'onde pertinente pour réaliser un dosage par étalonnage de ce colorant en précisant pourquoi.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Spectre infrarouge

✔ APP : Extraire l'information utile

1. Nommer les molécules dont on a représenté les modèles moléculaires.

Fiche méthode 14

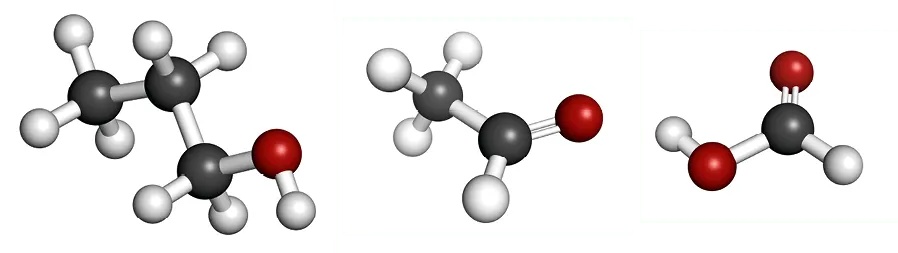
Modèles moléculaires 3D du propan-1-ol, du propanal et de l'acide propanoïque.

2. Le spectre infrarouge représenté ci-dessous est celui d'une de ces molécules. Préciser laquelle en analysant la présence ou non de bandes caractéristiques.

Fiche méthode 16
.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Loi de Beer-Lambert

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
Permanganate de potassium

✔ RAI/ANA : Justifier un protocole

On dispose d'une solution de permanganate de potassium, de concentration approximativement égale à 2 mmol·L^-1. On souhaite connaître plus précisément cette concentration. On procède pour cela à un dosage par étalonnage à la longueur d'onde \sigma = 540 nm.

1. Déterminer l'absorbance théorique de cette solution.

2. Expliquer pourquoi on ne pourra pas déterminer avec fiabilité la concentration de la solution.

3. Proposer une solution pour pallier ce problème.

Données

Longueur de la cuve utilisée : l = 1 cm
Gamme de mesure du spectrophotomètre : -0,97\lt A \lt 2,5
Coefficient d'absorption molaire du permanganate de potassium à la longueur d'onde utilisée : \varepsilon_{540 \mathrm{nm}}=2,2 \times 10^{3} L·mol^-1·cm^-1

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21
Diiode

✔ RAI/ANA : Utiliser et interpréter des documents

Le diiode \text{I}_2\text{(aq)} est une espèce chimique peu soluble dans l'eau. On procède au dosage par étalonnage d'une solution de diiode par spectrophotométrie.

Concentration \boldsymbol{c} (μmol·L^-1)	50	250	750	1 000
Absorbance A	0{,}041	0{,}220	0{,}703	0{,}872

1. Les mesures ont été obtenues à \lambda = 470 nm, longueur d'onde pour laquelle la molécule de diiode présente une absorbance maximale. En déduire la couleur de la solution de diiode.

Cercle chromatique
en rabat de fin.

2. À l'aide d'un tableur ou de la calculatrice, déterminer l'équation de la droite représentative de A = f(c), modélisant la série de données.

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

3. La solution de diiode analysée présente une absorbance A = 0,514. Déterminer sa concentration en quantité de matière.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Une notion, trois exercices
Différenciation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
Incertitude d'un appareil de mesure

✔ VAL : Évaluer les incertitudes

Voici ce qu'annonce le constructeur d'un conductimètre sur la notice de son appareil :

gamme : 0-20 mS·cm^-1 ;
résolution : d = 0,01 mS·cm^-1.

L'incertitude liée à la résolution de l'appareil se calcule selon la relation :

u(\sigma)=\frac{d}{2 \sqrt{3}}

1. Préciser la signification des deux indications fournies.

2. Calculer l'incertitude u(\sigma) sur la mesure.

3. L'appareil affiche \sigma = 2{,}73 mS·cm^-1. Donner un encadrement de la conductivité mesurée.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Incertitudes de mesure et calcul

✔ VAL : Évaluer les incertitudes

Pour déterminer la conductance G d'une portion de solution, on dispose de sa tension U et de l'intensité I du courant qui la traverse, précisées dans les données.

1. Déterminer les incertitudes u(U) et u(I) sur les valeurs de la tension et de l'intensité.

2. Calculer l'incertitude type composée qui en résulte pour la valeur de la conductance sachant que :

\frac{u(G)}{G}=\sqrt{\left(\frac{u(U)}{U}\right)^{2}+\left(\frac{u(I)}{I}\right)^{2}}

3. En déduire une valeur encadrée de la conductance G de la solution.

Données

Tension mesurée : U = 2{,}00 \text{V}
Intensité mesurée : I = 0{,}045 \text{A}
Incertitude des multimètres utilisés : ± \ 0,09 %

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
Incertitude sur une série de mesures

✔ VAL : Évaluer les incertitudes

Pour déterminer la conductivité d'une solution de manière précise, on décide de réaliser trente fois la mesure avec le même matériel, utilisé par une même personne.

Conductivité \boldsymbol{\sigma} (mS·cm^-1)	65{,}42	65{,}43	65{,}44	65{,}45
Nombre de mesures \boldsymbol{n}	4	9	12	5

1. Déterminer la valeur moyenne de la conductivité.

2. À l'aide de la calculatrice ou d'un tableur, déterminer l'incertitude correspondant au rapport entre l'écarttype de la série de mesures et la racine carrée du nombre total de mesures.

3. Expliquer quel est l'intérêt de ne changer ni de matériel ni d'expérimentateur au cours de la série de mesures.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Conductivité de l'eau

✔ REA : appliquer une formule

Calculer la conductivité de l'eau distillée à pH = 7,0 et à 25°C.

Données

Relation entre les concentrations dans l'eau à 25 °C : \frac{\left[\mathrm{HO}^{-}\right] \cdot\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{c^{2}}=K_{e}

Conductivités molaires ioniques à 25°C : \lambda\left(\mathrm{HO}^{-}\right)=19{,}8 mS·m²·mol^-1 et \lambda\left(\mathrm{H}_{3} \mathrm{O}^{+}\right)=35{,}0 mS·m²·mol^-1
Produit ionique de l'eau : K_{e}=10^{14}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Coefficient d'absorption molaire

Le bleu patenté est une molécule utilisée comme colorant alimentaire, ayant une forte absorption autour de 630 nm. On mesure l'absorption à travers une cuve de largeur 1,0 cm d'une solution aqueuse de bleu patenté de concentration 5,0 × 10-6 mol·L^-1 pour une longueur d'onde de 630 nm. On trouve 0,49.

1. Justifier que cette molécule est bleue.

2. Pourquoi faut‑il faire un blanc avant la mesure de l'absorbance ? Que faut‑il mettre dans la cuve pour faire le blanc ?

3. Calculer le coefficient d'absorption molaire du bleu patenté à 630 nm.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Physique-Chimie Terminale Spécialité

Pour s'échauffer - Pour commencer

Savoir-faire - Parcours d'apprentissage