Les icebergs sont d'énormes masses de glace flottante provenant de la dislocation des glaciers polaires.
L'expression « la partie immergée de l'iceberg » est utilisée dans le langage courant pour désigner la partie cachée d'une situation.
On considère un iceberg de volume V. On notera V_{i} son volume immergé. On négligera la poussée d'Archimède exercée par l'air sur la partie émergée.

Photographie d'icebergs flottant sur une eau bleu foncé. Reflets des icebergs dans l'eau. Paysage polaire.

1. Donner l'expression du poids \overrightarrow{P} de l'iceberg en fonction des données et l'expression de la poussée d'Archimède \overrightarrow{\varPi} exercée par l'eau de mer sur l'iceberg.

2. Schématiser l'iceberg et représenter les forces s'exerçant sur lui.

Cliquez pour accéder à une zone de dessin

3. En considérant que l'iceberg est à l'équilibre, en déduire l'expression du rapport \frac{V_{i}}{V} en fonction de \rho_{\text {glace }} et \rho_{\text {mer }}.

4. Effectuer l'application numérique. Expliquer l'expression « la partie immergée de l'iceberg ».

Doc.
Poussée d'Archimède La poussée d'Archimède est une force exercée sur tout objet en partie ou entièrement immergé, s'exprimant par la relation :

\overrightarrow{\varPi}=-\rho_{\text {fluide }} · V_{i} · \overrightarrow{g}

\overrightarrow{\varPi} : poussée d'Archimède de norme \varPi (N)
\rho_{\text {fluide }} : masse volumique du fluide (kg·m^-3)
V_{i} : volume immergé dans le fluide (m³)
\overrightarrow{g} : champ de pesanteur de norme g (N·kg^-1)

Données

Masse volumique de la glace : \rho_{\text {glace }}=900 kg·m^-3
Masse volumique de l'eau de mer : \rho_{\text {mer }}=1023 kg·m^-3

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Accélérateur d'ions

✔ VAL : Analyser des résultats

Un accélérateur linéaire est constitué d'une source S d'ions et d'une succession de tubes séparés par de petits interstices. L'accélération se fait dans chaque interstice grâce à un champ électrique \overrightarrow{E} et le champ opposé \overrightarrow{E^{\prime}}. Un générateur de tension alternative permet de changer le signe des charges des tubes à intervalle de temps régulier. Ce changement se fait quand les particules se trouvent au milieu du tube.

1. Expliquer pourquoi un ion est accéléré lorsqu'il passe dans l'interstice entre deux tubes.

2. Justifier que la vitesse est constante à l'intérieur d'un tube.

3. Expliquer pourquoi la durée de passage \Delta t d'un ion est la même pour tous les tubes. En déduire pourquoi les tubes doivent avoir des longueurs de plus en plus importantes.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Machine d'Atwood

✔ REA/MATH : Intégrer

George Atwood (1745-1807), physicien anglais enseignant à Cambridge, a proposé un dispositif permettant d'étudier la chute des corps en ralentissant leur mouvement.
La machine se compose de deux solides de masses respectives m_{1} et m_{2}, reliés par un fil. La position des centres de masse des solides est repérée par un axe (\text Oz) vertical.
On suppose que la tension de la corde est la même de part et d'autre de la poulie. Les frottements de l'air sont négligés.

Retrouvez ici
un simulateur de cette expérience.

1. Faire le bilan des forces s'exerçant sur le système de masse m_1 puis sur le système de masse m_{2}.

2. Compte tenu du dispositif, comparer les vecteurs accélération des deux solides.

3. Montrer que l'accélération d'un des solides est :

a=\frac{m_{2}-m_{1}}{m_{2}+m_{1}} · g

4. Calculer a.

5. Expliquer pourquoi ce dispositif a pu permettre aux étudiants de Georges Atwood d'étudier plus facilement la chute des corps.

Données

Masse des solides : m_{1} = 300 g et m_{2} = 500 g
Intensité de pesanteur : g = 9,81 N·kg^-1

Détails du barème
TOTAL / 4,5 pts

1 pt

1. Réaliser le bilan des forces exercées sur les solides.

0,5 pt

2. Justifier que les deux vecteurs accélération sont opposés.

1 pt

3. Appliquer la deuxième loi de Newton à chaque système et projeter sur l'axe vertical.

0,5 pt

3. Écrire une seule égalité en considérant que les accélérations sont les mêmes.

0,5 pt

3. Indiquer que la tension exercée par le fil est la même, simplifier l'égalité et donner l'expression.

0,5 pt

4. Effectuer un calcul.

0,5 pt

5. Faire le lien entre le résultat numérique et la situation décrite dans le texte.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28

Copie d'élève à commenter

Proposer une justification pour chaque erreur relevée par le correcteur.

Un avion humanitaire doit larguer un colis de denrées destinées à des civils en zone sinistrée. Il vole horizontalement à une vitesse constante de 600 km·h^-1 et à une altitude de 500 m. À t = 0 s, il largue le colis. On néglige les actions de l'air.

Donnée

Intensité de pesanteur : g = 9,81 N·kg^-1

1. Préciser la vitesse du colis dans le référentiel terrestre à t = 0 s.

La vitesse initiale du colis est \color{red}\cancel{\color{black}{\mathrm{nulle}}}.

2. Montrer que l'équation de la trajectoire du colis est :

y=-\frac{g}{2 v_{0}^{2}} · x^{2}+H

D'après la deuxième loi de Newton :
\overrightarrow{P}=m · \vec{a}
On a donc \color{red}\cancel{\color{black}{a = g}} ce qui conduit à :
Attention aux oublis de vecteurs
\color{red}\cancel{\color{black}{v_{x}(t) = 0}} et v_{y}(t) = -g · t
Donc :
x(t) = 0 et y(t) = \color{red}\cancel{\color{black}{-2 g · t}}

3. Exprimer la distance D du point de chute souhaité depuis laquelle l'avion doit larguer le colis.

0=-\frac{9}{2 v_{0}^{2}} \cdot D^{2}+H donc D=\color{red}\cancel{\color{black}{\frac{2 H \cdot v_{0}^{2}}{g}}}

4. Calculer la vitesse v_{c} du colis au moment où il touche la cible.

D'après le principe de conservation de \color{red}\cancel{\color{black}{\mathrm{l'énergie\;cinétique}}} :

\color{red}\cancel{\color{black}{\frac{1}{2} m · v_{0}-\frac{1}{2} m · v_{c}^{2}=m · g · H}}

\color{red}\cancel{\color{black}{v_{c}=\sqrt{2 g · H}=99 \mathrm{m} · \mathrm{s}^{-1}}}

5. Proposer une explication au fait que ce sont les hélicoptères qui sont privilégiés pour ces largages.

Afin que le colis tombe à une vitesse plus faible. Il faut justifier.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
Jeu d'enfants

✔ COM : Rédiger correctement une résolution d'exercice

Deux enfants jouent sur une terrasse surélevée avec des palets qu'ils lancent. Alex lance son palet horizontalement en le faisant glisser sur la terrasse, alors qu'Amélia le lâche du haut de la terrasse sans vitesse initiale. Alex pense que son palet met moins de temps que celui d'Amélia pour aller de la terrasse au sol, mais la durée de chute est trop courte pour arriver à la chronométrer.

Déterminer lequel a raison en justifiant la réponse.

Doc. 1
Schéma de la terrasse

Doc. 2
Coup de pouce Pour pouvoir résoudre l'exercice, il est nécessaire d'effectuer un certain nombre d'étapes. On pourra les trouver par soi‑même ou bien s'aider du protocole suivant :

établir l'équation de la trajectoire du centre de masse du palet dans les deux situations ;
établir l'équation de la trajectoire du centre de masse du palet dans les deux situations ;
conclure.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Angry Birds

✔ VAL : Analyser des résultats

Le jeu vidéo Angry Birds utilise des oiseaux comme projectiles afin de faire tomber une structure en bois sur laquelle se trouve un cochon. Le joueur tire sur l'élastique sur lequel est posé l'oiseau afin de le propulser. La trajectoire s'affiche, lui permettant de rectifier son tir à l'essai suivant.

Capture d'écran Angry Birds 2 : un oiseau rouge est prêt à être lancé par une fronde vers une structure en bois où se trouve un cochon vert.

On considère un tableau du jeu pour lequel l'oiseau doit franchir un mur avant d'atteindre sa cible. L'épaisseur du mur sera négligée, ainsi que les actions de l'air. Dans un repère cartésien (\mathrm{O}, \overrightarrow{i}, \overrightarrow{k}) dont l'origine \text{O} est positionnée au niveau du sol, au pied du lance‑oiseau, les coordonnées du vecteur vitesse \overrightarrow{v} de l'oiseau au cours de son vol sont :
\left\{\begin{array}{l} v_{x}(t)=v_{0} · \cos (\alpha) \\ v_{z}(t)=-g · t+v_{0} · \sin (\alpha) \end{array}\right.

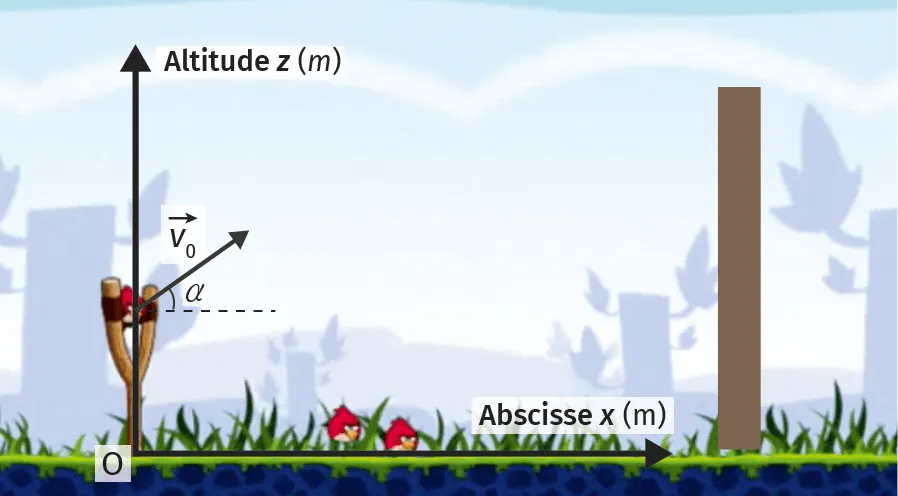
Schéma Angry Birds : oiseau rouge lancé par une fronde, trajectoire parabolique illustrant vitesse, angle et coordonnées (x, z).

1. Expliquer sur quelles grandeurs physiques le joueur peut agir grâce à l'élastique.

On donne à l'oiseau une vitesse initiale v_{0}. On cherche à déterminer l'angle de tir \alpha_{\min } permettant de franchir le mur en restant à l'altitude la plus basse possible.

2. a. Au moment du franchissement du mur, préciser à quel point particulier de la trajectoire se trouve l'oiseau.

b. En déduire la valeur de v_{z} et l'expression de t_{s}, instant au cours duquel l'oiseau franchit le mur.

c. Exprimer littéralement z\left(t_{s}\right), puis en déduire la valeur minimale de l'angle de tir \alpha_{\min }.

3. Si le tir est réalisé avec l'angle de tir minimal, déterminer si la structure en bois peut tomber. On considérera que la structure tombe si elle est touchée entre z_{1}=0,70 m et z_{2}=1,20 m.

Données

Masse de l'oiseau : m = 700 g
Hauteur du mur : h = 1,20 m
Altitude initiale de l'oiseau : z_{0}=50 cm
Distance entre le lance‑oiseau et le mur : d_{1}=2,0 m
Distance entre le lance‑oiseau et la structure : d_{2}=3,0 m
Vitesse initiale maximale : v_{0}=6,0 m·s^-1
Intensité de pesanteur : g = 9,81 N·kg^-1

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Spectromètre de masse

✔ APP : Faire des prévisions à l'aide d'un modèle
✔ RAI/MOD : Utiliser avec rigueur le modèle de l'énergie

La spectrométrie de masse est une technique d'analyse par mesure de masse. Elle consiste à ioniser les molécules, puis à exercer sur elles une force via un champ électrique. Les molécules de masses différentes, de par leur inertie différente, suivent des trajectoires différentes, ce qui permet de les séparer et de les détecter indépendamment. On peut ainsi, par exemple, déterminer le rapport isotopique d'un échantillon.

La méthode la plus simple (mais pas la plus précise) de spectrométrie de masse consiste à accélérer la molécule ionisée dans un champ homogène et uniforme pendant un certain temps puis à mesurer la vitesse atteinte via une mesure de temps de vol (temps nécessaire pour parcourir une distance connue).

Dans tout l'exercice, le poids sera négligé. On considère une molécule de masse m au repos dans le spectromètre de masse. Un électron lui est arraché, puis elle est accélérée dans un champ uniforme \vec{E} créé par une tension U entre deux armatures séparées par une distance d. Ensuite, la molécule ne subit plus aucune force jusqu'à atteindre le détecteur. Pendant cette deuxième phase, la molécule parcourt une distance l, et la durée de cette phase (le temps de vol) sera notée \Delta t_{vol}.

I. Calcul via la seconde loi de Newton

On choisit l'axe (Ox) tel que \vec{E} = E \cdot \vec{u_x}. La position de la molécule à l'instant initial est choisie comme origine du repère.

1. En appliquant la seconde loi de Newton, exprimer la valeur de l'accélération a de la molécule suivant l'axe (Ox).

2. En déduire l'équation horaire de la valeur de la vitesse v et de la coordonnée x de la molécule.

3. En déduire l'expression de la vitesse v en fonction de la position x.

4. En déduire l'expression de la vitesse v_1 atteinte par la molécule à la fin de la première phase en fonction de U, m et q.

II. Calcul via le théorème de l'énergie cinétique

5. En appliquant le théorème de l'énergie cinétique, déterminer l'expression de la vitesse atteinte par la molécule à la fin de la première phase en fonction de U, m et q.

III. Temps de vol

6. Justifier que dans la deuxième phase, la vitesse de la molécule est constante.

7. Exprimer le temps de vol en fonction de la vitesse v atteinte par la molécule, puis des données.

8. Calculer le temps de vol pour une molécule de méthane \mathrm{CH}_{4} dont l'atome de carbone est un atome de carbone 12, puis pour une molécule de méthane dont l'atome de carbone est un atome de carbone 13.

Données

Expression de la force subie par une particule de charge q dans un champ uniforme \vec{E} : \vec{F_e} = q \cdot \vec{E}
Expression du travail de la force électrique reçu par une particule de charge q dans un champ uniforme : W_e = q \cdot E
Expression de l'intensité du champ électrique uniforme entre deux armatures séparées par une distance d : E = \dfrac{U}{d}
Charge élémentaire : e = 1{,}60 \times 10^{-19} C
Masse de l'atome de carbone 12, 12C : M_{^{12}\text{C}} = 2{,}009 \times 10^{-26} kg
Masse de l'atome de carbone 13, 13C : M_{^{13}\text{C}} = 2{,}176 \times 10^{-26} kg
Masse de l'atome d'hydrogène : M_H = 1{,}673 \times 10^{-27} kg
Caractéristiques du spectromètre de masse : U = 15 kV et l = 1{,}5 m

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

B
Expérience de Millikan

✔ RAI/ANA : Construire un raisonnement
✔ REA/MATH : Résoudre une équation différentielle

Le physicien américain R. Millikan a reçu le prix Nobel de physique en 1923 pour avoir démontré que la charge électrique d'un objet ionisé est toujours un multiple d'une certaine valeur et pour avoir mesuré cette valeur. Son dispositif constitue la toute première expérience de mesure de la charge élémentaire e.

Pour cela, il arrache un ou plusieurs électrons (par irradiation X) à des gouttelettes d'huile qu'il fait alors tomber dans un champ électrique \overrightarrow{E} = E \cdot \overrightarrow{u_x} dont il peut changer l'intensité et la polarité. Ensuite, il mesure la vitesse de chaque gouttelette grâce à une simple mesure de distance parcourue par unité de temps à l'aide d'un microscope. Cette mesure lui permet de déterminer la charge de la gouttelette.
On définit l'axe (Ox) vertical, dirigé vers le bas.

La gouttelette (de masse m, de volume V, de rayon r et de charge q) est soumise à quatre forces :

son poids \overrightarrow{P} = m \cdot g \cdot \vec{u_x} ;
la poussée d'Archimède \overrightarrow{\Pi} = - V \cdot \rho_{air} \cdot g \cdot \overrightarrow{u_x} ;
la force électrique : \overrightarrow{F_e} = q \cdot E \cdot \overrightarrow{u_x} ;
la force de frottement de l'air \overrightarrow{f} = - 6 \ \pi \cdot \eta \cdot r \cdot \overrightarrow{v}.

Le symbole \eta désigne un paramètre constant au cours de l'expérience, correspondant à la viscosité de l'air.

Questions préliminaire :

1. Montrer que la somme du poids et de la poussée d'Archimède est équivalente à une force de pesanteur \overrightarrow{P'} = m \cdot g' \cdot \vec{u_x} avec g' = g \cdot \left(1 - \dfrac{\rho_{air}}{\rho_h}\right).

2. Justifier que pour une précision de l'ordre de 1 %, on peut négliger la poussée d'Archimède.

I. Évolution temporelle de la vitesse

3. À l'aide de la seconde loi de Newton, déterminer l'équation différentielle vérifiée par v.

4. Montrer que la solution de cette équation est v = A \cdot \exp \left( - \dfrac{t}{\tau} \right) + v_{lim} et donner les expressions de \tau et v_{lim}.

5. Montrer que A = v_0 - v_{lim}, où v_0 est la vitesse de la goutte à l'instant initial.

6. Tracer l'allure de la courbe en faisant apparaître v_0 et v_{lim}.

Cliquez pour accéder à une zone de dessin

7. On considère que la vitesse limite est atteinte lorsque t_{lim} = 10 \ \tau. Calculer cette date pour une gouttelette de rayon r = 2{,}0 µm.

II. Exploitation des résultats

8. Une fois que la vitesse limite est atteinte, la gouttelette tombe à vitesse constante. Justifier que la somme des forces est nulle.

On note q = n \cdot e la charge de la gouttelette, où n est le nombre d'électrons arrachés.

9. Montrer que que la vitesse limite s'écrit v_{lim} = a \cdot n \cdot e + b, où a et b sont des coefficients constants. Et donner l'expression de a et b.

10. À l'aide du doc. 2, déterminer la valeur de b. En déduire la valeur de r.

11. À l'aide du doc. 2, déterminer la valeur de e.

Doc. 1
Équations différentielles linéaires du premier ordre Une équation différentielle de la forme \dfrac{\text{d} v}{\text{d}t} = K - \dfrac{v}{\tau} où K et \tau sont des constantes, admet comme solutions v = A \cdot \exp\left(-\dfrac{t}{\tau}\right) + K \cdot \tau où A est une constante dépendant des conditions initiales.

Doc. 2
Résultats expérimentaux

Données

Expression du volume d'une sphère de rayon r : V = \dfrac{4}{3} \ \pi \cdot r^3
Intensité de pesanteur : g = 9{,}81 N·kg^-1
Viscosité de l'air : \eta = 1{,}9 \times 10^{-5} kg·m^-1·s^-1
Masse volumique de l'air : ρ_{air} = 1{,}2 kg·m^-3
Masse volumique de l'huile : ρ_h = 9{,}0 \times 10^2 kg·m^-3
Intensité du champ électrique utilisé : E = 6{,}0 \times 10^5 V·m^-1

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Physique-Chimie Terminale Spécialité

Pour s'entraîner

24Partie immergée de l'iceberg

25Championnat de fléchettes en QCM

26Accélérateur d'ions

27Machine d'Atwood

Détails du barème TOTAL / 4,5 pts

28 Copie d'élève à commenter

29Jeu d'enfants

30Angry Birds

ASpectromètre de masse

BExpérience de Millikan

Une erreur sur la page ? Une idée à proposer ?

24
Partie immergée de l'iceberg

25
Championnat de fléchettes en QCM

26
Accélérateur d'ions

27
Machine d'Atwood

Détails du barème
TOTAL / 4,5 pts

28

Copie d'élève à commenter

29
Jeu d'enfants

30
Angry Birds

A
Spectromètre de masse

B
Expérience de Millikan