	Pour commencer	Différenciation	Pour s'entraîner
Savoir définir et exploiter les vecteurs vitesse et accélération	10 15	17 18 19
Savoir exploiter les expressions de la vitesse et l'accélération dans le repère de Frenet	9		21
Savoir caractériser le vecteur accélération	14		28

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour s'échauffer

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

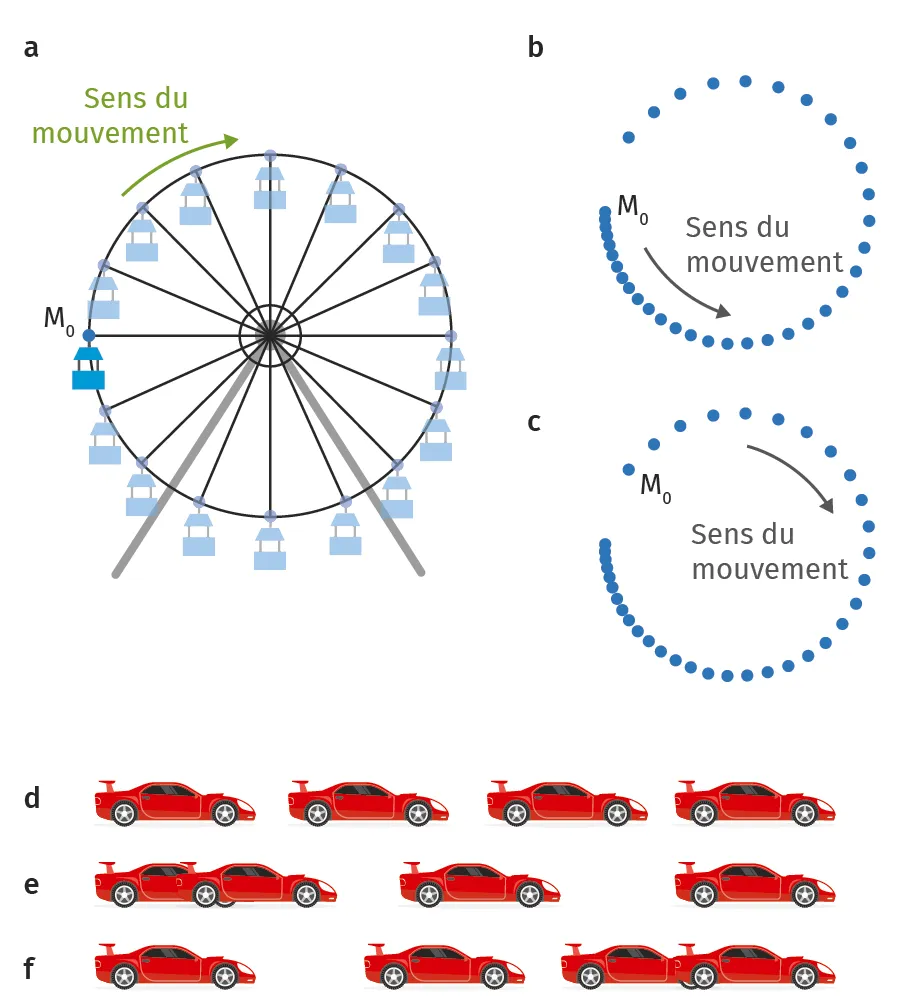
5
Description d'un mouvement

Pour les chronophotographies ci-dessous, décrire le mouvement des systèmes dont les positions successives se succèdent à intervalle de temps régulier.

Illustration: schémas chronophotographiques. Mouvement d'une grande roue, points et voitures. Sens de déplacement indiqué.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Accélération d'une voiture

Déterminer les accélérations moyennes des voitures suivantes.

1. Une voiture de course passant de 0 à 100 km·h^-1 en 3,0 s.

2. Une voiture subissant un choc durant 70 ms tel que \Delta v = 16 km·h^-1.

3. Une voiture roulant à 30 km·h^-1 subissant un arrêt brutal en un dixième de seconde.

4. Une voiture prenant un rond-point de 30 m de diamètre à 30 km·h^‑1 (vitesse constante).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Nœud

Le nœud, noté (nd), est une unité de vitesse utilisée par les marins. Le record du monde de vitesse à la voile en kitesurf sur 500 m avoisine les 60 nd.

Convertir cette vitesse en (m·s^-1), puis en (km·h^-1).

Données

Conversion d'unité : 1 nd = 1 852 m·h^-1

Photographie de deux kitesurfeurs sur l'océan. Cerfs-volants colorés. Sport nautique.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Pour commencer

Vocabulaire

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Vocabulaire adéquat

✔ APP : Maîtriser le vocabulaire du cours

Pour chacune des propositions suivantes, préciser si elles sont vraies ou fausses, puis corriger les propositions fausses.

a. Le vecteur vitesse \vec{v} est toujours tangent à la trajectoire.

b. Les vecteurs position \overrightarrow{\text{OM}} et vitesse \vec{v} ont toujours le même sens pour un mouvement rectiligne.

c. L'accélération est toujours nulle pour un mouvement rectiligne.

d. Un mouvement rectiligne admet un vecteur position \overrightarrow{\text{OM}} de sens contraire à celui de son accélération \vec{a}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Mouvement circulaire

✔ APP : Maîtriser le vocabulaire du cours

Pour chacune des propositions suivantes, préciser si elles sont vraies ou fausses, puis corriger les propositions fausses.

a. Dans le repère de Frenet, \overrightarrow{N} est tangent à la trajectoire.

b. L'accélération \vec{a} est nulle pour les mouvements circulaires uniformes.

c. Le vecteur accélération est toujours centripète, c'est-à-dire orienté vers le centre de la trajectoire pour les mouvements circulaires.

d. Le vecteur accélération \vec{a} peut être centrifuge, sous certaines conditions, pour un mouvement circulaire.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Caractérisation d'un mouvement

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
Bons adjectifs

✔ APP : Maîtriser le vocabulaire du cours

Décrire les mouvements dont les trajectoires sont représentées ci-dessous à l'aide d'un ou de plusieurs de ces qualificatifs :

rectiligne ;

impossible ;

décéléré ;

curviligne ;

accéléré ;

uniforme.

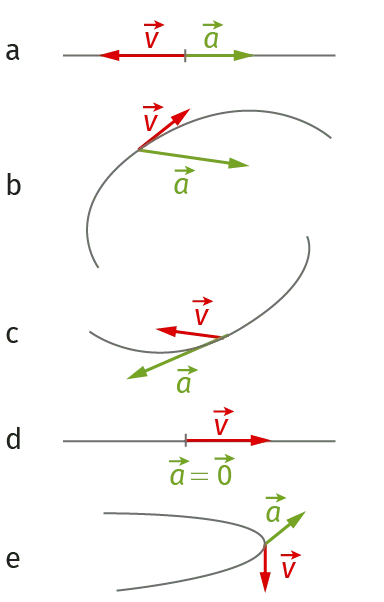
Mouvement a :

Mouvement b :

Mouvement c :

Mouvement d :

Mouvement e :

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
Représentation graphique

✔ VAL : Faire preuve d'esprit critique

1. Déterminer quels graphes correspondent aux évolutions de la position x(t), de la vitesse v(t) et de l'accélération a(t) d'un système ayant un mouvement rectiligne uniforme.

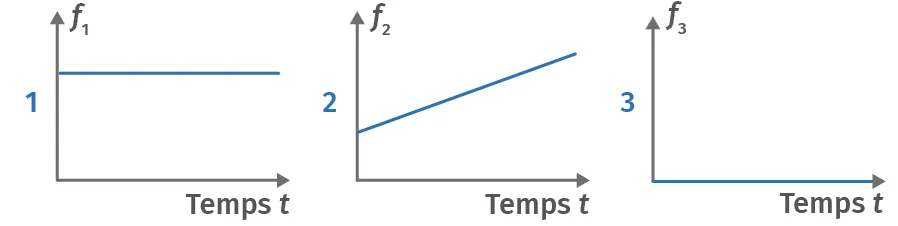
Illustration : trois graphiques de fonctions mathématiques. Le premier est une droite horizontale, le second une droite ascendante, le troisième une droite horizontale.

2. Préciser dans quel sens suivant l'axe (Ox) se déplace le système.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
Route du Rhum

✔ APP : Maîtriser le vocabulaire du cours

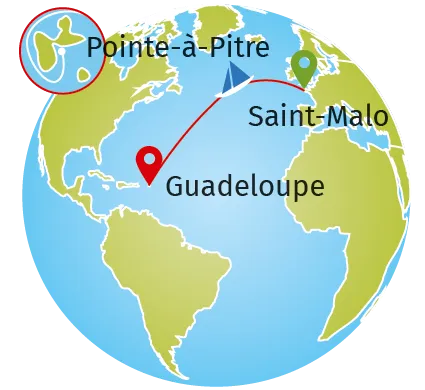
Carte illustrant le parcours de la Route du Rhum, de Saint-Malo à Pointe-à-Pitre en Guadeloupe.

L'orthodromie (route la plus courte formant un arc de cercle) reliant Saint‑Malo à Pointe‑à‑Pitre est dessinée ci-contre. Elle est de 3 452 M (le symbole M signifiant mille marin). En 2018, Francis Joyon bat le record de la traversée en 7 j 14 h 21 min et 47 s à la vitesse moyenne de 23,95 nd, le symbole (nd) signifiant nœud.

1. Parcourue à vitesse constante, décrire cette trajectoire dans le référentiel géocentrique.

2. Rechercher sur Internet la valeur d'un mile marin (M).

3. Préciser si le trajet suivi par le skipper est orthodromique.

Revivez la route du Rhum 2018
et découvrez la différence entre

loxodromie et orthodromie

Donnée

Définition du nœud, noté (nd) : 1 nd = 1 852 m·h^-1

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
Conditions initiales d'un mouvement

✔ REA/MATH : Utiliser des outils mathématiques

Les trois schémas ci-dessous représentent les conditions initiales de trois mouvements.

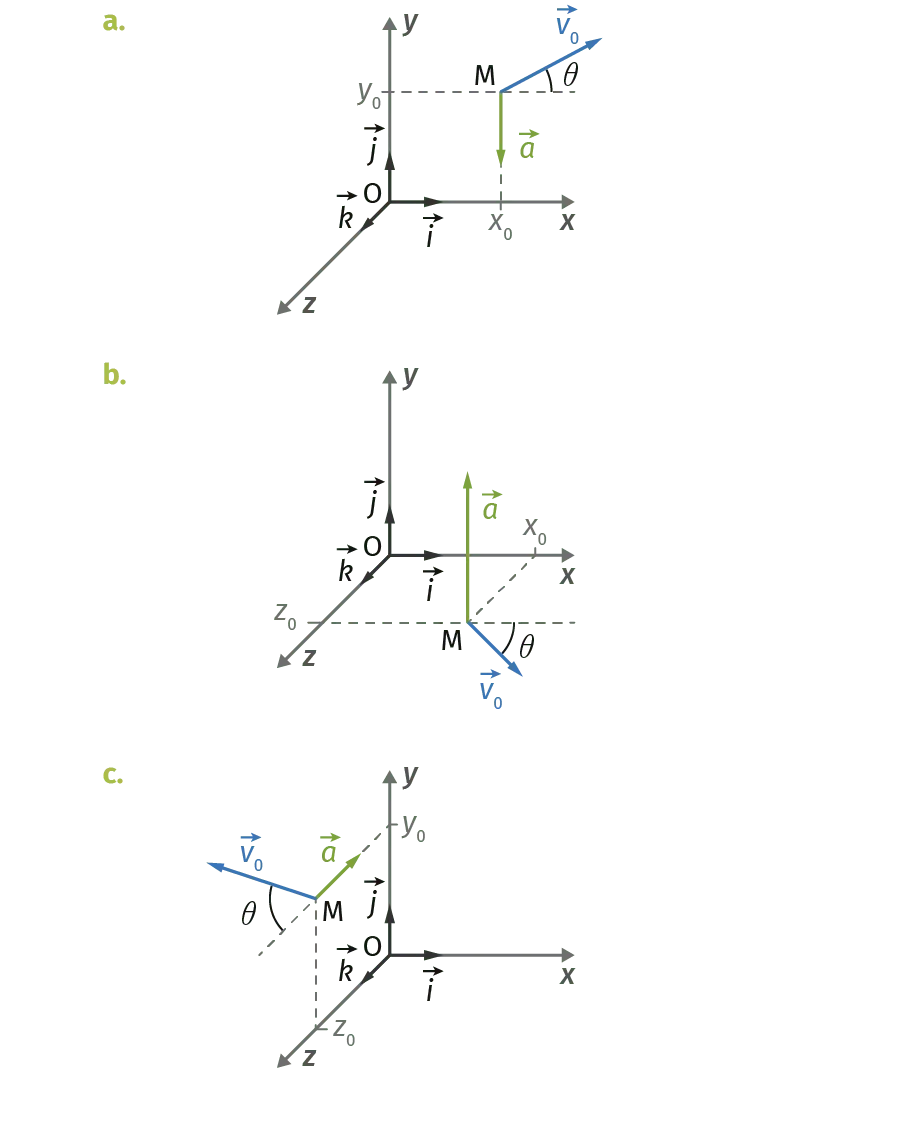
Schéma : 3 graphiques 3D montrent des conditions initiales de mouvement. Vecteurs, axes (x, y, z), angles θ.

Déterminer les coordonnées des vecteurs vitesse initiale et accélération pour les trois situations représentées ci-dessus.

a.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
Aiguilles d'une horloge

✔ APP : Maîtriser le vocabulaire du cours

Une coccinelle se tient immobile sur l'aiguille des secondes d'une horloge. Cette aiguille mesure 20,0 cm.

Photographie d'une horloge analogique indiquant 15h00, une coccinelle est posée sur l'aiguille des minutes.

1. Préciser le référentiel dans lequel la coccinelle est immobile.

2. Donner la nature du mouvement de la coccinelle dans le référentiel de la pièce dans laquelle se trouve l'horloge.

3. Préciser les caractéristiques des vecteurs vitesse et accélération de la coccinelle dans le référentiel de la pièce.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exploitation des lois horaires

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Chute de la tour Eiffel

✔ REA/MATH : Dériver

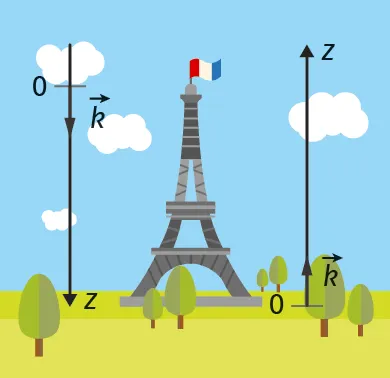
Illustration: la Tour Eiffel avec des axes z et k pour expliquer un concept mathématique ou physique.

On étudie le mouvement d'un objet lâché depuis le troisième étage de la tour Eiffel, dont l'altitude au cours du temps est décrite par l'équation horaire suivante :

z(t) = - \dfrac{a}{2} \cdot t^2 + h_3

1. Des deux repères représentés sur la photo, identifier celui choisi pour la modélisation de la coordonnée z(t). Justifier.

2. Déterminer la composante du vecteur vitesse v_z(t).

3. En déduire les normes des vitesses de l'objet au moment où il atteint le deuxième étage, puis le premier étage.

4. Déterminer la durée de la chute jusqu'au sol.

Donnée

Hauteur du premier étage : h_1 = 58 m
Hauteur du deuxième étage : h_2 = 116 m
Hauteur du troisième étage : h_3 = 276 m
Coefficient : a = 9{,}8 m·s^-1

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
Mouvement rectiligne accéléré

✔ REA/MATH : Dériver

Un système, assimilé à un point M, se déplace le long d'un axe (\text{O}x), en un mouvement rectiligne. On repère celui-ci par son abscisse x(t) d'équation horaire :

x(t) = - \dfrac{a}{2} \cdot t^2 + v_0 \cdot t + x_0

Ici, a = 8{,}0 m·s^-2, v_0 = 16 m·s^-1 et x_0 = 5{,}0 m.

1. Situer le système à l'instant initial t_0 = 0 s.

2. Exprimer le vecteur vitesse \vec{v}(t) dans le repère (\text{O}\:,\vec{i}) et sa norme v(t) en fonction du temps.

3. Déterminer la date et la position d'arrêt du système.

4. Calculer à quel instant le système passe par l'origine.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

A
Exploitation des lois horaires

✔ REA/MATH : Dériver

Le centre de masse d'un solide lancé vers le haut en ligne droite le long d'un axe vertical \text{(Oz)} dirigé vers le haut est repéré par son altitude :

z(t) = - \dfrac{a}{2} \cdot t^2 + v_0 \cdot t + h

Les coefficients sont égaux à a = 10{,}0 m·s^-2, v_0 = 30 m·s^-1 et h = 2{,}0 m.

1. Déterminer les conditions initiales du lancer.

2. Exprimer les vecteurs vitesse et accélération, ainsi que leur norme, dans le repère (\text{O}, \ \overrightarrow{k}).

3. Donner les caractéristiques des vecteurs position, vitesse et accélération au sommet \text{S} de la trajectoire.

4. Quelle vitesse atteint le système lorsqu'il touche le sol ?

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Une notion, trois exercices
Différenciation

Savoir-faire : Savoir définir et exploiter les vecteurs vitesse et accélération

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
Mouvement rectiligne uniforme

✔ REA/MATH : Dériver

Un point mobile \text{M} est suivi par enregistrement dans un repère (\text{O}\:\vec{i}\:,\vec{j}). La modélisation de son mouvement fournit les équations horaires suivantes : x(t) = - v_0 \cdot t + x_0 et y(t) = y_0 avec v_0 = 8 m·s^-1, x_0 = 4 m et y_0 = 1 m.

1. Exprimer les coordonnées du vecteur position initiale.

2. Exprimer les coordonnées du vecteur vitesse et caractériser le mouvement.

3. Calculer la vitesse \text{} en (-12 m ; 1 m).

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
Mouvement parabolique

✔ REA/MATH : Dériver

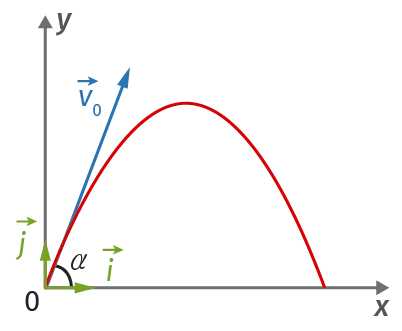
Graphique : trajectoire parabolique rouge, vecteurs vitesse et accélération indiqués.

Un point \text{M} adoptant une trajectoire parabolique admet comme équations horaires :
x(t) = v_{0x} \cdot t et y(t) = - \dfrac{a_y}{2} \cdot t^2 + v_{0y} \cdot t avec v_{0x} = 15{,}3 m·s^-1, a_y =9{,}81 m·s^-2 et v_{0y} = 12{,}9 m·s^‑1.

1. Exprimer les coordonnées du vecteur vitesse.

2. Montrer que la vitesse initiale du point \text{M} vaut v_0 = 20{,}0 m·s^-1.

3. En déduire l'angle \alpha formé par le vecteur vitesse initiale \vec{v_0} avec l'axe horizontal.

Données

Expression de la tangente de l'angle \alpha : \tan(\alpha) = \dfrac{v_{0y}}{v_{0x}}

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Mouvement circulaire

✔ REA/MATH : Dériver

Un point \text{M} décrit une trajectoire dont les équations horaires de position sont x(t) = R \cdot \cos(\omega \cdot t) et y(t) = R \cdot \sin(\omega \cdot t) avec R = 2 m, \omega = 5 rad·s^-1.

1. Montrer que la trajectoire est circulaire.

2. Déterminer les caractéristiques du vecteur vitesse à t = 0s.

Données

Équation d'un cercle de centre \text{O} (0 m ; 0 m) : x^2 + y^2 = R^2
Dérivées usuelles : \cos(u)' = -u' \cdot \sin(u) et \sin(v)' = v' \cdot \cos(v)

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Physique-Chimie Terminale Spécialité

Pour s'échauffer - Pour commencer

Savoir-faire - Parcours d'apprentissage