Physique-Chimie Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Préparation aux épreuves du Bac
1. Constitution et transformations de la matière
Ch. 1
Modélisation des transformations acide-base
Ch. 2
Analyse physique d'un système chimique
Ch. 3
Méthode de suivi d'un titrage
Ch. 4
Évolution temporelle d'une transformation chimique
Ch. 5
Évolution temporelle d'une transformation nucléaire
BAC
Thème 1
Ch. 6
Évolution spontanée d'un système chimique
Ch. 7
Équilibres acide-base
Ch. 8
Transformations chimiques forcées
Ch. 9
Structure et optimisation en chimie organique
Ch. 10
Stratégies de synthèse
BAC
Thème 1 bis
2. Mouvement et interactions
Ch. 11
Description d'un mouvement
Ch. 12
Mouvement dans un champ uniforme
Ch. 13
Mouvement dans un champ de gravitation
Ch. 14
Modélisation de l'écoulement d'un fluide
BAC
Thème 2
3. Conversions et transferts d'énergie
Ch. 15
Étude d’un système thermodynamique
Ch. 16
Bilans d'énergie thermique
BAC
Thème 3
4. Ondes et signaux
Ch. 17
Propagation des ondes
Ch. 18
Interférences et diffraction
Ch. 19
Lunette astronomique
Ch. 20
Effet photoélectrique et enjeux énergétiques
Ch. 21
Évolutions temporelles dans un circuit capacitif
BAC
Thème 4
Annexes
Ch. 22
Méthode
Chapitre 13
Exercices
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Famille transneptunienne en QCM
✔ VAL
: Faire preuve d'esprit critique
Au-delà de l'orbite de Neptune, deux planètes naines, Hauméa (\text{H}) et Makémaké (\text{M}), ont été découvertes dans la ceinture de Kuiper entre 2004 et 2005. Choisir la (ou les) bonne(s) réponse(s).
1. La planète \text{H} est plus éloignée que \text{M} du Soleil, en supposant leur trajectoire circulaire :
2. Si une des planètes a une trajectoire elliptique, alors :
3. En ne considérant que l'action exercée par le Soleil, la norme du vecteur vitesse de chaque planète :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Galileo
✔ REA : Utiliser un modèle
Similaire au système américain GPS, Galileo est un système de positionnement. Il permet d'obtenir sa position à l'aide d'une trentaine de satellites. En utilisant la 2e loi de Kepler dans le repère de Frenet, on montre que la vitesse du satellite d'altitude h est égale à :
v^{2}=G \cdot \frac{M_{\text{T}}}{R_{\text{T}}+h}
1. Rappeler la définition de la période de révolution.
2. Donner la relation qui lie la vitesse d'un satellite à sa période de révolution T.
3. En déduire l'expression de la période T en fonction de G, M_\text{T}, R_\text{T} et h.
Histoire des sciences
Spoutnik 1 est le premier objet envoyé dans l'espace le 4 octobre 1957. Il inaugure la course technologique effrénée opposant l'URSS et les États-Unis. Cependant, 50 ans après, les nombreux débris issus de plus de 5 000 lancements constituent un risque et doivent être surveillés pour éviter tout incident.
Découvrez le fonctionnement de Galileo en vidéo en .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Trajectoire d'une comète
✔ APP : Faire un schéma
La trajectoire d'une comète est tracée ci-dessous dans le référentiel héliocentrique. On suppose que les durées de parcours entre les points \text{M}_1 et \text{M}^{\prime}_1 puis entre \text{M}_2 et \text{M}^{\prime}_2 sont égales. La comète est soumise à l'attraction gravitationnelle du Soleil. Toute autre action est négligée.
1. Après avoir identifié la forme de la trajectoire, préciser ce que représentent les points \text{F}_1, \text{F}_2 et \text{O}.
2. Déterminer sur quel parcours entre \text{M}_1\text{M}^{\prime}_1 ou \text{M}_2\text{M}^{\prime}_2 la vitesse de la comète est la plus importante.
Expliquer.
1. Après avoir identifié la forme de la trajectoire, préciser ce que représentent les points \text{F}_1, \text{F}_2 et \text{O}.
2. Déterminer sur quel parcours entre \text{M}_1\text{M}^{\prime}_1 ou \text{M}_2\text{M}^{\prime}_2 la vitesse de la comète est la plus importante.
Expliquer.
3. Représenter la force d'interaction gravitationnelle exercée sur la comète sur un point de la trajectoire.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Anneaux de Saturne
✔ APP : Faire des prévisions à l'aide d'un modèle
La planète Saturne est reconnaissable par ses anneaux. On suppose que chaque constituant gravite avec un mouvement uniforme où seule l'action exercée par Saturne est prise en compte.
1. Montrer que la vitesse d'un élément de l'anneau est donnée par :
2. Pour deux éléments d'éloignements distincts, préciser lequel est le plus rapide.
Détails du barème
1. Montrer que la vitesse d'un élément de l'anneau est donnée par :
v^{2}=\frac{G \cdot M_{\text{S}}}{r}
2. Pour deux éléments d'éloignements distincts, préciser lequel est le plus rapide.
Détails du barème
TOTAL / 6 pts
1 pt
1. Expression de la force d'interaction entre Saturne et un élément de l'anneau.1 pt
1. Appliquer la 2e loi de Newton à un élément pour déterminer son accélération.2 pts
1. Utiliser le repère de Frenet pour déterminer l'expression de la vitesse.2 pts
2. Analyser l'influence de la distance r.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27VOSTOK 1, premier vol spatial
✔ REA : Appliquer une formule
Le premier vol habité de l'histoire a été effectué le 12 avril 1961 depuis le cosmodrome de Baïkonour avec à son bord le cosmonaute Youri Gagarine.
La trajectoire du module est modélisée suivant une orbite circulaire d'altitude moyenne h =~225 km.
La trajectoire du module est modélisée suivant une orbite circulaire d'altitude moyenne h =~225 km.
1. Préciser la condition pour qu'un mouvement soit
uniforme.
2. Établir le bilan des forces exercées sur le module.
3. Montrer que l'expression de la vitesse orbitale du module est égale à :
2. Établir le bilan des forces exercées sur le module.
3. Montrer que l'expression de la vitesse orbitale du module est égale à :
v=\sqrt{\frac{G \cdot M_{\text{T}}}{R_{\text{T}}+h}}
4. Calculer la valeur de la vitesse du module.
5. En déduire la période de révolution du module.
5. En déduire la période de révolution du module.
Données
- Constante de gravitation universelle : \nobreakspace{G =~6{,}67 \times 10^{-11}} m3·kg-1·s-2
- Rayon de la Terre : R_\text{T} = 6\ 370 km
- Masse de la Terre : M_\text{T} = 5{,}97 \times 10 ^{24} kg
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Télescope spatial Hubble
✔ APP : Faire un schéma
Nommé en l'honneur d'Edwin Hubble (1889-1953), le télescope spatial Hubble (HST) décrit une orbite circulaire de 42 000 km de circonférence. Cette position dans l'espace permet au télescope d'effectuer des observations sans les contraintes dues à l'atmosphère terrestre.
1. Indiquer dans quel référentiel est décrite la trajectoire du télescope.
2. Nommer les forces qui s'exercent sur le HST. Indiquer celles que l'on peut négliger en justifiant la réponse.
Doc.
Télescope Hubble
Fruit d'une coopération entre la NASA et l'agence spatiale européenne, le télescope spatial Hubble (HST) est opérationnel depuis 1990.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Copie d'élève à commenter
Proposer une justification pour chaque erreur relevée par le correcteur.
Doc.
Satellite FORUM
Orbite polaire héliosynchrone.
Un réchauffement climatique est observé depuis le début du XXe siècle. Afin d'améliorer la compréhension de l'évolution climatique, l'agence spatiale européenne (ESA) étudie l'envoi d'un satellite FORUM (Far-Infrared Outgoing Radiation Understanding and Monitoring) pour mesurer le rayonnement infrarouge lointain émis par la Terre. Ce satellite se déplacera suivant une orbite polaire héliosynchrone quasicirculaire avec une altitude moyenne de 830 km.
1. Rappeler le domaine spectral des ondes utilisées.
Le domaine spectral de l'infrarouge lointain est compris entre \color{red}\sout{\color{black}{600}} et \color{red}\sout{\color{black}{800}} nm.
2. Déterminer le plan de l'orbite et l'altitude moyenne de FORUM sachant qu'il gravitera à une altitude environ 42 fois plus proche de la Terre qu'un satellite géostationnaire.
Au vu du nom de l'orbite polaire et du schéma, le plan de l'orbite contient l'axe des pôles terrestres et est perpendiculaire au plan équatorial. L'orbite géostationnaire a un rayon de \color{red}\cancel{\color{black}{36~000~\text{m}}}.
On en déduit que FORUM se déplace à une altitude égale à \color{red}\cancel{\color{black}{850~\text{m}}}.
3. Donner sa vitesse orbitale.
Le domaine spectral de l'infrarouge lointain est compris entre 600 et 800 nm.
v^{2}=\dfrac{G \cdot M_{\text{T}}}{r}
AN : \color{red}\cancel{\color{black}{y=\dfrac{6{,}67 \times 10^{-11} \times 5{,}97 \times 10^{24}}{830}}}
\color{red}\cancel{\color{black}{= 4{,}68 \mathrm{km} \cdot \mathrm{h}^{-1}}}
v^{2}=\dfrac{G \cdot M_{\text{T}}}{r}
AN : \color{red}\cancel{\color{black}{y=\dfrac{6{,}67 \times 10^{-11} \times 5{,}97 \times 10^{24}}{830}}}
\color{red}\cancel{\color{black}{= 4{,}68 \mathrm{km} \cdot \mathrm{h}^{-1}}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Altimétrie satellitaire
✔ RAI/ANA : Construire un raisonnement
Le niveau moyen global des océans est un indicateur majeur du réchauffement climatique. L'altimétrie satellitaire est une méthode de mesure importante, car elle permet d'assurer un suivi mondial précis et continu depuis 1993. Depuis son lancement en 2013, le satellite franco‑indien SARAL assure toujours cette mission.
1. Préciser le nom du référentiel galiléen dans lequel le mouvement du satellite peut être étudié.
2. En supposant une orbite circulaire, schématiser la trajectoire sans souci d'échelle.
2. En supposant une orbite circulaire, schématiser la trajectoire sans souci d'échelle.
Cliquez pour accéder à une zone de dessin
3. En déduire la nature du mouvement d'après la deuxième loi de Kepler.
4. Dans le cas de SARAL, préciser la direction prise par son vecteur accélération. Représenter le vecteur \vec{a}_{\mathrm{S}} sur le schéma.
4. Dans le cas de SARAL, préciser la direction prise par son vecteur accélération. Représenter le vecteur \vec{a}_{\mathrm{S}} sur le schéma.
Cliquez pour accéder à une zone de dessin
5. Montrer que le vecteur vitesse de SARAL a pour valeur :
6. Calculer l'altitude h du satellite SARAL à l'aide des données.
7. Préciser en le justifiant si SARAL est géostationnaire.
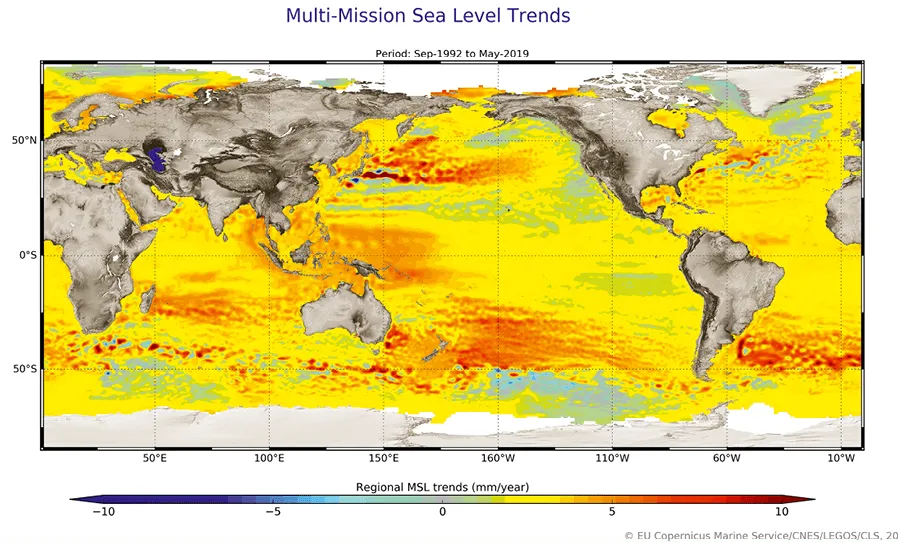Les zones rouges correspondent aux zones géographiques où le niveau moyen d'élévation est le plus important.
v_{s}=\sqrt{\frac{G \cdot M_{\text{T}}}{R_{\text{T}}+h}}
6. Calculer l'altitude h du satellite SARAL à l'aide des données.
7. Préciser en le justifiant si SARAL est géostationnaire.
Données
- Constante de gravitation universelle : \nobreakspace{G =6{,}67 \times 10^{-11}} m3·kg-1·s-2
- Masse du satellite SARAL : m_\text{S} = 400 kg
- Vitesse orbitale de SARAL : v_\text{S} =7{,}47 km·s-1
- Période de rotation de la Terre : T_\text{T} =23{,}93 h
- Rayon de la Terre : R_\text{T} = 6\ 370 km
- Masse de la Terre : M_\text{T} = 5{,}97 \times 10^{24} kg
- Expression du vecteur accélération dans le cas d'un mouvement circulaire :
\nobreakspace{\vec{a}\left(\begin{array}{c} \frac{\mathrm{d} v}{\mathrm{d} t} \\ \frac{v^{2}}{r} \end{array}\right)_{(G, \vec{T}, \vec{N})}}
Doc.
Cartographie du niveau d'élévation des océans
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Température de surface de la mer
✔ RAI/ANA : Utiliser et interpréter des documents
Le suivi de la mesure de la température de l'océan est important, car la température influe sur le transport océanique et le climat mondial. En plus des mesures in-situ (bouées, bateaux), les satellites à défilement comme MetOp et NOAA ou géostationnaires comme GOES et Meteosat permettent de réaliser des mesures sur une grande surface terrestre dans l'infrarouge.
On considère les satellites comme ponctuels et soumis à la seule interaction gravitationnelle terrestre. Leur mouvement est décrit dans le référentiel géocentrique suivant une orbite supposée circulaire de rayon r.
On considère les satellites comme ponctuels et soumis à la seule interaction gravitationnelle terrestre. Leur mouvement est décrit dans le référentiel géocentrique suivant une orbite supposée circulaire de rayon r.
1. Expliquer la différence possible entre un satellite géostationnaire et un satellite à défilement.
2. Représenter sans souci d'échelle la Terre, un satellite et sa trajectoire.
2. Représenter sans souci d'échelle la Terre, un satellite et sa trajectoire.
Cliquez pour accéder à une zone de dessin
3. Préciser l'hypothèse adoptée si on représente la Terre par un point O correspondant à son centre de masse.
4. Donner l'expression de la 3e loi de Kepler. Montrer qu'elle est cohérente avec la formule :
Le tableau ci-dessous regroupe les périodes T de révolution et les rayons r de la trajectoire des différents satellites utilisés pour créer les cartes de températures.
5. Expliquer en quoi ces mesures permettent de confirmer la 3e loi de Kepler.
4. Donner l'expression de la 3e loi de Kepler. Montrer qu'elle est cohérente avec la formule :
T=\sqrt{\frac{4 \pi^{2} \cdot r^{3}}{G \cdot M_{\text{T}}}}
Le tableau ci-dessous regroupe les périodes T de révolution et les rayons r de la trajectoire des différents satellites utilisés pour créer les cartes de températures.
5. Expliquer en quoi ces mesures permettent de confirmer la 3e loi de Kepler.
| Satellite | Rayon de l'orbite \boldsymbol{r} (km) | Période \boldsymbol{T} (s) |
| Goes 17 | 4{,}22 \times 10^{4} | 8{,}62 \times 10^{4} |
| Meteosat | 42{,}1 \times 10^{3} | 8{,}58 \times 10^{4} |
| Noaa 20 | 7{,}19 \times 10^{3} | 6{,}08 \times 10^{3} |
| Jason 3 | 7{,}70 \times 10^{3} | 6{,}74 \times 10^{3} |
Doc.
Cartographie de la température de surface des mers et de l'océan Atlantique
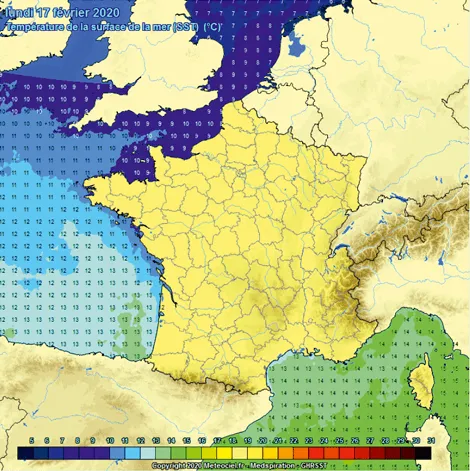
Le site propose quotidiennement une carte de température de la mer autour des côtes françaises.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADistance Terre‑Lune
✔ REA : Utiliser un modèle
On fait l'approximation, pour les calculs, que l'orbite de la Lune autour de la Terre peut être considérée comme circulaire.
1. En utilisant la deuxième loi de Newton, démontrer que la période de révolution de la Lune T et la distance Terre‑Lune D sont reliées par la formule : \dfrac{T^2}{D^3} = \dfrac{4 \ \pi^2}{G \cdot M_T}
2. En déduire la distance Terre‑Lune D.
3. Calculer l'écart relatif \epsilon entre les valeurs d'apogée et de périgée et conclure quant à l'approximation de l'orbite circulaire.
On fait l'approximation, pour les calculs, que l'orbite de la Lune autour de la Terre peut être considérée comme circulaire.
Données
- Période de révolution de la Lune : T = 656 h
- Masse de la Terre : M_T = 5{,}97 \times 10^{24} kg
- Constante de gravitation universelle : G = 6{,}67 \times 10^{-11} m3·kg-1·s-2
- Distance maximale entre la Terre et la Lune (apogée) : a = 406~300 km
- Distance minimale entre la Terre et la Lune (périgée) : b = 356~700 km
1. En utilisant la deuxième loi de Newton, démontrer que la période de révolution de la Lune T et la distance Terre‑Lune D sont reliées par la formule : \dfrac{T^2}{D^3} = \dfrac{4 \ \pi^2}{G \cdot M_T}
2. En déduire la distance Terre‑Lune D.
3. Calculer l'écart relatif \epsilon entre les valeurs d'apogée et de périgée et conclure quant à l'approximation de l'orbite circulaire.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
