Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 18
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41Triangles opposés par le sommet.
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
✔ J'extrais et j'exploite les informations utiles d'un document
✔ J'extrais et j'exploite les informations utiles d'un document
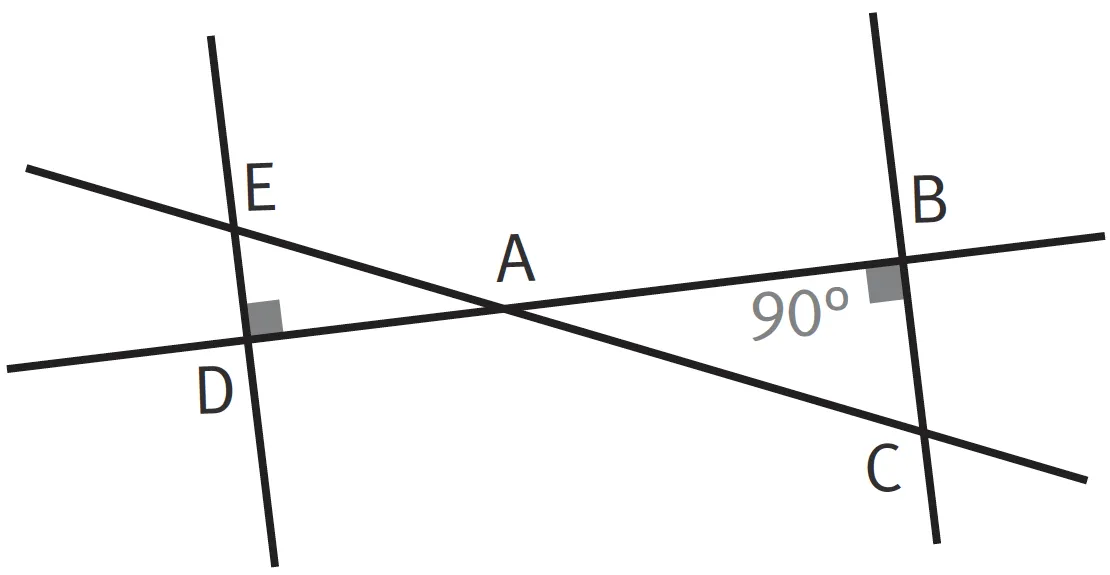
Dans ces triangles rectangles, DA = 5 cm, DE = 7 cm et AC = 4 cm.
Calculez les longueurs AB et BC (arrondies au mm).
Calculez les longueurs AB et BC (arrondies au mm).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Pour calculer des longueurs dans deux triangles opposés par le sommet, on peut utiliser la trigonométrie. Il faut avant cela justifier lʼégalité des deux angles qui ont le même sommet A et qui sont formés par deux droites.
Calcul de AB : \text{AB} = \dfrac{5\times 4}{\sqrt{74}} soit \text{AB} \approx 2\text{,}3
AB mesure environ 2,3 cm.
Calcul de BC : \text{BC} = \dfrac{7\times 4}{\sqrt{74}} soit \text{BC} \approx 3\text{,}3
BC mesure environ 3,3 cm.
Corrigé 1
- Comme les angles \widehat{\text{DAE}} et \widehat{\text{BAC}} sont égaux, on peut utiliser la trigonométrie pour calculer les longueurs demandées.
- Dans le triangle ADE rectangle en D, on applique le théorème de Pythagore :
AE2 = DA2 + DE2
AE2 = 52 + 72
AE2 = 25 + 49
AE2 = 74
- Suite à l'égalité des angles mentionnés, on obtient les égalités \cos(\widehat{\text{DAE}})=\cos(\widehat{\text{BAC}}) et \sin(\widehat{\text{DAE}})=\sin(\widehat{\text{BAC}}).
La première égalité donne \dfrac{\text{DA}}{\text{AE}} = \dfrac{\text{AB}}{\text{AC}} soit \text{AB}=\dfrac{\text{DA}\times\text{AC}}{\text{AE}}.
La seconde égalité donne \dfrac{\text{DE}}{\text{AE}} = \dfrac{\text{BC}}{\text{AC}} soit \text{BC}=\dfrac{\text{DE}\times\text{AC}}{\text{AE}}.
Calcul de AB : \text{AB} = \dfrac{5\times 4}{\sqrt{74}} soit \text{AB} \approx 2\text{,}3
AB mesure environ 2,3 cm.
Calcul de BC : \text{BC} = \dfrac{7\times 4}{\sqrt{74}} soit \text{BC} \approx 3\text{,}3
BC mesure environ 3,3 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Pour calculer des longueurs dans deux triangles opposés par le sommet, on peut appliquer le théorème de Thalès après avoir justifié le parallélisme des droites qui forment leurs bases respectives.
AB mesure environ 2,3 cm.
Calcul de BC : \text{BC} = \dfrac{28}{\sqrt{74}} soit \text{BC} \approx 3\text{,}3
BC mesure environ 3,3 cm.
Corrigé 2
- On sait que les droites (DE) et (BC) sont perpendiculaires à une même droite, (BD). Elles sont donc parallèles entre elles.
- Dans le triangle ADE rectangle en D, on applique le théorème de Pythagore :
AE2 = DA2 + DE2
AE2 = 52 + 72
AE2 = 25 + 49
AE2 = 74
- On sait que les droites (CE) et (BD) sont sécantes en A et que les droites (BC) et (DE) sont parallèles. Dʼaprès le théorème de Thalès :
\dfrac{\text{AB}}{\text{AD}} = \dfrac{\text{AC}}{\text{AE}} = \dfrac{\text{BC}}{\text{DE}}
\dfrac{\text{AB}}{5} = \dfrac{4}{\sqrt{74}} = \dfrac{\text{BC}}{7}
AB mesure environ 2,3 cm.
Calcul de BC : \text{BC} = \dfrac{28}{\sqrt{74}} soit \text{BC} \approx 3\text{,}3
BC mesure environ 3,3 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Problème similaireVoir p. 404 : Jouer au billard.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
