Chapitre 18
Exercices
Exercices numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67Logiciel de géométrie dynamiqueÀ la découverte des sinus, cosinus et tangente
Dans cet exercice, on va utiliser les outils de géométrie et dʼalgèbre pour vérifier les formules apprises en cours.

1. Reproduisez la figure avec le logiciel. On veut que la droite (BC) soit perpendiculaire au segment [AB]. Utilisez lʼoutil « angle » pour afficher les angles intérieurs du triangle.
2. Ouvrez le menu « algèbre ». Dans un premier temps, calculez les cosinus, sinus et tangente des angles \widehat{\text{BAC}} et \widehat{\text{ACB}}. Dans un second temps, calculez les rapports de longueurs \dfrac{\text{BC}}{\text{AC}}, \dfrac{\text{AB}}{\text{AC}}, \dfrac{\text{AB}}{\text{BC}} et \dfrac{\text{BC}}{\text{AB}}.
3. Comparez les rapports de longueurs aux valeurs des sinus, cosinus et tangente calculées plus haut. Que pouvez-vous constater concernant \cos {\widehat{\text{BAC}}} et \sin {\widehat{\text{ACB}}} ? Et \sin {\widehat{\text{BAC}}} et \cos {\widehat{\text{ACB}}} ?
4. Enfin, en faisant varier la position des points, et donc la valeur des angles, que constatez-vous ? Quel point est-il utile de déplacer ?

1. Reproduisez la figure avec le logiciel. On veut que la droite (BC) soit perpendiculaire au segment [AB]. Utilisez lʼoutil « angle » pour afficher les angles intérieurs du triangle.
2. Ouvrez le menu « algèbre ». Dans un premier temps, calculez les cosinus, sinus et tangente des angles \widehat{\text{BAC}} et \widehat{\text{ACB}}. Dans un second temps, calculez les rapports de longueurs \dfrac{\text{BC}}{\text{AC}}, \dfrac{\text{AB}}{\text{AC}}, \dfrac{\text{AB}}{\text{BC}} et \dfrac{\text{BC}}{\text{AB}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68TableurFonctions trigonométriques du tableur
Dans cet exercice, on connait un angle et on va utiliser le tableur pour calculer des longueurs à lʼaide de cet angle.

3. En utilisant un logiciel de géométrie dynamique, tracez un triangle rectangle dont vous afficherez les longueurs et les angles intérieurs. Donnez à votre voisin la valeur dʼun des angles, la valeur dʼun des côtés, et demandez-lui de trouver la valeur dʼun des côtés manquants. Vérifiez quʼil obtient bien la bonne valeur grâce au tableur. Échangez les rôles.


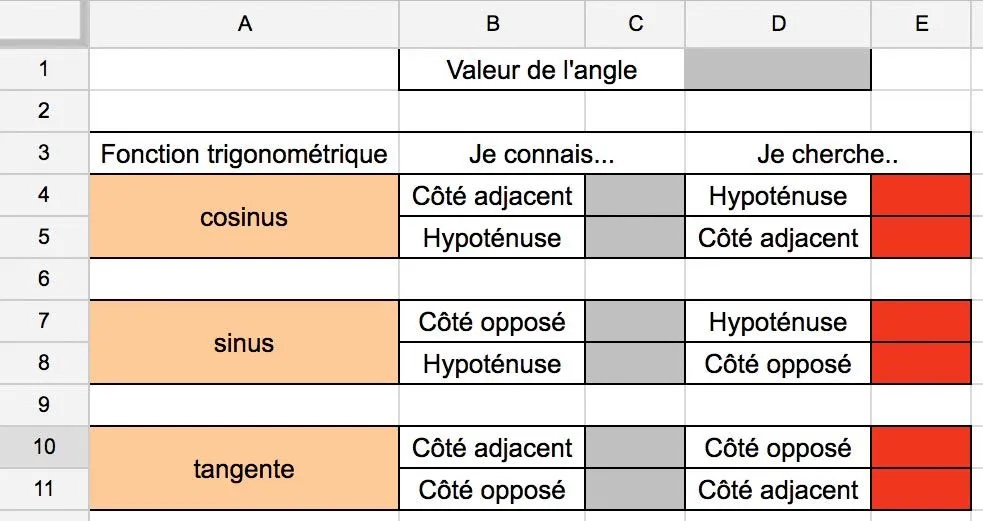
1. Ouvrez le tableur et complétez les cases orangées avec les fonctions trigonométriques appropriées.
2. Complétez les cellules rouges avec les formules appropriées pour que le résultat du calcul soit la valeur de la longueur cherchée. Les cellules grises accueilleront les valeurs supposées connues. On utilisera les fonctions COS(RADIANS( )), SIN((RADIANS( )) et TAN(RADIANS( )) pour représenter respectivement le cosinus, le sinus et la tangente dʼun angle exprimé en degrés.
2. Complétez les cellules rouges avec les formules appropriées pour que le résultat du calcul soit la valeur de la longueur cherchée. Les cellules grises accueilleront les valeurs supposées connues. On utilisera les fonctions COS(RADIANS( )), SIN((RADIANS( )) et TAN(RADIANS( )) pour représenter respectivement le cosinus, le sinus et la tangente dʼun angle exprimé en degrés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
En mathématiques, il est possible dʼexprimer un angle dans différentes unités, comme pour les longueurs, qui peuvent être exprimées par exemple en mètres ou en pieds (mesure anglo-saxonne). Pour les angles, les deux unités principales sont les degrés et les radians.
Lʼunité la plus pratique à utiliser pour les mathématiciens est le radian. Néanmoins, dans la classe de collège, la plus simple est le degré. Les fonctions cosinus, sinus, tangente et leurs réciproques sont utilisées par rapport aux radians dans le tableur, il faut donc dʼabord convertir les radians en degrés pour travailler.
Voilà pourquoi on utilise la fonction RADIANS() dans lʼexercice précédent.
Lʼunité la plus pratique à utiliser pour les mathématiciens est le radian. Néanmoins, dans la classe de collège, la plus simple est le degré. Les fonctions cosinus, sinus, tangente et leurs réciproques sont utilisées par rapport aux radians dans le tableur, il faut donc dʼabord convertir les radians en degrés pour travailler.
Voilà pourquoi on utilise la fonction RADIANS() dans lʼexercice précédent.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

