Mathématiques 3e - 2021
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Partie 1 : Nombres et calculs
Ch. 1
Nombres entiers
Ch. 2
Calcul numérique
Ch. 3
Calcul littéral
Ch. 4
Équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 5
Notion de fonction
Ch. 6
Fonctions affines
Ch. 7
Situations de proportionnalité
Ch. 8
Statistiques
Ch. 9
Probabilités
Partie 3 : Espace et géométrie
Ch. 10
Théorème de Thalès et triangles semblables
Ch. 11
Trigonométrie dans le triangle rectangle
Ch. 12
Transformations dans le plan et leurs effets
Ch. 13
Géométrie dans l'espace
Partie 4 : Mesures et grandeurs
Ch. 14
Mesures et grandeurs
Annexes
Scratch
Dossier brevet
Rappels, Index, Compétences
Révisions Genially
Calcul littéral
Plan de travail
Chapitre 10
Activités
Découvrir le chapitre : Théorème de Thalès et triangles semblables
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Des rapports de longueurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
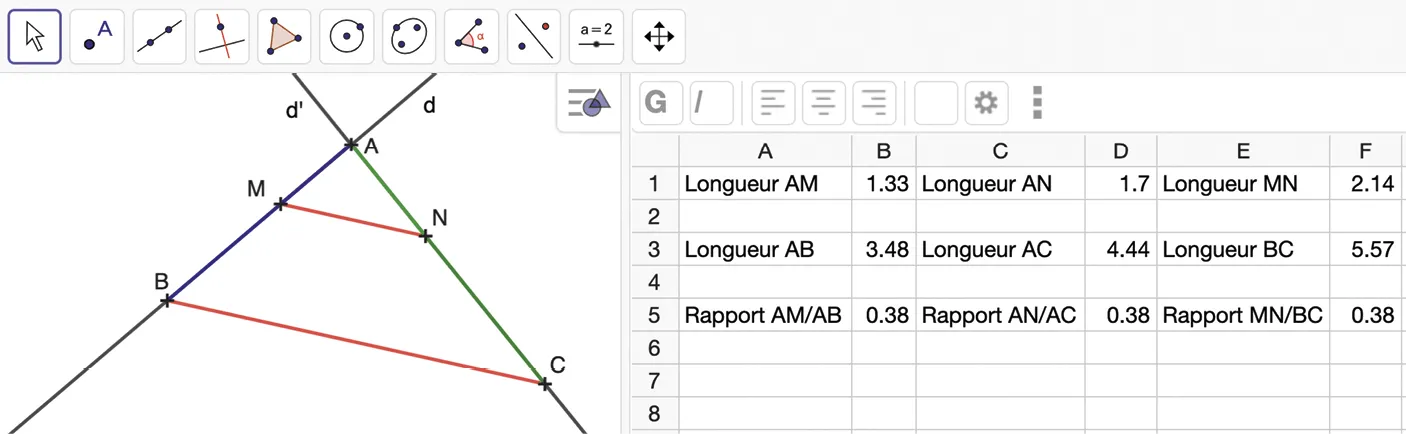
Soient deux droites (d) et (d') sécantes en \text{A} et deux points \text{B} et \text{C} tels que \mathrm{B} \in(d) et \mathrm{C} \in\left(d^{\prime}\right). Dans le triangle \text{ABC}, on place un point \text{M} appartenant à [\mathrm{AB}] et un point \text{N} appartenant à [\mathrm{AC}] tels que les droites (\mathrm{MN}) et (\mathrm{BC}) soient parallèles.
Télécharger le fichier .
GeoGebra
1
a)
Quelles informations figurent dans les lignes 1, 3 et 5 du tableur ?
b) Après avoir déplacé les points \text{M} et \text{N}, quelle constatation peut‑on faire à propos des valeurs apparaissant dans la ligne 5 du tableur ?
c) Quel théorème permet de justifier cette constatation ?
2
On déplace ensuite les points \text{M} et \text{N} de telle sorte que ceux‑ci appartiennent respectivement aux demi‑droites [\mathrm{AB}) et [\mathrm{AC}) mais pas aux segments [\mathrm{AB}] et [\mathrm{AC}]. Que remarque‑t‑on pour les valeurs de la ligne 5 ?
3
Enfin, on déplace les points \text{M} et \text{N} de telle sorte que ceux‑ci n'appartiennent pas aux demi‑droites [\mathrm{AB}) et [\mathrm{AC}). Que remarque‑t‑on pour les valeurs de la ligne 5 ?
Bilan
Énoncer le théorème de Thalès dans le cas général.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2L'importance de la position des points
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Que valent les quotients \frac{\mathrm{AM}}{\mathrm{AB}} et \frac{\mathrm{AN}}{\mathrm{AC}} dans la figure ci‑contre ? Que peut‑on conjecturer sur la position des droites (\mathrm{MN}) et (\mathrm{BC}) ?
2
Que valent les quotients \frac{\mathrm{AP}}{\mathrm{AB}} et \frac{\mathrm{AN}}{\mathrm{AC}} ? Que peut‑on conjecturer sur la position des droites (\mathrm{PN}) et (\mathrm{BC}) ?
Bilan
Quelle condition les points doivent‑ils vérifier pour que les droites soient parallèles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3Agrandissement et réduction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
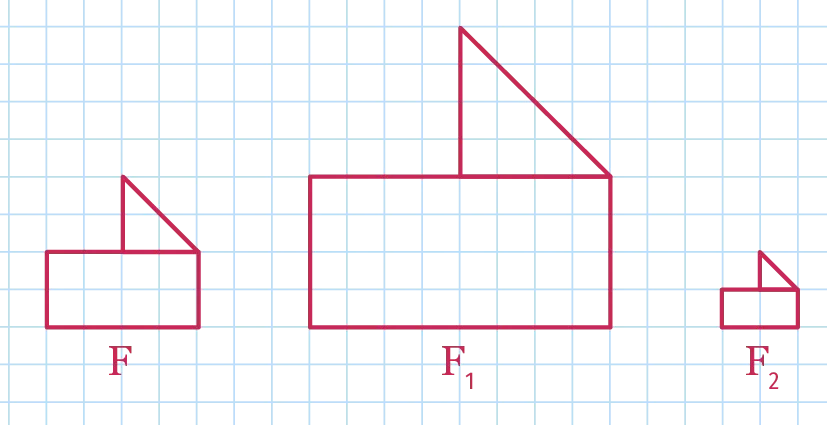
On considère les figures \text{F}, \text{F}_1 et \text{F}_2 suivantes.
1
Compléter la phrase ci‑dessous avec les propositions suivantes :
« La figure \text{F}_1 est de la figure \text{F}, car les longueurs sont multipliées par ; la figure \text{F}_2 est de la figure \text{F}, car les longueurs sont multipliées par .
2
En choisissant le carreau comme unité d'aire, donner les aires \text{A}, \text{A}_1 et \text{A}_2 des figures \text{F}, \text{F}_1 et \text{F}_2 et compléter les égalités : \mathrm{A}_{1}=Bilan
Énoncer la conséquence d'un agrandissement ou d'une réduction sur les aires.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 4Un triangle, trois angles et des longueurs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Tracer un triangle \text{ABC} tel que \widehat{\mathrm{BAC}}=40^{\circ}, \widehat{\mathrm{ABC}}=60^{\circ} et \widehat{\mathrm{ACB}}=80^{\circ}. Comparer cette figure avec celle de vos voisins. Tous les triangles sont‑ils identiques ?
GeoGebra
2
Le professeur a reporté les mesures des côtés des triangles de certains des élèves de la classe dans le tableau ci‑dessous.
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| \bm{\text{AB}} | 8 | 12 | 4 | 20 | 16 |
| \bm{\text{AC}} | 7 | 10,5 | 3,5 | 17,5 | 14 |
| \bm{\text{BC}} | 5,2 | 7,8 | 2,6 | 13 | 10,4 |
Comparer les mesures des côtés des triangles 2 ; 3 ; 4 et 5 avec celles du triangle 1.
Coup de pouce
Penser à calculer le rapport entre les longueurs respectives des côtés des triangles.
3
On dit que ces triangles sont semblables. Donner les longueurs d'un nouveau triangle semblable aux précédents.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
