Partie 4
Histoire des mathématiques
Dérivation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Naissance du calcul différentiel
Au début du XVIIe siècle, des scientifiques tels que Galilée ou Kepler sont amenés à étudier des courbes dans diverses situations : orbites des planètes, trajectoire d'un projectile, etc. Afin de résoudre un certain nombre de problèmes comme par exemple prédire des trajectoires, il est plus simple pour ces savants d'étudier des portions de courbes infiniment petites. Les quantités étudiées dans ce cas sont qualifiées d'infinitésimales.
C'est d'abord Cavalieri (1598-1647), notamment, qui cherche à théoriser cette notion d'infiniment petit. Il s'appuie sur les travaux d'Archimède et développe ensuite son propre concept d'indivisibles permettant de calculer des aires et des volumes. Ses idées séduisent et se généralisent, mais la conception de ces infiniment petits reste encore difficile à maîtriser.
À la fin du XVIIe siècle, indépendamment l'un de l'autre, les travaux de Newton (1642-1727) et Leibniz (1646-1716) vont jeter les bases du calcul infinitésimal qui sera exploitable et dans de très nombreux domaines.

Gottfried Wilhelm Leibniz (1646‐1716)


Isaac Newton (1642‐1727)

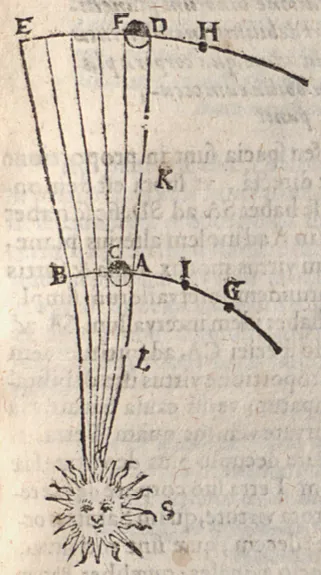
Image du système solaire présenté par Kepler.
C'est d'abord Cavalieri (1598-1647), notamment, qui cherche à théoriser cette notion d'infiniment petit. Il s'appuie sur les travaux d'Archimède et développe ensuite son propre concept d'indivisibles permettant de calculer des aires et des volumes. Ses idées séduisent et se généralisent, mais la conception de ces infiniment petits reste encore difficile à maîtriser.
À la fin du XVIIe siècle, indépendamment l'un de l'autre, les travaux de Newton (1642-1727) et Leibniz (1646-1716) vont jeter les bases du calcul infinitésimal qui sera exploitable et dans de très nombreux domaines.

Gottfried Wilhelm Leibniz (1646‐1716)


Isaac Newton (1642‐1727)


Image du système solaire présenté par Kepler.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les principes de Newton et de Leibniz
Les travaux de Newton et de Leibniz sont sensiblement similaires.
Il s'agit de déterminer une valeur approchée de la longueur de l'arc de courbe entre \mathrm{M} et \mathrm{M}^{\prime} en utilisant le triangle \mathrm{MAB} ci-contre rectangle en \mathrm{A}, où (\mathrm{MB}) est la tangente à la courbe en \mathrm{M}.

Newton, célèbre pour sa théorie de la gravitation universelle, publie
tardivement ses travaux sur le sujet en 1671 dans Tractatus de Methodis
Serierum et Fluxionum. L'influence de la physique y est omniprésente.
Il considère un objet se déplaçant du point \mathrm{M} au point \mathrm{M}^{\prime} en un temps
infinitésimal qu'il note o. Les vitesses horizontale et verticale de cet
objet théorique sont respectivement notées \dot{x} et \dot{y}. Il peut alors écrire, dans le triangle ci-dessus, a=\dot{xo} et b=\dot{yo}. Il effectue ses calculs en considérant que certaines valeurs peuvent être négligées puisque le temps o considéré est infinitésimal. Cette démarche lui permet d'aboutir à une approximation valide de la longueur d'arc recherchée.


Extrait de Tractatus de Methodis Serierum et Fluxionum de Newton.
Leibniz ne connaît pas les travaux de Newton mais trouve que les méthodes de ses contemporains sont trop compliquées et cherche à les simplifier. En 1684, il écrit un mémoire où il introduit ses idées : Nova Methodus pro Maximis et Minimis, itemque Tangentibus..., & Singulare pro illis Calculi Genus.
\mathrm{} Il note a = \mathrm{d}x, b = \mathrm{d}y et c = \mathrm{d}s les longueurs du triangle \mathrm{MAB} précédent qu'il appelle triangle caractéristique infinitésimal. Il utilise le théorème de Pythagore et simplifie ses calculs en expliquant lui aussi que certaines valeurs peuvent être considérées comme négligeables.
\mathrm{} Il note a = \mathrm{d}x, b = \mathrm{d}y et c = \mathrm{d}s les longueurs du triangle \mathrm{MAB} précédent qu'il appelle triangle caractéristique infinitésimal. Il utilise le théorème de Pythagore et simplifie ses calculs en expliquant lui aussi que certaines valeurs peuvent être considérées comme négligeables.


Nova Methodus pro Maximis et Minimis de Leibniz.
Les frères Jacques (1654-1705) et Jean Bernoulli (1667-1748) sont immédiatement séduits par les calculs de Leibniz. Ils les reprennent et les utilisent abondamment pour obtenir bon nombre de nouveaux résultats mathématiques. Cette utilisation des méthodes de Leibniz assure une rapide diffusion du calcul infinitésimal. Plus tard, la dérivée d'une fonction f parrapport à sa variable x sera notée \frac{\mathrm{d} f}{\mathrm{~d} x}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Naissance de la fonction exponentielle
On sait depuis longtemps calculer des puissances entières comme 3^{4}=3 \times 3 \times 3 \times 3. Mais quelle signification pourrait-on donner à des puissances irrationnelles comme par exemple 3^{\sqrt{2}} ? La réponse rigoureuse à ce besoin n'a pu se faire qu'avec le développement du calcul différentiel, la formalisation de la notion de fonction et la construction de la fonction logarithme. Nous voici donc entre la fin du XVIIe siècle et le début du XVIIIe.
Dans une lettre de 1690 de Leibniz à Huygens (1629-1695), on trouve la première définition de la base naturelle des logarithmes, nombre qui sera plus tard noté e. En 1690, Jacques Bernoulli étudie le problème des taux d'intérêt composés continus et, en 1694, les échanges entre Jean Bernoulli et Leibniz permettent de mieux définir la fonction exponentielle. Dans son Principia Calculi Exponentialium seu Percurrentium publié en 1697, Jean Bernoulli étudie complètement la fonction exponentielle. C'est à Leonhard Euler (1707-1783) que l'on doit la première utilisation de la lettre \mathrm{e} comme notation pour la base du logarithme naturel (1728) et comme notation pour l'exponentielle. En 1778, il démontre que e est un nombre irrationnel et il en donne une valeur approchée à 23 décimales. Il faudra enfin attendre 1874 et les travaux de Charles Hermite (1822-1901) pour prouver que le nombre \mathrm{e} est transcendant, c'est-à-dire qu'il ne peut pas être solution d'une équation algébrique.
Dans une lettre de 1690 de Leibniz à Huygens (1629-1695), on trouve la première définition de la base naturelle des logarithmes, nombre qui sera plus tard noté e. En 1690, Jacques Bernoulli étudie le problème des taux d'intérêt composés continus et, en 1694, les échanges entre Jean Bernoulli et Leibniz permettent de mieux définir la fonction exponentielle. Dans son Principia Calculi Exponentialium seu Percurrentium publié en 1697, Jean Bernoulli étudie complètement la fonction exponentielle. C'est à Leonhard Euler (1707-1783) que l'on doit la première utilisation de la lettre \mathrm{e} comme notation pour la base du logarithme naturel (1728) et comme notation pour l'exponentielle. En 1778, il démontre que e est un nombre irrationnel et il en donne une valeur approchée à 23 décimales. Il faudra enfin attendre 1874 et les travaux de Charles Hermite (1822-1901) pour prouver que le nombre \mathrm{e} est transcendant, c'est-à-dire qu'il ne peut pas être solution d'une équation algébrique.


Christian Huygens (1629‐1695)


Leonhard Euler (1707‐1783)
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

