Émission et perception d'un son

Un son est créé par la vibration rapide d'un objet comme les cordes d'une guitare (doc. 1), les ailes d'un insecte ou les feuilles d'un arbre au vent.

Cette vibration est souvent d'amplitude micrométrique à millimétrique et provoque des sons de faible intensité. Pour résoudre ce problème, beaucoup d'instruments (doc. 2) et d'êtres vivants sont dotés d'une caisse de résonance.

Une caisse de résonance amplifie et sélectionne les sons.

La corde vibre quand elle est pincée.

On entend un son en étant à distance de la source qui l'a créé : entre la source sonore et l'oreille, il y a propagation du son.

La vibration initiale est transmise de proche en proche au niveau microscopique (entre molécules ou entre atomes), sans que l'objet qui vibre ne se déplace lui-même. Comme une ola dans un stade : la vague se déplace, mais les supporters ne l'accompagnent pas dans son déplacement latéral.

On parle de signal sonore qui se propage depuis la source.

Un signal sonore est un phénomène de déplacement d'une perturbation de proche en proche dans un milieu matériel et sans transport effectif de matière.

L'onde sonore nécessite un milieu de propagation pour se déplacer : ce milieu peut être l'air, le bois, le métal, l'eau ou tout autre matériau. En l'absence de milieu matériel (c'est-à-dire le vide), il ne peut y avoir propagation du son. Ainsi, sur la Lune qui n'a pas d'atmosphère, les sons ne se propagent pas.

• La vibration de l'objet qui crée le son n'est pas forcément visible à l'œil nu ; elle peut être microscopique et en général bien trop rapide pour l'œil.
• Ne pas confondre résonner (augmenter l'intensité sonore) et raisonner (réfléchir, penser).

Dans un milieu donné, le son se propage avec une vitesse caractéristique. Cette vitesse, appelée aussi célérité, dépend de la nature du milieu et de la température. Dans l'air, vers 20 °C, la célérité du son est voisine de 340 m\cdots^-1.

Dans le vide, le son ne peut se propager parce qu'il n'y a pas de matière. L'onde sonore ne peut exister.

• Célérité : vitesse de propagation d'une onde, à distinguer de la vitesse d'un corps matériel. En effet, pour une onde, il n'y a aucun déplacement de matière.

À l'aide d'un microphone, on peut transformer un signal sonore en signal électrique. Ce signal converti est alors visualisable sur un oscilloscope ou sur un ordinateur, sous la forme d'un graphique (voir doc. 4).

Les tensions observées sont proportionnelles à l'intensité de l'onde sonore.

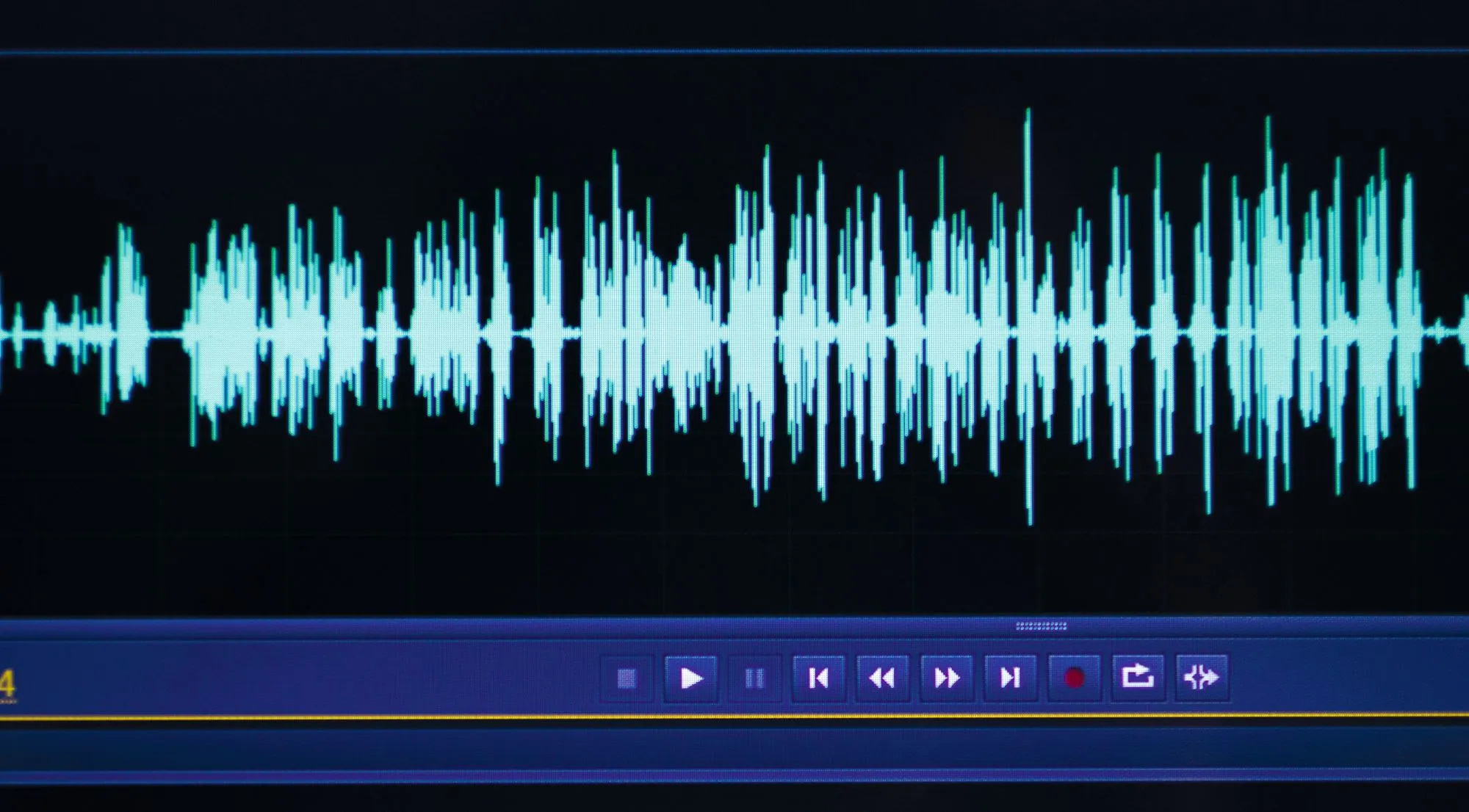
Un son transformé en signal électrique et visualisé dans un logiciel de musique.

Le signal observé permet d'analyser ce son. On peut constater que ce signal est périodique sur une durée plus ou moins longue, c'est-à-dire qu'il se reproduit identique à lui-même (doc. 5) à un intervalle de temps régulier appelé période.

La période d'un signal périodique se lit sur un graphique qui représente le signal lorsque le temps est en abscisse.

C'est la durée du plus court « motif  » qui se répète identique à lui-même. La période s'exprime en seconde (s).

La fréquence f du son représente le nombre de périodes de ce signal par seconde. Elle se calcule par f=\dfrac{1}{T}.

Elle s'exprime en hertz (Hz) si T est en seconde (s).

• La période T est parfois exprimée en millisecondes (ms). Pour déterminer la fréquence f, il faut convertir la valeur de T en secondes (s) pour obtenir un résultat de la fréquence en hertz (Hz).

Un son de fréquence élevée donne un son aigu, une fréquence basse donne un son grave.

C'est la fréquence qui définit la hauteur d'un son.

En musique, des sons de même hauteur représentent la même note (par exemple un La3 si la fréquence est de 440 Hz).

Pourtant, même si deux instruments jouent la même note, ils sont différentiables et identifiables à l'oreille. Leur timbre est différent (doc. 6).

Le timbre d'un son (et par extension, le timbre d'un instrument de musique) est l'ensemble des caractéristiques du signal permettant de distinguer ce son d'un autre son de même hauteur.

Ibrahim Maalouf en concert, 2014.

L'oreille humaine ne perçoit que certaines fréquences sonores. Un son trop grave ou trop aigu ne sera pas entendu.

Le domaine de fréquences des sons audibles est compris entre 20 Hz et 20 kHz (doc. 8).

Ces valeurs peuvent varier d'un individu à l'autre et le domaine de fréquences audibles se réduit avec l'âge.
En deçà de 20 Hz, on se situe dans le domaine des infrasons.
Au-delà de 20 kHz, il s'agit d'ultrasons.

Remarque : Des sons de fréquences non audibles pour l'humain le sont pour certains animaux. Certains capteurs microphoniques particuliers sont adaptés pour capter ces fréquences inaudibles à notre oreille.

Les infrasons, les ultrasons et les sons audibles par les humains.

Un son est deux fois plus intense si la source sonore vibre avec une amplitude deux fois plus grande (doc. 9). Pourtant, il ne sera pas perçu deux fois plus fort par l'oreille.
L'oreille ne réagit donc pas proportionnellement à l'intensité I de l'onde sonore.

Pour modéliser cette réalité, on définit le niveau d'intensité sonore L, exprimé en décibel (dB), qui n'est pas proportionnel à l'amplitude.

On peut mesurer le niveau d'intensité sonore grâce à un sonomètre (doc. 10).

• La hauteur du signal électrique sur le graphique s'appelle l'amplitude du signal.
• La hauteur d'un son (son grave ou aigu) dépend de la période ou de la fréquence du signal associé. Cette notion ne doit surtout pas être confondue avec l'amplitude !

L'onde sonore peut représenter un danger pour l'oreille, si son niveau d'intensité sonore est trop élevé. Le niveau 0 dB est le niveau en dessous duquel une oreille moyenne ne détectera pas le son.

On définit une échelle de niveau sonore qui précise les conséquences de l'exposition de l'oreille à des sons de différentes intensités. Au-delà d'un certain niveau, la vibration peut endommager l'oreille irrémédiablement.

Outil servant à mesurer le niveau sonore.