Chapitre 6
J'apprends
Proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
AReconnaitre une situation de proportionnalité
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Notion de proportionnalité
Définition
Deux grandeurs sont proportionnelles si on peut obtenir toutes les valeurs de lʼune en multipliant celles de lʼautre par un même nombre non nul. Ce nombre est appelé coefficient de proportionnalité.
Exercices n° p. 130-131.
J'applique
Consigne :
Parmi les couples de grandeurs suivantes, lesquelles sont proportionnelles ?
a. La température d'un réfrigérateur et la distance Terre-Lune.
b. La masse de tomates dans un sachet et le prix du sachet.
c. La puissance d'une voiture et le nombre de ses vitres.
d. L'âge d'une personne et sa taille.
Correction :
a. Il n'y a pas proportionnalité.
b. Plus vous achetez de grammes de tomates, plus vous payez, il y a donc proportionnalité.
c. Il n'y a pas proportionnalité.
d. Il n'y a pas proportionnalité, car on arrête de grandir à l'âge adulte.
Aide
Deux grandeurs peuvent être liées mais pas proportionnelles : lʼâge et la taille en sont un exemple.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Représentation
Définition
Un tableau qui donne plusieurs valeurs prises par 2 grandeurs proportionnelles est un tableau de proportionnalité.
Exercices n° p. 130-131.
Exemples :
Au supermarché, le prix des tomates est proportionnel à la masse achetée. On peut donc présenter les grandeurs dans un tableau de proportionnalité. On passe dʼune valeur à lʼautre en multipliant ou divisant par 2,5.
2,5 est donc le coefficient de proportionnalité.


Propriété
Lorsquʼon représente graphiquement deux grandeurs proportionnelles, on obtient des points alignés sur une droite passant par lʼorigine du repère.
Exercices n° p. 134.
J'applique
Consigne :
Parmi les graphiques suivants, lequel décrit une situation de proportionnalité ?
a.
 b.
b.
 c.
c.

Correction :



Le graphique c. représente une situation de proportionnalité car ses points sont alignés avec l'origine du repère.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BCompléter un tableau de proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je découvre
Méthode
Utiliser le coefficient multiplicateur
Voici un tableau de proportionnalité à compléter.
 Pour trouver le coefficient multiplicateur, il faut choisir deux valeurs connues et proportionnelles, puis diviser lʼune par lʼautre. Il ne reste quʼà sʼen servir pour compléter les cases vides.
Pour trouver le coefficient multiplicateur, il faut choisir deux valeurs connues et proportionnelles, puis diviser lʼune par lʼautre. Il ne reste quʼà sʼen servir pour compléter les cases vides.

Voici un tableau de proportionnalité à compléter.


Exercices n° p. 131-132.
ligne pour que le coefficient multiplicateur soit supérieur à 1.
Méthode
On peut additionner ou soustraire des colonnes dʼun tableau de proportionnalité pour en obtenir une nouvelle colonne.
On peut multiplier ou diviser une colonne dʼun tableau de proportionnalité par un nombre non nul pour en obtenir une nouvelle colonne.

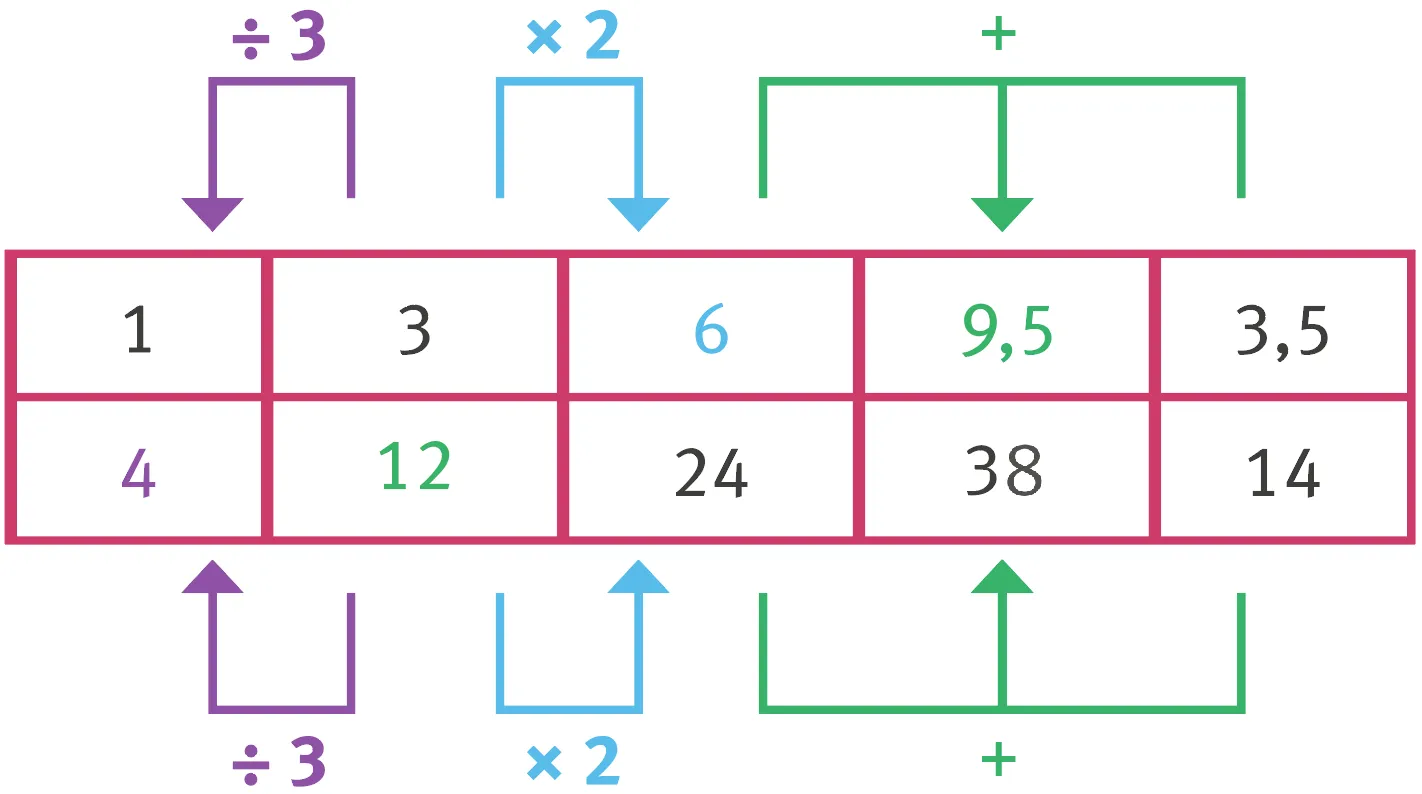
On peut multiplier ou diviser une colonne dʼun tableau de proportionnalité par un nombre non nul pour en obtenir une nouvelle colonne.


Exercices n° p. 131-132.
J'approfondis
Méthode
Quand on a trois données a, b, c dans un tableau de proportionnalité, on peut calculer la valeur x dans la quatrième case à lʼaide de lʼégalité du produit en croix.
La valeur x est appelée quatrième proportionnelle.
 Par proportionnalité, \dfrac{\color{#3ab4e0}a}{\color{#ab4657}b} = \dfrac{\color{#ab4657}c}{\color{#3ab4e0}x} donc {\color{#ab4657}c} \times {\color{#ab4657}b} = {\color{#3ab4e0}a} \times \color{#3ab4e0}x. On a donc {\color{#3ab4e0}x} =~\dfrac{{\color{#ab4657}c} \times \color{#ab4657}b}{\color{#3ab4e0}a}.
Par proportionnalité, \dfrac{\color{#3ab4e0}a}{\color{#ab4657}b} = \dfrac{\color{#ab4657}c}{\color{#3ab4e0}x} donc {\color{#ab4657}c} \times {\color{#ab4657}b} = {\color{#3ab4e0}a} \times \color{#3ab4e0}x. On a donc {\color{#3ab4e0}x} =~\dfrac{{\color{#ab4657}c} \times \color{#ab4657}b}{\color{#3ab4e0}a}.
La valeur x est appelée quatrième proportionnelle.

Exercices n° p. 134-135.
J'applique
Consigne :
Le tableau suivant représente une situation de proportionnalité. Trouvez la valeur de x.

Le tableau suivant représente une situation de proportionnalité. Trouvez la valeur de x.

Correction :
D'après l'égalité des produits en croix, on a :
{\color{#c21546}9} \times {\color{#c21546}5} = {\color{#3ab4e0}4} \times \color{#3ab4e0}x
Donc {\color{#3ab4e0}x} = \dfrac{{\color{#c21546}9} \times {\color{#c21546}5}}{\color{#3ab4e0}4}
{\color{#3ab4e0}x} = 11\text{,}25
D'après l'égalité des produits en croix, on a :
{\color{#c21546}9} \times {\color{#c21546}5} = {\color{#3ab4e0}4} \times \color{#3ab4e0}x
Donc {\color{#3ab4e0}x} = \dfrac{{\color{#c21546}9} \times {\color{#c21546}5}}{\color{#3ab4e0}4}
{\color{#3ab4e0}x} = 11\text{,}25
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CUtiliser les pourcentages
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je découvre
Rappel
Un pourcentage est une fraction dont le dénominateur vaut 100.
On peut exprimer une fraction en un pourcentage à lʼaide dʼun tableau de proportionnalité.
Voici deux méthodes pour trouver x :
On peut exprimer une fraction en un pourcentage à lʼaide dʼun tableau de proportionnalité.
Voici deux méthodes pour trouver x :
- On voit que 25 {\color{#3ca69b}\times 4} = 100 donc, comme cʼest un tableau de proportionnalité, 7 {\color{#3ca69b}\times 4} = x donc x = 28.
- On utilise lʼégalité des produits en croix. x =~\dfrac{7 \times 100}{25} = 28

Exercices n° p. 132-133.
J'approfondis
Propriété
Pour augmenter un nombre dʼun pourcentage p, on le multiplie par (1 + p).
Pour diminuer un nombre dʼun pourcentage p, on le multiplie par (1 -~p).
Pour diminuer un nombre dʼun pourcentage p, on le multiplie par (1 -~p).
Exercices n° p. 133 .
J'applique
Consigne :
Lors des soldes, une paire de chaussures voit son prix de 80 € baisser de 25 %. Quel est le nouveau prix de ces chaussures ?
Lors des soldes, une paire de chaussures voit son prix de 80 € baisser de 25 %. Quel est le nouveau prix de ces chaussures ?
Correction :
80 \times \left(1 - \dfrac{25}{100}\right) = 80 \times \dfrac{75}{100} = 60
Le nouveau prix est de 60 €.
80 \times \left(1 - \dfrac{25}{100}\right) = 80 \times \dfrac{75}{100} = 60
Le nouveau prix est de 60 €.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
DUtiliser les échelles
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Définition
On appelle échelle le coefficient multiplicateur entre la mesure de la représentation dʼun objet et sa mesure réelle, exprimées dans les mêmes unités.
Lʼéchelle est donnée par la formule :
Lʼéchelle est donnée par la formule :
\dfrac{\text{Dimension apparente}}{\text{Dimension réelle}}
Exercices n° p. 133.
J'applique
Consigne :
Une maquette de 30 cm de la Tour Eiffel a été construite. La véritable Tour Eiffel mesure 324 m. Quelle est lʼéchelle de la reproduction ?
Une maquette de 30 cm de la Tour Eiffel a été construite. La véritable Tour Eiffel mesure 324 m. Quelle est lʼéchelle de la reproduction ?
Correction :
324 m = 32 400 cm. Donc l'échelle de la reproduction est de \dfrac{30}{32\:400} =~\dfrac{1}{1\:080}.
On dit que la reproduction est au \text{1/1 080}e.
324 m = 32 400 cm. Donc l'échelle de la reproduction est de \dfrac{30}{32\:400} =~\dfrac{1}{1\:080}.
On dit que la reproduction est au \text{1/1 080}e.
Méthode
Un tableau de proportionnalité peut permettre de faire facilement correspondre des mesures réelles et apparentes.
Voici un tableau de proportionnalité lié à une carte à lʼéchelle 1/400 \: 000^e.

Voici un tableau de proportionnalité lié à une carte à lʼéchelle 1/400 \: 000^e.

Exercices n° p. 134.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


