Chapitre 6
Exercices
Exercices numériques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83Logiciel de géométrie dynamique, Tableur Angle et longueur d'arc de cercle
Nous allons utiliser un logiciel de géométrie dynamique pour étudier des propriétés géométriques du cercle et de lʼarc de cercle.
1. a. Construisez un arc de cercle dont on peut modifier lʼangle entre les deux segments qui relient le centre du cercle et les bords de lʼarc de cercle.
b. Si lʼangle \alpha vaut 0^{\circ}, quelle est la longueur de lʼarc ?
c. Si lʼangle α vaut 360^{\circ}, quelle est la longueur de lʼarc ?
d. Faites varier lʼangle \alpha, puis justifiez cette affirmation : « Il existe une relation de proportionnalité entre lʼarc de cercle et lʼangle qui le forme. »
2. a. Dans un fichier tableur, entrez les valeurs de la longueur de lʼarc d (colonne A) et de lʼangle \alpha (colonne B).
b. Calculez \dfrac{d}{\alpha} dans la cellule C1 du tableur, puis étirez la formule sur toute la colonne C.
c. Pourquoi ces quotients corroborent-t-ils lʼaffirmation : « Il existe une relation de proportionnalité entre lʼarc de cercle et lʼangle qui le forme. » ?
d. Quel est le coefficient de proportionnalité reliant la longueur de lʼarc et lʼangle qui le forme ?
e. Complètez les égalités suivantes : Si L est la longueur de lʼarc de cercle de rayon r formé par un angle \alpha, alors \dfrac{L}{...} = ... ; L = ... \times ... ; \alpha = \dfrac{...}{...}
1. a. Construisez un arc de cercle dont on peut modifier lʼangle entre les deux segments qui relient le centre du cercle et les bords de lʼarc de cercle.
Cliquez pour accéder à une zone de dessin
b. Si lʼangle \alpha vaut 0^{\circ}, quelle est la longueur de lʼarc ?
c. Si lʼangle α vaut 360^{\circ}, quelle est la longueur de lʼarc ?
b. Calculez \dfrac{d}{\alpha} dans la cellule C1 du tableur, puis étirez la formule sur toute la colonne C.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84TableurQuatrième proportionnelle
Nous allons calculer la quatrième proportionnelle à lʼaide dʼun tableur. Dans un tableur, recopiez le tableau suivant.

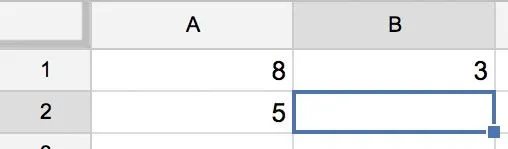
1. Dans la case B2, insérez une formule permettant de calculer le nombre qui fait de ce tableau un tableau de proportionnalité.
2. Dans la colonne A, ajoutez les nombres 3 et 1, puis copiez la formule de la cellule B2 dans B3 et B4.
a. Le tableau obtenu est-il un tableau de proportionnalité ?
b. Étudiez les formules des cases B3 et B4 : font-elles références aux cases A1, B2 et A2 ? Pourquoi cela nʼa-t-il pas de conséquences sur la nature du tableau ?
3. Listez toutes les formules qui permettent de compléter le tableau de proportionnalité suivant :

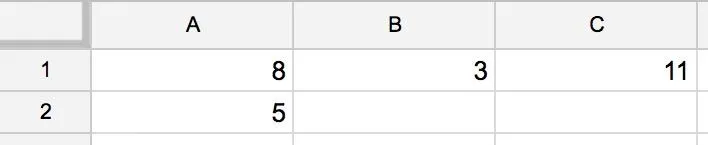


1. Dans la case B2, insérez une formule permettant de calculer le nombre qui fait de ce tableau un tableau de proportionnalité.
a. Le tableau obtenu est-il un tableau de proportionnalité ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85Logiciel de géométrie dynamiqueTrajets à Marseille
Deux familles passeront leurs vacances à Marseille. L'une part de Reims, l'autre de Strasbourg. Elles se rejoindront aux alentours de Lyon et termineront la route ensemble.Téléchargez le fichier ressource de l'exercice.
À l'aide du fichier ressource de l'exercice, déterminez si les deux familles parcourront plus ou moins du tiers de leur trajet ensemble.
À l'aide du fichier ressource de l'exercice, déterminez si les deux familles parcourront plus ou moins du tiers de leur trajet ensemble.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exercice numérique
On considère le programme de calcul suivant :

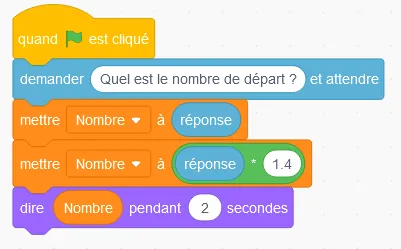


1.
Quel résultat obtient‑on lorsque l'on entre 3 comme valeur de départ ?
2.
Quel résultat obtient‑on lorsque l'on entre 23,5 comme valeur de départ ?
3.
Quel est le coefficient de proportionnalité associé à ce programme ?
4.
À quel pourcentage d'augmentation correspond ce coefficient de proportionnalité ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Exercice numérique
On considère le programme suivant :

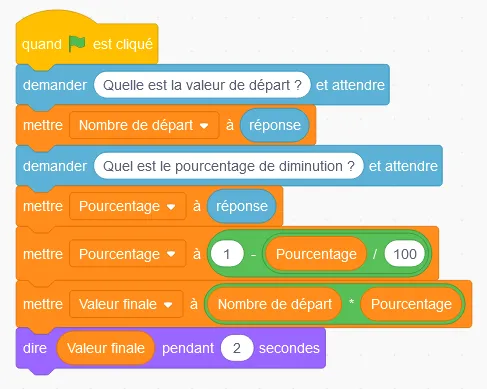
1. Quel résultat obtient‑on lorsque l'on entre 100 comme valeur de départ et 20 comme pourcentage de diminution ?
2. Quel résultat obtient‑on lorsque l'on entre 30 comme valeur de départ et 4 comme pourcentage de diminution ?
3. Quel est le coefficient de proportionnalité associé à ce programme ?


1. Quel résultat obtient‑on lorsque l'on entre 100 comme valeur de départ et 20 comme pourcentage de diminution ?
2. Quel résultat obtient‑on lorsque l'on entre 30 comme valeur de départ et 4 comme pourcentage de diminution ?
3. Quel est le coefficient de proportionnalité associé à ce programme ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

