Mathématiques Cycle 4
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Proportionnalité
Ouverturep. 123
Je découvre le chapitre
Introductionp. 124-125
J'apprends
Coursp. 126-129
Questions Flash / Je m'entraine
Exercicesp. 130-135
Problèmes résolus
Problèmesp. 136
Problèmes résolus
Problèmesp. 137
Je résous des problèmes
Exercicesp. 138-143
Exercices numériques
Exercicesp. 144
Maths autrement : Le Tour du monde en 80 jours
Travailler autrementp. 145
Je m'évalue
Exercicesp. 146
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Nos dossiers d'actualité
Dossier d'actualité
Chapitre 6
Exercices

Questions Flash - Je m'entraine

11 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions flash

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1. Il faut 6 œufs pour faire des gaufres pour 4 personnes, donc...





2. Si jʼachète 3 places de cinéma, je paie 5 €. Si jʼen achète 10, ça me coûte 15 €, donc...





3. Voici un tableau de proportionnalité. Quelle est la valeur manquante ?
    75649
    432

    4. Sur une carte à lʼéchelle \bold{1/100\:000^e}, Éric mesure la distance entre 2 villes. Il trouve 5,7 cm. La réelle distance entre ces deux villes est donc :





    5. Ce graphique représente une situation de proportionnalité.
    Graphique de la question.
    Le zoom est accessible dans la version Premium.



    6. Lʼaire de 6 carreaux est de 2 400 cm². Quelle est lʼaire de 9 carreaux ?





    7. Identifiez les grandeurs proportionnelles.





    8.  Un produit est soldé de 30 %, puis son prix est augmenté de 30 %. Son prix, par rapport au prix dʼorigine,...


    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Je m'entraine

    Reconnaitre une situation de proportionnalité
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    1
    Au supermarché.

    ✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème.

    Les carottes sont vendues à 1,80 € le kg. Les citrons sont vendus à 1 € lʼunité.

    1. Le prix des citrons est-il proportionnel à leur masse ?
     2. Peut-on dire la même chose des carottes ?
     3. À quoi le prix des citrons est-il proportionnel ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    2
    Situations de proportionnalité.

    Placeholder pour 3 tableaux.3 tableaux.
    Le zoom est accessible dans la version Premium.
    1. Quel(s) tableau(x) correspond(ent) à des situations de proportionnalité ?
    Afficher la correction
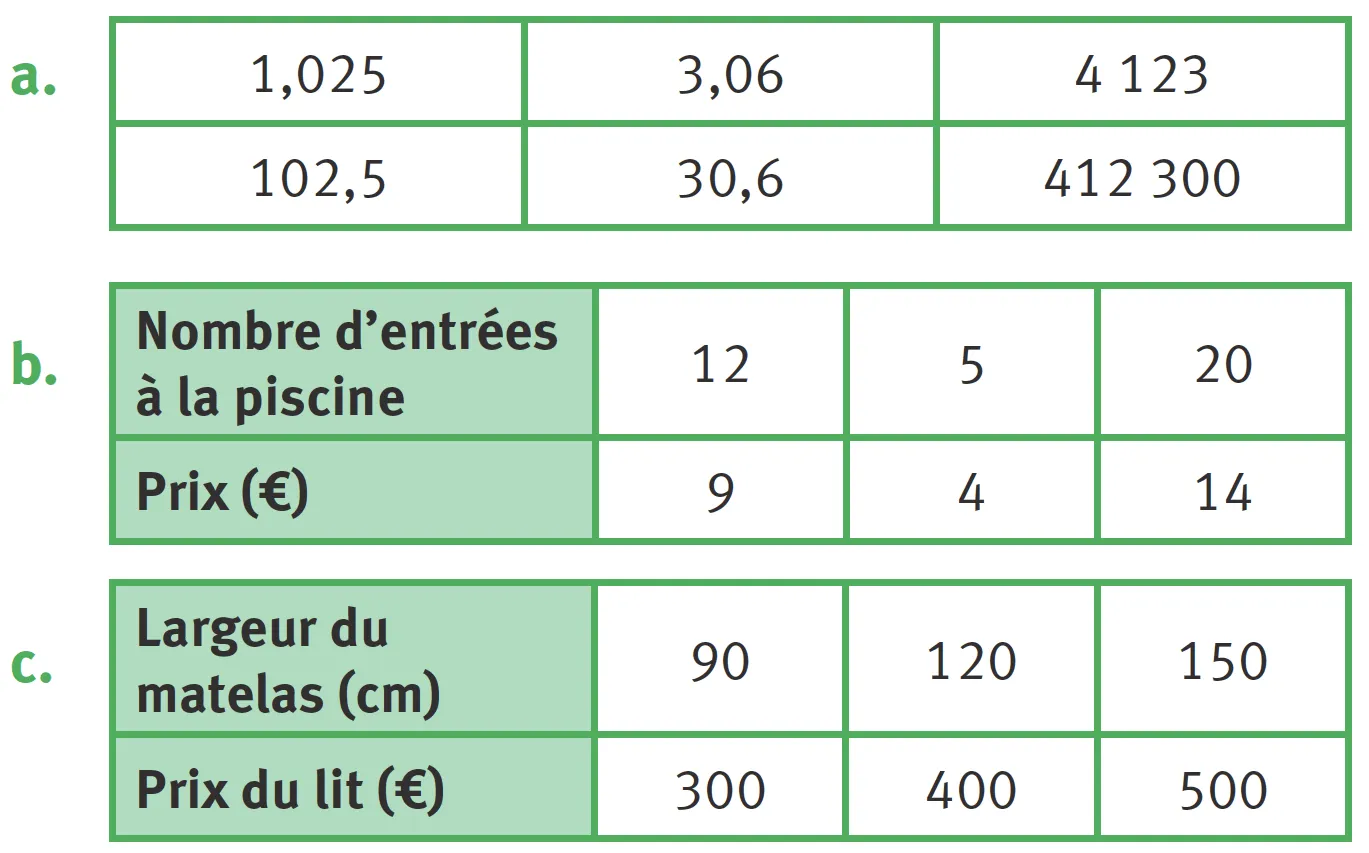
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    3
    Un enfant a normalement 28 dents.

    Quand il devient adulte, il en a 32.

    1. Le nombre de dents est-il proportionnel à lʼâge ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    5
    Pack de yaourts.

    Un pack de 6 yaourts coûte 1,50 €. Un pack de 10 yaourts de la même marque est vendu 2 €.

    1. Le prix du pack est-il proportionnel au nombre de yaourts ? Expliquez.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    4
    Situations de proportionnalité.

    ✔ Je reconnais une situation de proportionnalité.
    Placeholder pour 3 tableaux.3 tableaux.
    Le zoom est accessible dans la version Premium.
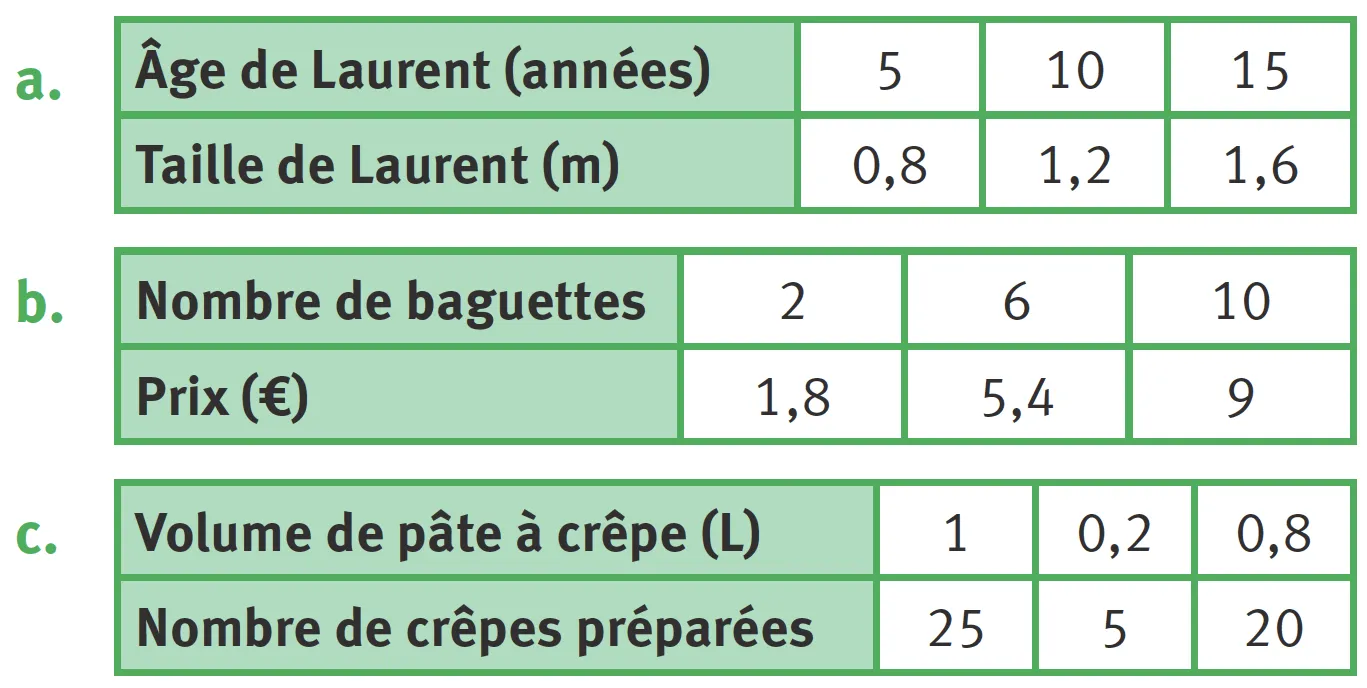    1. Parmi les situations suivantes, lesquelles sont des situations de proportionnalité ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    6
    Boites de clous.

    ✔ Je structure mon raisonnement.
    Placeholder pour Graphique lié à l'exercice 4Graphique lié à l'exercice 4
    Le zoom est accessible dans la version Premium.
    Une boite de 100 clous coûte 35 centimes. Une boite de 500 coûte 1,50 €.

    1. Le prix dʼune boite de clous est-il proportionnel au nombre de clous contenus dans la boite ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    9
    Zoé appelle Luc, qui habite en Chine.

    Après avoir saisi le numéro, elle entend : « Cet appel vous sera facturé 1,35 € puis 34 centimes par minute. »

    1. Le coût de son appel est-il proportionnel à sa durée ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    7
    Œufs à la coque.

    Pour préparer 3 œufs à la coque, il faut les plonger dans lʼeau bouillante pendant 5 minutes.

    1. Combien de temps faut-il pour préparer 4 œufs à la coque ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    8
    Dans les situations suivantes, identifiez les deux grandeurs mises en relation. Lesquelles sont des situations de proportionnalité ?

    ✔ Je sais passer du langage naturel au langage mathématique et inversement.

    1. « Christophe Lemaître court le 100 m en 10 secondes et le 400 m en 45 secondes. »
     2. « Dans 1 L de soda, il y a lʼéquivalent de 30 morceaux de sucre. »
     3. « Hier, cʼétait la fête du cinéma. Jʼai payé 5 € pour voir un premier film et, en tout, jʼai payé 8 € pour voir trois films. »
     4. « Un steak de 150 g cuit en 2 min. Il faut compter 1 min de plus si le steak pèse 100 g de plus. »
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.
    Utilisation d'un tableau de proportionnalité
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    10
    Complétez les tableaux de proportionnalité suivants.

    a.
    3 7 10 13
    		↵ x 7

    b.
    5 9 2 6
    		↵ x 0,5

    c.
    1 3,5 7 2,5
    		↵ x \frac{2}{5}

    d.
    1 2 10 6
    		6
    		↵ x 

    e.
         		5
    		20
    8
    		12 16 ↵ x 

    f.
    2 5,5 7,5
    		0,55
    		101,5 ↵ x 
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    11
    Additionnez ou soustrayez des colonnes pour compléter les tableaux de proportionnalité.

    ✔ Je combine de façon appropriée le calcul mental, posé et instrumenté.

    a.
    14 11 3 17
    18,2 14,3

    b.
    8 3 5 13
    3,2 1,2

    c.
    5 30 19 14
    		62,7 46,2

    d.
    6 7 1 13
    9 10,5

    e.
    10 6 4 16
    		57 38

    f.
    11 18 7 42
    1,65
    		1,05
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    12
    Complétez les tableaux de proportionnalité suivants.

    a.
    6 18 5
    7
    		↵

    b.
    		8 20
    1 5
    		↵

    c.
    3
    		10,5
    4 120
    		↵

    d.
    		2 200
    5
    		250 ↵
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    13
    Complétez les tableaux de proportionnalité suivants, en additionnant ou en soustrayant des colonnes.

    a.
    Nombre de gâteaux 36 132
    Nombre de paquets de gâteaux 3 11 14

    b.
    Nombre de livres rangés 117 52
    Nombre dʼétagères 9 4 5

    c.
    Volume dʼeau de mer (L) 3,8 1,1
    Masse de sel extraite (g) 96 27,5 67,5
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    14
    Complétez les tabelaux de proportionnalité suivants.

    a.
    		6
    		25
    0 2 7
    		10,5

    b.
    		18 4 5
    3 6
    		7,5

    c.
    1 2
    		8 11,5
    		14 28
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    15
    Les grandeurs suivantes sont proportionnelles.

    ✔ Je sais passer du langage naturel au langage mathématique et inversement.

    1. Une demi-baguette coûte 45 centimes. Combien coûtent 3 baguettes ?
     2. Peter court 1 km en 4 min. Quelle distance peut-il parcourir en 1 min ?
    3. 5 kg de tomates coûtent 7,20 € et 3 kg coûtent 4,32 €. Quel est le prix de 2 kg de tomates ?
     4. Il faut 3 disques durs pour stocker 690 Go de données, et 7 disques durs pour stocker 1 610 Go. Combien faut-il de disques durs pour stocker 4 600 Go de données ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    16
    Tableau de proportionnalité.

    ✔ Je combine de façon appropriée le calcul mental, posé et instrumenté.

    1. Complétez le tableau de proportionnalité suivant.

    Quantité dʼessence (L) 14 28 9 19 5
    Prix (€) 21,7
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    17
    Distance parcourue.

    Une voiture roule à une vitesse constante de 45 km/h.

    1. À lʼaide dʼun tableau de proportionnalité, déterminez la distance quʼelle parcourt en :

    10 min
    25 min
    35 min
    0,8 h
    1,5 h
    1 h 25 min
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.
    Utilisation des pourcentages
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    18
    Pourcentage.

    La classe de 3eE du collège Duruy est composée de 38 élèves, dont 16 filles.

    1. Quel est le pourcentage de filles en 3eE ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    19
    Le laiton jaune est un alliage métallique de cuivre et de zinc. Un morceau de 650 g de laiton jaune contient 403 g de cuivre.

    ✔ Je structure mon raisonnement.
    Placeholder pour Illustration de laiton jaune.Illustration de laiton jaune.
    Le zoom est accessible dans la version Premium.
    1. Quel est le pourcentage de cuivre contenu dans ce morceau de laiton jaune ?
     2. Quel est le pourcentage de zinc contenu dans ce morceau de laiton jaune ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    20
    Le maraicher.

    1. Sur les 25 kg de fraises quʼil avait récoltés Lundi, un maraicher a dû jeter 12 %. Quelle masse de fraises a-t-il jeté ?
     2. Sur les 30 kg de fraises récoltés mardi, 6 kg ont été jetés. Quel est le pourcentage de la masse des fraises qui a été jeté ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    21
    Pourcentage.

    1. Quel pourcentage du nombre de pages de ce manuel est consacré à la proportionnalité ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    22
    Parmi les 65 professeurs du collège, il y a 37 femmes.

    1. Quel est pourcentage de femmes parmi les professeurs ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    23
    Parmi les 28 élèves de la classe, un peu plus de 39 % ont 13 ans.

    1. Combien dʼélèves de la classe ont 13 ans ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    24
    Selon l'INSEE, pour le \bold4^\text{\textbf{e}} trimestre 2015, « le taux de chômage pour la France métropolitaine sʼélève à 9,9 %, soit 2,9 millions de personnes ».

    ✔ Je sais passer du langage naturel au langae mathématique et inversement.

    1. Déterminez la « quatrième proportionnelle » qui manque dans cette information et interprétez ce à quoi elle correspond.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    25
    Sophie va faire les soldes.

    Elle veut sʼacheter un pantalon rouge à 15 €. Elle a un bon de réduction de 20 %.

    1. Combien ce pantalon lui coûte-t-il ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.
    Utilisation d'échelles
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    26
    Un terrain de handball est rectangulaire. Il a les dimensions suivantes : \bold{40 \text{\textbf{~m}} \times 20 \text{\textbf{~m}}}.

    Sébastien dessine un terrain de 8 \text{~cm} \times 4 \text{~cm} sur son cahier.

    1. Quelle est lʼéchelle du dessin ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    27
    Une armoire, sur un plan dʼéchelle \bold{\dfrac{1}{15}}, a des dimensions de \bold{12 \textbf{~cm} \times 3\textbf{,}5 \textbf{~cm} \times 4 \textbf{~cm}}.

    1. Exprimez ses dimensions réelles, en m.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    28
    Sur une carte dʼéchelle \bold{\dfrac{1}{200\:000}}, la maison dʼAbdel est à 1,25 cm de son collège.

    ✔ Je structure mon raisonnement.

    1. Quelle est la distance réelle entre son collège et sa maison ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    29
    Sur une carte, on lit « 1 cm représente 10 km ».

    1. Quelle est lʼéchelle de cette carte ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    30
    La distance réelle entre les stations Vaugirard et Falguière est de 1,3 km.

    ✔ Je me repère sur une droite, dans le plan ou dans l'espace.
    Placeholder pour Graphique lié à l'exercice 12Graphique lié à l'exercice 12
    Le zoom est accessible dans la version Premium.
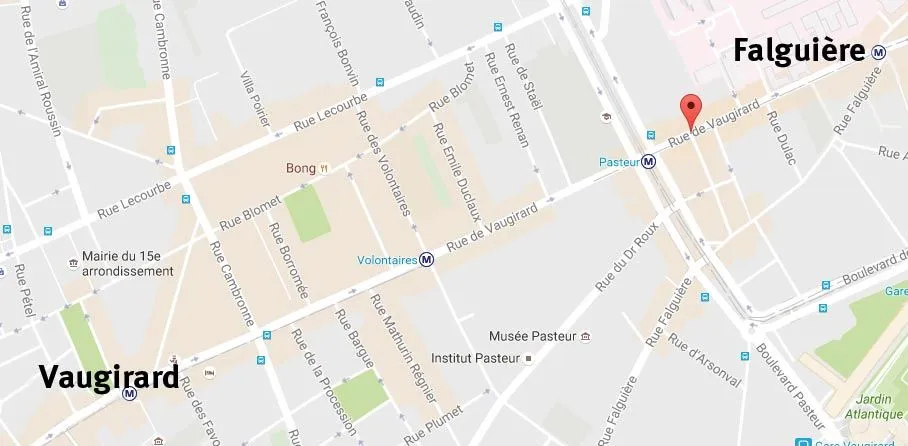    1. Déduisez-en lʼéchelle de cette carte.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    31
    Déterminez lʼéchelle de cette carte.

    ✔ J'extrais et j'exploite les informations utiles d'un document.
    Placeholder pour Graphique lié à l'exercice 13Graphique lié à l'exercice 13
    Le zoom est accessible dans la version Premium.
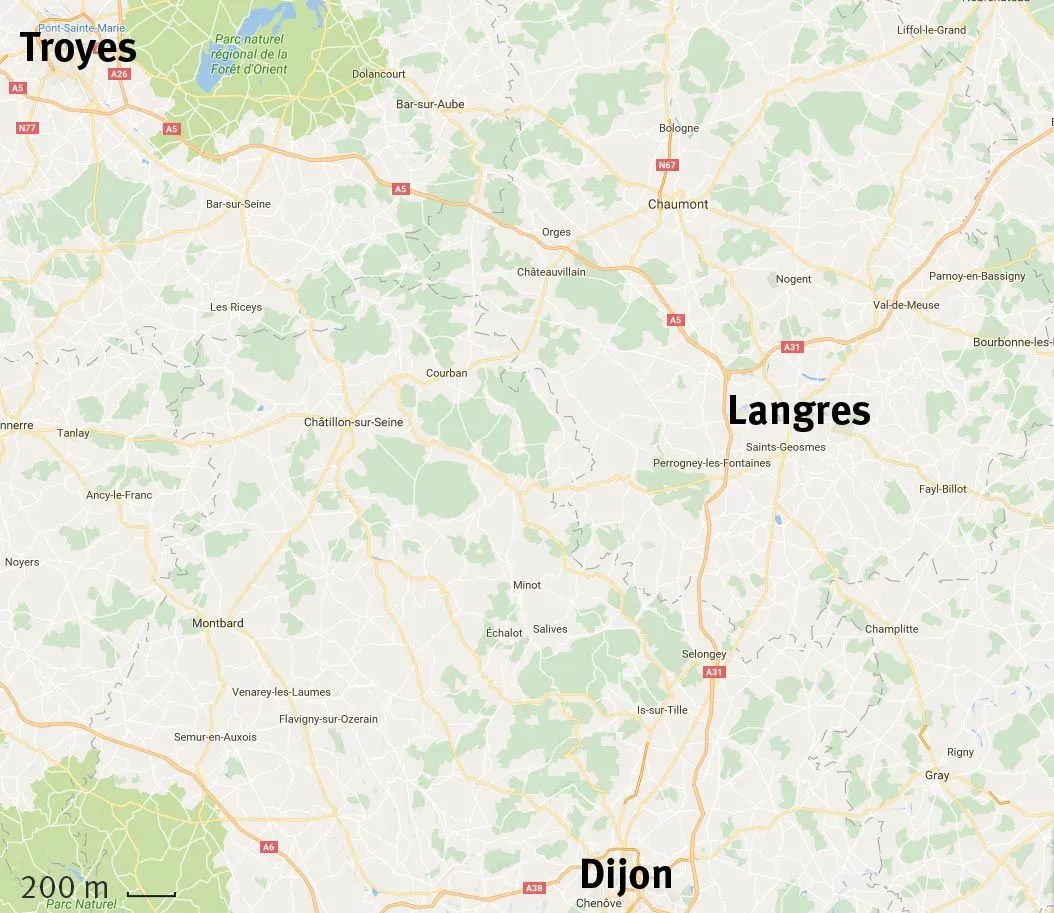    1. Déduisez-en les distances Dijon – Troyes et Dijon – Langres à vol dʼoiseau.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    32
    Un urbaniste veut représenter une rue de 3,6 km de long sur 27 m de large sur un schéma.

    1. Calculez les dimensions dʼune représentation à lʼéchelle 1/50^\text{e}.
     2. Faites de même à lʼéchelle 1/100^\text{e}.
     3. Faites de même à lʼéchelle 1/300^\text{e}.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    33
    Les grandeurs suivantes sont proportionnelles.

    Placeholder pour Tableau avec les dimensions réelles en cm: 300 / 450 / 150 / 612 / 90 et les dimensions sur le dessin en cm: 5 / 7,5 / 2,5 / 10,2 / 1,5.Tableau avec les dimensions réelles en cm: 300 / 450 / 150 / 612 / 90 et les dimensions sur le dessin en cm: 5 / 7,5 / 2,5 / 10,2 / 1,5.
    Le zoom est accessible dans la version Premium.
    1. Quel est le coefficient de proportionnalité ?
     2. Déduisez-en lʼéchelle du dessin.
    Afficher la correction
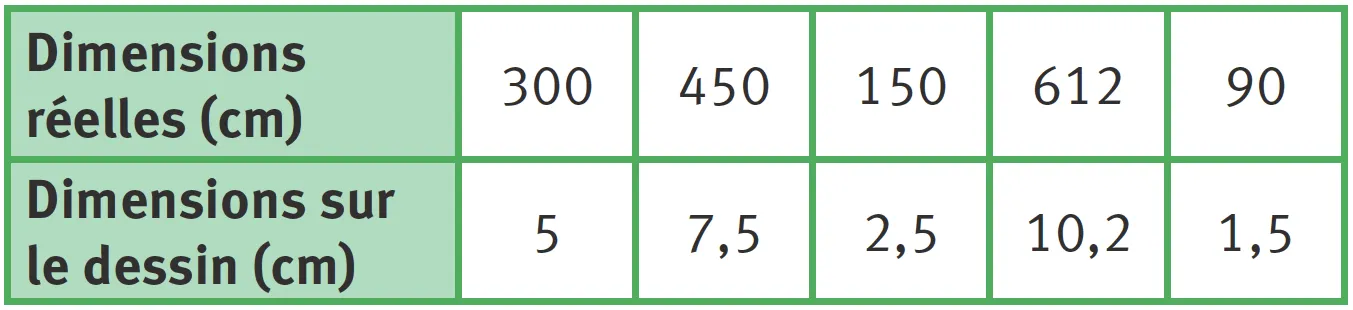
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.
    Représentation graphique d'une situation de proportionnalité
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    34
    Périmètre du carré.

    ✔ Je modélise une situation à l'aide d'une expression mathématique.

    1. Exprimez le périmètre dʼun carré en fonction de la longueur de son côté.
     2. Représentez la situation dans un repère.

    Cliquez pour accéder à une zone de dessin
    Cette fonctionnalité est accessible dans la version Premium.

    3. Sʼagit-il dʼune situation de proportionnalité ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    35
    Aire du carré.

    1. Exprimez lʼaire dʼun carré en fonction de la longueur de son côté.
     2. Représentez la situation dans un repère.

    Cliquez pour accéder à une zone de dessin
    Cette fonctionnalité est accessible dans la version Premium.

    3. Sʼagit-il dʼune situation de proportionnalité ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    36
    Quel est le prix de 13 pralinés ?

    Graphique indiquant le prix de pralinés en fonction de leur nombre.
    Le zoom est accessible dans la version Premium.
    1. Quel est le prix de 13 pralinés ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    37
    Au marché.

    1. Complétez le tableau suivant.

    Carottes (kg) 1 2 3 4
    Prix (€) 1,40

    2. Représentez la situation dans un repère orthogonal.

    Logo Geogebra

    GeoGebra

    Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail
     3. À lʼaide de la représentation graphique, donnez le prix de 2,5 kg de carottes.
     4. Quelle quantité de carottes peut-on acheter avec 5 € ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    38
    Les graphiques suivants représentent-ils des situations de proportionnalité ?

    Placeholder pour Graphiques a, b, c et d.Graphiques a, b, c et d.
    Le zoom est accessible dans la version Premium.
    a.
     b.
     c.
     d.
    Afficher la correction
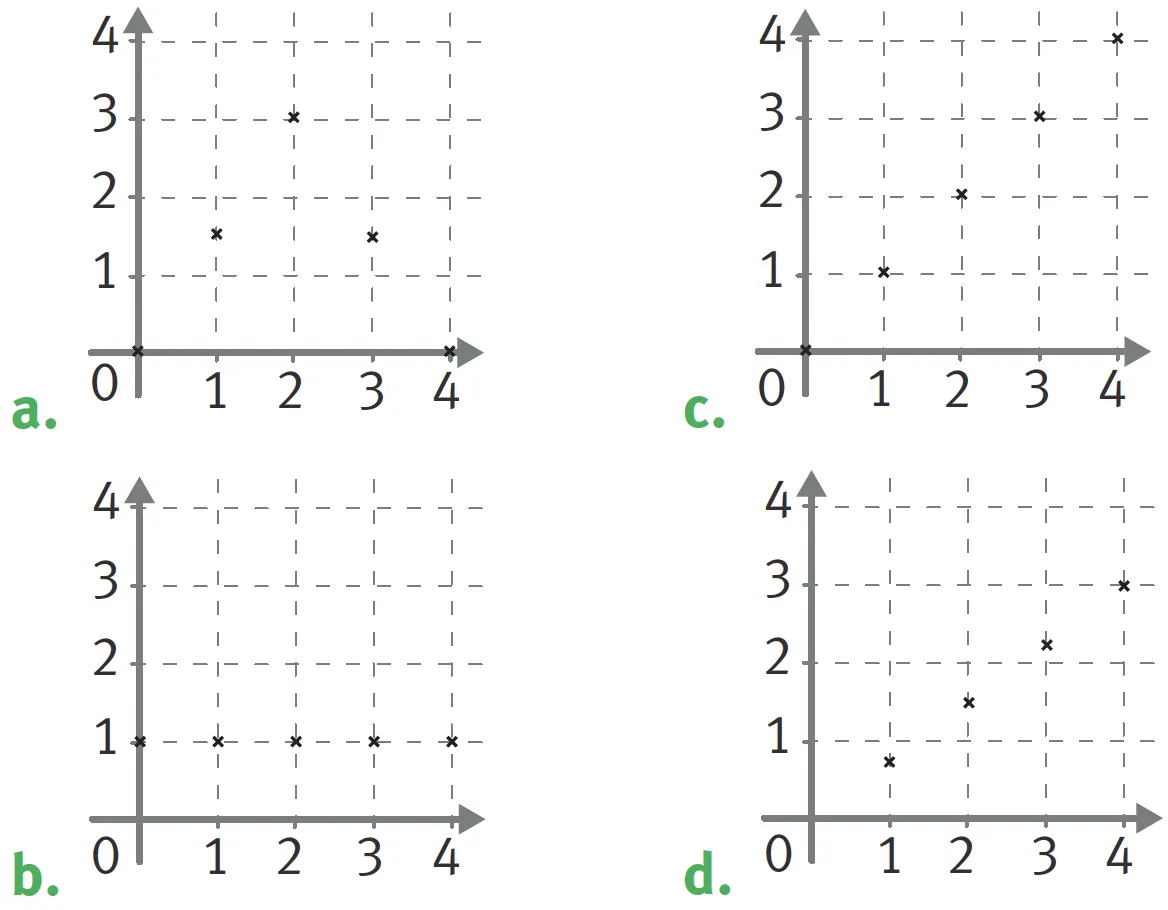
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    39
    Les graphiques suivants représentent-ils des situations de proportionnalité ?

    ✔ Je me repère sur une droite, dans le plan ou dans l'espace.

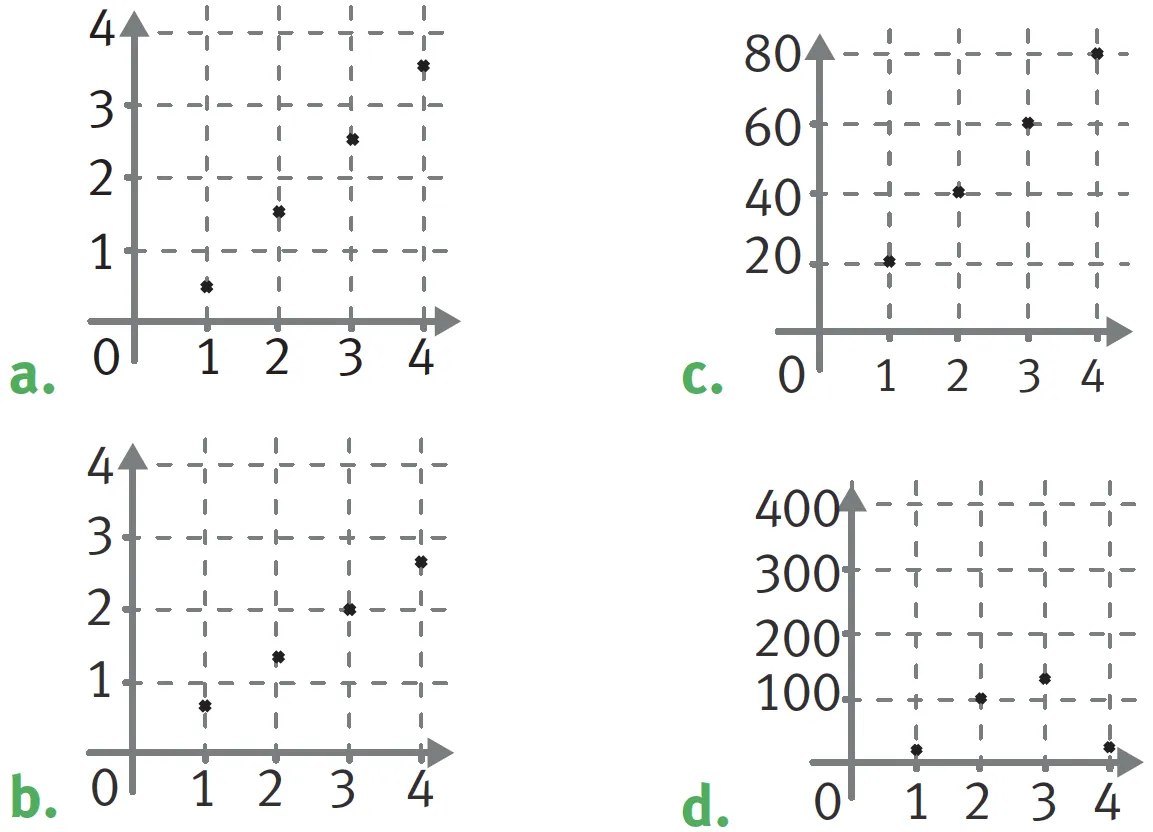    Placeholder pour Graphiques a, b, c et d.Graphiques a, b, c et d.
    Le zoom est accessible dans la version Premium.
    a.
     b.
     c.
     d.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.
    Produit en croix
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    40
    Résolvez lʼexercice sans passer par un tableau de proportionnalité.

    6 œufs coûtent 1,86 €.

    1. Quel est le prix de 10 œufs ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    41
    Résolvez lʼexercice sans passer par un tableau de proportionnalité.

    200 g de vis coûtent 1,23 €.

    1. Combien coûtent 700 g de vis ?
     2. Quelle masse de vis peut-on acheter pour 8 € ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    42
    Calculez la quatrième proportionnelle \boldsymbol{x}.

    ✔ Je combine de façon appropriée le calcul mental, posé et instrumenté.
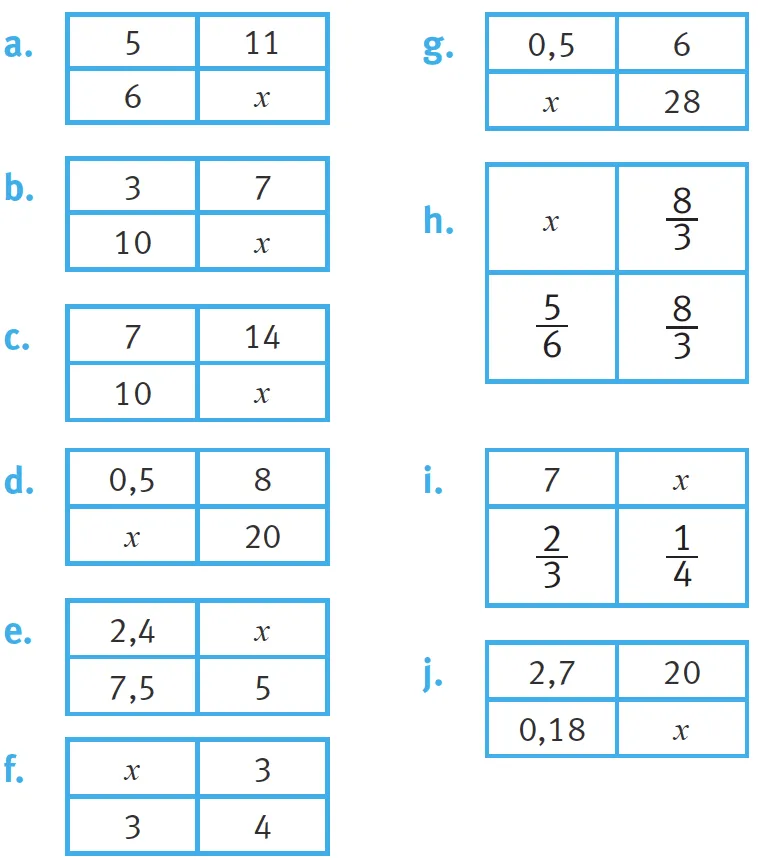
    Placeholder pour Tableaux a., b., c., d., e., f., g., h., i., j.Tableaux a., b., c., d., e., f., g., h., i., j.
    Le zoom est accessible dans la version Premium.

    a.
    b.
    c.
    d.
    e.
    f.
    g.
    h.
    i.
    j.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    43
    Calculez la quatrième proportionnelle \boldsymbol{x} lorsquʼil y a une relation de proportionnalité.

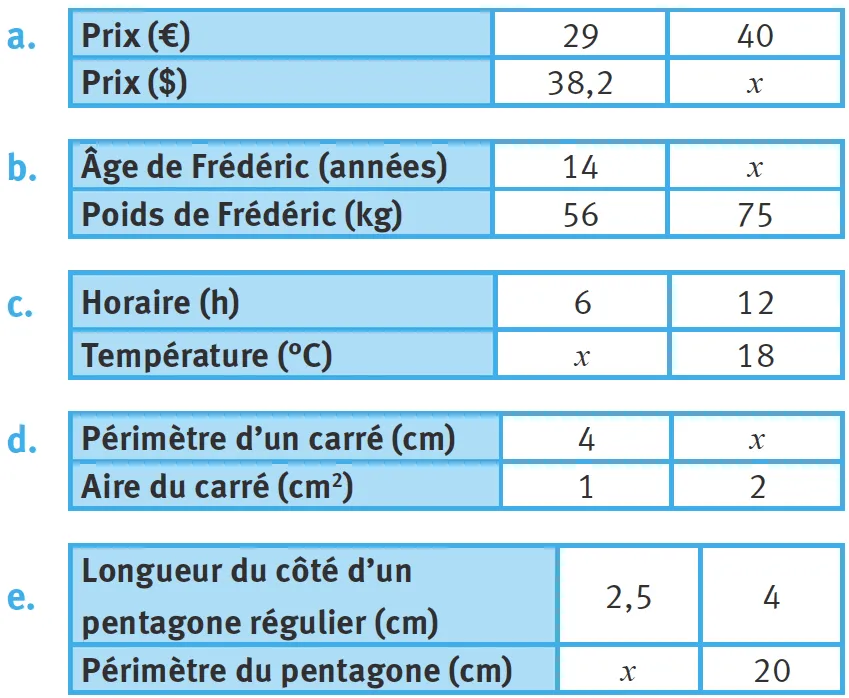
    Placeholder pour Tableaux a., b., c., d., e.Tableaux a., b., c., d., e.
    Le zoom est accessible dans la version Premium.

    a.
    b.
    c.
    d.
    e.
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Parcours de compétences

    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Énoncé

    ✔ Je reconnais une situation de proportionnalité.

    Le grand-frère de Mattéo étudie deux offres dʼemploi. Lʼentreprise A propose une rémunération proportionnelle au montant des ventes réalisées dans le mois : pour un montant de ventes de 20 000 €, son salaire serait de 1 250 €. Lʼentreprise B verserait un salaire fixe et y ajouterait un montant variable, dépendant lui aussi des ventes réalisées dans le mois.

    1. Quel serait le salaire du frère de Mattéo s‘il réalisait 17 000 € de vente dans lʼentreprise A ?
     2. Quel pourcentage du montant des ventes représente le salaire dʼun employé dans cette entreprise ?
     3. Lʼoffre dʼemploi de lʼentreprise B représente-t-elle une situation de proportionnalité ? Pourquoi ?
    Afficher la correction
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Niveau 1

    Je sais ce qu'est une situation de proportionnalité.

    Coup de pouce
    Aidez-vous de la
    partie A
     du cours p. 126.
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Niveau 2

    J'utilise les techniques de proportionnalité lorsque cela m'est explicitement demandé.

    Coup de pouce
    Dans lʼentreprise A, montant des ventes et salaire sont proportionnels.
    Construisez un tableau de proportionnalité et répondez aux questions a. et b..
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Niveau 3

    Je vérifie si une situation est de proportionnalité ou non.

    Coup de pouce
    Quelles sont les deux grandeurs analysées ?
    Expliquez dans quels cas elles sont proportionnelles.
    Ressource affichée de l'autre côté.
    Faites défiler pour voir la suite.

    Niveau 4

    J'identifie et j'exploite une situation de proportionnalité.

    Coup de pouce
    Répondez aux questions a. et b. sans passer par un tableau de proportionnalité.
    Pensez à lʼégalité des produits en croix.

    Une erreur sur la page ? Une idée à proposer ?

    Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

    Oups, une coquille

    j'ai une idée !

    Nous préparons votre pageNous vous offrons 5 essais

    Yolène
    Émilie
    Jean-Paul
    Fatima
    Sarah
    Utilisation des cookies
    Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.