Mathématiques Cycle 4
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Chapitre 12
Exercices
Questions Flash - Je m'entraine
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions flash
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Si C est le symétrique de 0 par rapport à A, alors...
a.
b.
c.
d.
2. La symétrie centrale conserve...
3. Si C est lʼimage de O par la rotation de centre A et dʼangle 82° dans le sens direct, alors...
4. La figure B est lʼimage de la figure A par la rotation de centre O dʼangle...
a.
b.
c.
d.
2. La symétrie centrale conserve...
3. Si C est lʼimage de O par la rotation de centre A et dʼangle 82° dans le sens direct, alors...
4. La figure B est lʼimage de la figure A par la rotation de centre O dʼangle...
5. Si C est lʼimage de O par la translation qui envoie A sur B, alors...
6. Si C est lʼimage de O par lʼhomothétie de centre A et de rapport 2, alors...
7. Dans quel cas la figure B est-elle lʼimage de la figure A par une homothétie ?
a.
b.
c.
d. 
6. Si C est lʼimage de O par lʼhomothétie de centre A et de rapport 2, alors...
7. Dans quel cas la figure B est-elle lʼimage de la figure A par une homothétie ?
a.
c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraine
Symétries centrales
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Symétrie.
✔ Je représente des objets et des figures géométriques
1. Reproduisez la figure suivante, puis construisez son symétrique par rapport au point O.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Symétrie.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Symétrie.
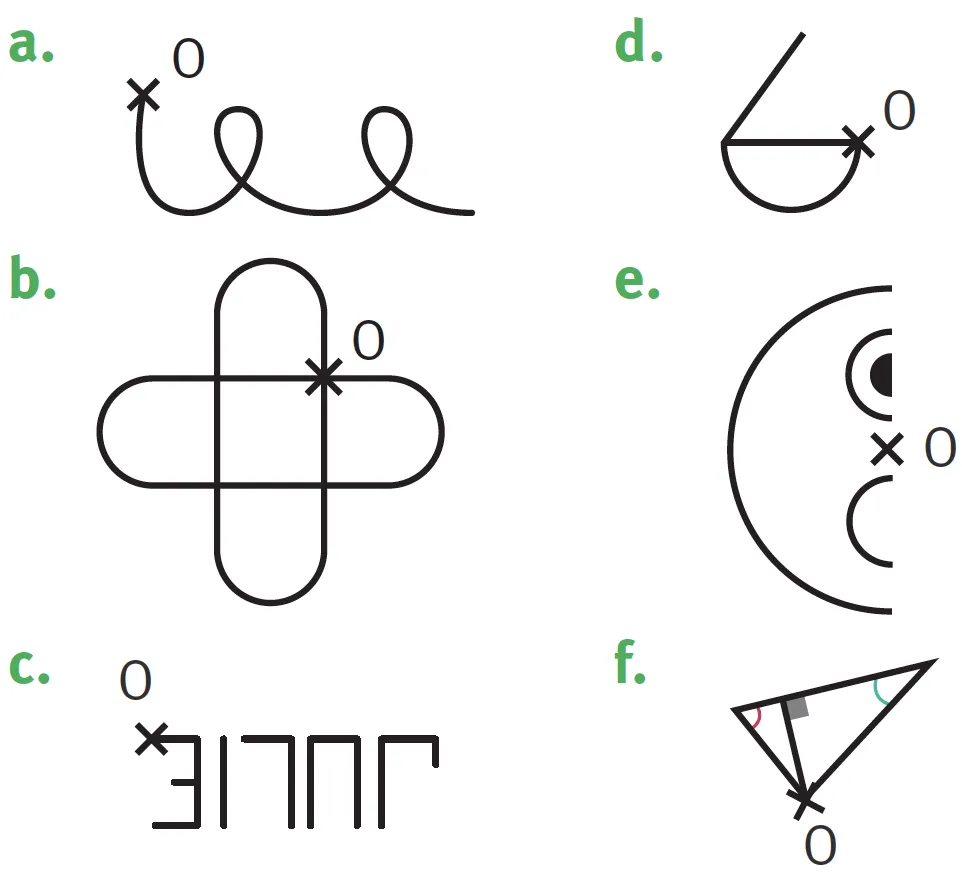
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4 Reproduisez la figure suivante.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5 Reproduisez la figure suivante.
✔ Je représente des objets et des figures géométriques
1. Construisez les points R, S et T, symétriques respectifs des points A, L et M par rapport à K. Quelle est la mesure de l'angle \widehat{\text{RST}} ?
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6 Dans la figure suivante, quatre points sont symétriques deux à deux par rapport à un point qui a été effacé.
✔ Je me repère sur une droite, dans le plan ou dans l'espace
8. Retrouvez le point qui a été effacé.
2. Quel est le point « intrus » ?
GeoGebra
2. Quel est le point « intrus » ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
7 Vrai ou faux ?
1. Choisissez la ou les bonne(s) réponse(s).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
8 Escargot
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
9 Drapeaux.
✔ Je sais passer du langage naturel au langage mathématique et inversement
1. Parmi les drapeaux suivants, quels sont ceux qui admettent des éléments de symétrie ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
10 Problème à lʼenvers.
1. Tracez un cercle C de centre O et de rayon 5 cm, placez un point A sur le cercle. Tracez un cercle C' de centre A et de même rayon que C, soit 5 cm.
2. Construisez le point F tel que C' soit le symétrique de C par rapport à F.
3. Construisez la droite d telle que C' soit le symétrique de C par rapport à d.
GeoGebra
2. Construisez le point F tel que C' soit le symétrique de C par rapport à F.
3. Construisez la droite d telle que C' soit le symétrique de C par rapport à d.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
11 Savoir refaire Le segment [CD] peut-il être le symétrique de [AB] par rapport à un point O ?
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
1. Si oui, reproduisez la figure et construisez ce point O.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
12 Tracez un cercle C de rayon 5,5 cm.
✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème
1. Placez un point A sur ce cercle.
2. Tracez le symétrique de C par rapport à A.
3. Montrez que le cercle obtenu a le même rayon que C.
GeoGebra
1. Placez un point A sur ce cercle.
2. Tracez le symétrique de C par rapport à A.
3. Montrez que le cercle obtenu a le même rayon que C.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
13 On se place dans un repère de centre O.
GeoGebra
1. Placez les points A (3 ; -2) ; B (0 ; 4) ; C (-1 ; -1) et D (2 ; 2).
2. Construisez les points E, F, G et H, symétriques respectifs de A, B, C et D par rapport à O.
3. Quelles sont les coordonnées des quatre points E, F, G et H ?
4. Que remarquez-vous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rotations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
14 Construction.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15 Rotations.
1. Montrez que lʼimage dʼun rectangle ABCD par une rotation est un rectangle A'B'C'D'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16 Rotations.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17 Savoir refaire Rotations.
✔ Je représente des objets et des figures géométriques
1. Reproduisez puis complétez le dessin afin dʼobtenir une figure et son image par la rotation de centre O, dʼangle 90° dans le sens direct.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18 Savoir refaire Symétries.
✔ Je représente des objets et des figures géométriques
1. Reproduisez cette figure.
2. Tracez son image par la symétrie d'axe (OB).
3. Tracez l'image de la figure obtenue par la rotation de centre O, d'angle 90° dans le sens indirect.
4. Tracez ensuite l'image de la figure obtenue par une symétrie centrale.
GeoGebra
2. Tracez son image par la symétrie d'axe (OB).
3. Tracez l'image de la figure obtenue par la rotation de centre O, d'angle 90° dans le sens indirect.
4. Tracez ensuite l'image de la figure obtenue par une symétrie centrale.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19 Marc décide de monter dans une grande roue. Faites un schéma de ses positions successives.
GeoGebra
1. La grande roue commence par tourner dans le sens direct de 20°.
2. Puis elle tourne dans le sens direct de 40°.
3. Elle tourne ensuite dans le sens direct de 30°.
4. Et enfin de 90° dans le sens direct.
5. À quel moment est-il le plus haut ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20 Reproduisez la figure suivante.
1. Tracez l'image ADC'D' de ABCD par la rotation de centre A, d'angle 90° dans le sens direct.
2. Tracez l'image AD'CD de ADC'D' par la rotation de centre A, d'angle 90° dans le sens direct.
3. Tracez l'image de AD'CD par la rotation de centre A, d'angle 90° dans le sens direct.
2. Tracez l'image AD'CD de ADC'D' par la rotation de centre A, d'angle 90° dans le sens direct.
3. Tracez l'image de AD'CD par la rotation de centre A, d'angle 90° dans le sens direct.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21 Reproduisez la figure suivante puis répétez sept fois la rotation de centre A, dʼangle 45° dans le sens direct.
2. Montrez que faire la rotation une huitième fois correspond à reproduire ABC.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22 Savoir refaire Rotations.
✔ Je représente des objets et des figures géométriques
1. Tracez la figure suivante et répétez trois fois la rotation dʼangle 90° dans le sens indirect.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23 Problème à lʼenvers.
1. Tracez un cercle C de rayon 2 cm, de centre O. Placez un point A sur C et tracez le cercle C' de centre A et de rayon 2 cm.
2. Construisez le point B tel que C' soit l'image par la rotation de centre B, d'angle 30° dans le sens indirect.
GeoGebra
2. Construisez le point B tel que C' soit l'image par la rotation de centre B, d'angle 30° dans le sens indirect.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Translations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24 Translations.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25 Translations.
✔ Je représente des objets et des figures géométriques
1. Reproduisez la figure puis tracez son image par la translation qui envoie A sur B.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26 Translations.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27 Savoir refaire Translations.
✔ Je représente des objets et des figures géométriques
1. Reproduisez et complétez le dessin afin dʼobtenir une figure et son image par la translation qui envoie A sur B.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28 Savoir refaire Tracez un cercle C de centre O et de rayon 2 cm.
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
1. Placez un point A sur le cercle et B l'image de O par la rotation de centre A, d'angle 45° dans le sens direct.
2. Tracez l'image de C par la translation qui envoie O vers B.
3. Montrez que le cercle obtenu a le même rayon que C.
GeoGebra
1. Placez un point A sur le cercle et B l'image de O par la rotation de centre A, d'angle 45° dans le sens direct.
2. Tracez l'image de C par la translation qui envoie O vers B.
3. Montrez que le cercle obtenu a le même rayon que C.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29 Translations.
1. Montrez que lʼimage dʼun triangle ABC rectangle en A par une translation est un triangle A'B'C' rectangle en A'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30 Translations.
1. Montrez que lʼimage dʼun triangle équilatéral ABC par une translation est un triangle équilatéral A'B'C'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31 Translations.
1. Montrez que lʼimage dʼun parallélogramme ABCD par une translation est un parallélogramme A'B'C'D'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32 Savoir refaire Translations.
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
1. Montrez que lʼimage dʼun losange ABCD par une translation est un losange A'B'C'D'.
1. Montrez que lʼimage dʼun losange ABCD par une translation est un losange A'B'C'D'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33 Translations.
1. Montrez que lʼimage dʼun rectangle ABCD par une translation est un rectangle A'B'C'D'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34 Savoir refaire Translations.
✔ Je représente des objets et des figures géométriques
1. Reproduisez la figure suivante et construisez, avec la translation qui envoie A en B, une frise composée de ce motif répété 5 fois.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Reproduisez la figure suivante.
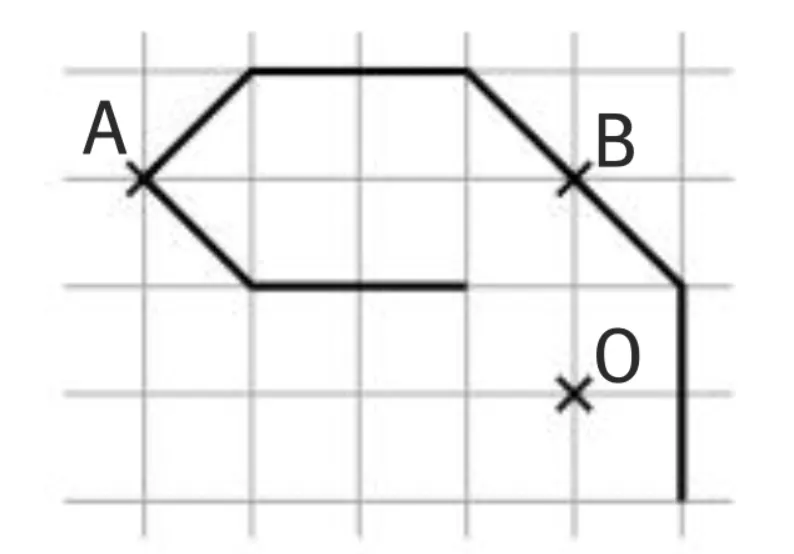
1. Tracez son symétrique par rapport au point 0 .
2. Tracez la figure F qui est l'image obtenue par la translation qui envoie A en B.
3. Tracez F^{\prime} l'image de F par cette même translation.
4. Tracez F^{\prime \prime} et F^{\prime \prime \prime} en répétant le même processus.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Homothéties
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36 Homothéties.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37 Recopiez la figure suivante et tracez son image par les homothéties suivantes.
✔ Je représente des objets et des figures géométriques
1. de centre A et de rapport 0,5.
2. de centre B et de rapport 0,5.
3. de centre C et de rapport 0,5.
2. de centre B et de rapport 0,5.
3. de centre C et de rapport 0,5.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38 Homothéties.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39 Homothéties.
GeoGebra
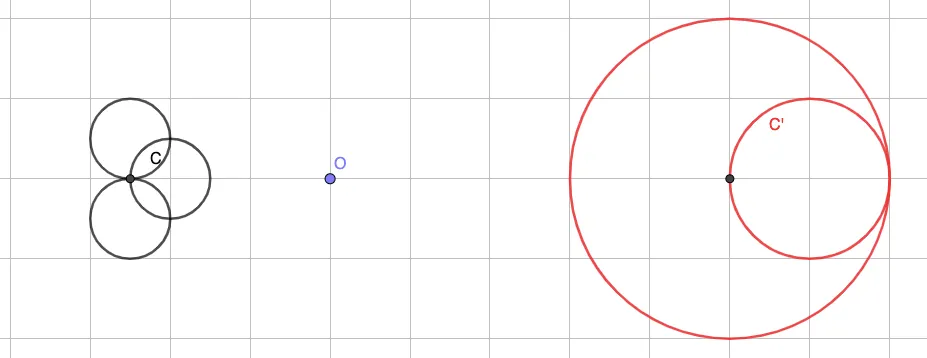
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40Homothéties.
1. Montrez que lʼimage dʼun triangle ABC équilatéral de côté x cm, par une homothétie de rapport r, est un triangle équilatéral de côté rx cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41Savoir refaire Homothéties.
✔ Je structure mon raisonnement
1. Montrez que lʼimage A'B'C'D' dʼun parallélogramme ABCD par une homothétie de centre O est un parallélogramme.
1. Montrez que lʼimage A'B'C'D' dʼun parallélogramme ABCD par une homothétie de centre O est un parallélogramme.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42 A'B'C'D' est lʼimage du parallélogramme ABCD par une homothétie de rapport r.
1. Montrez que si ABCD est un rectangle, alors A'B'C'D' est un rectangle.
2. Montrez que si ABCD est un losange, alors A'B'C'D' est un losange.
3. Montrez que si ABCD est un carré, alors A'B'C'D' est un carré.
2. Montrez que si ABCD est un losange, alors A'B'C'D' est un losange.
3. Montrez que si ABCD est un carré, alors A'B'C'D' est un carré.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43 Savoir refaire Tracez un cercle C de centre O, de rayon 1 cm.
✔ J'envisage plusieurs méthodes de résolution
Placez deux points A et B sur le cercle, puis M le symétrique de B par rapport à A. Placez enfin N l'image de B par la rotation de centre M, d'angle 130° dans le sens direct.
1. Tracez C' l'image de C par l'homothétie de centre D et de rapport 2.
2. Calculez le rayon du cercle C'.
Placez deux points A et B sur le cercle, puis M le symétrique de B par rapport à A. Placez enfin N l'image de B par la rotation de centre M, d'angle 130° dans le sens direct.
1. Tracez C' l'image de C par l'homothétie de centre D et de rapport 2.
GeoGebra
2. Calculez le rayon du cercle C'.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Parcours de compétences
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Et vous, qu'en pensez-vous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 1
Je me demande si ma réponse est cohérente.
Coup de pouce
Regardez le schéma, pensez-vous que la proposition de Yasmine soit possible ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 2
Je fais appel à la logique pour tester la cohérence de ma réponse.
Coup de pouce
Une même transformation peut-elle donner deux résultats différents ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 3
Je sais où chercher les informations qui me permettent de vérifier mon résultat.
Coup de pouce
Quelles données de l'exercice peuvent vous permettre de vous assurer du résultat ? Rappelez-vous votre cours.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Niveau 4
J'identifie les sources possibles d'incohérence.
Coup de pouce
Qu'est ce qui pousse Jasmine à penser qu'elle a trouvé l'homothétie ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
