Chapitre 12
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44Triangles et symétriques.
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
✔ Je me repère sur une droite, dans un plan ou dans l'espace
A (0 ; 0), B (2 ; 0), C (2 ; 1) et D (0 ; 1) forment un rectangle, et AB'C'D' est le symétrique de ABCD par rapport à A. E est le milieu de [B'D'] et E' le symétrique de E par rapport à A.
Vérifiez que E' est le milieu de [AC].
✔ Je me repère sur une droite, dans un plan ou dans l'espace
A (0 ; 0), B (2 ; 0), C (2 ; 1) et D (0 ; 1) forment un rectangle, et AB'C'D' est le symétrique de ABCD par rapport à A. E est le milieu de [B'D'] et E' le symétrique de E par rapport à A.
Vérifiez que E' est le milieu de [AC].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
En dessinant la figure et en traçant la position de E', il est possible de déterminer les coordonnées de E'.

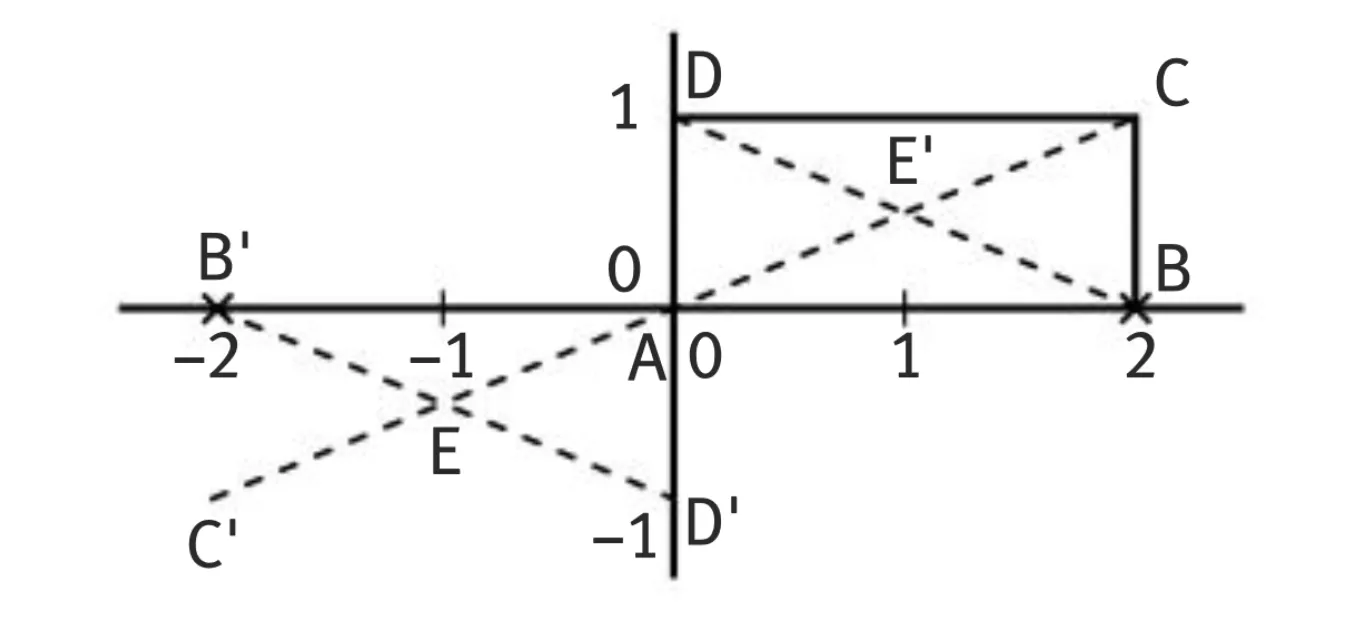
Corrigé 1


- On réalise le dessin, sur une feuille blanche ou quadrillée.
- Par symétrie (on peut aussi s'aider du quadrillage), les coordonnées des nouveaux points sont :
B' (−2 ; 0), C' (−2 ; −1) et D' (0 ; −1).
On lit que le milieu de [B'D'] est le point E (−1 ; −\dfrac{1}{2}). - Le symétrique de E est donc E' (1 ; \dfrac{1}{2}).
En le traçant, on peut vérifier, à l'aide d'une règle, que E' est bien le milieu de [AC].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Il ne faut jamais oublier que les propriétés étudiées dans d'autres classes et d'autres chapitres peuvent toujours être utilisées. Ici, les propriétés des rectangles vues en sixième peuvent être utilisées.
Corrigé 2
- B', C' et D' sont les images respectives de B, C et D par la symétrie de centre A. Donc AB'C'D' est le symétrique de ABCD par rapport à A. Or ABCD est un rectangle donc AB'C'D' est également un rectangle.
- E est le milieu de [B'D'] qui est la diagonale du rectangle AB'C'D', donc E est le milieu du rectangle AB'C'D'.
- E' est le symétrique de E par rapport à A et ABCD est également le symétrique de AB'C'D' par rapport à A. Donc E' est le milieu de ABCD.
- E' est le milieu de ABCD donc il est le milieu de ses diagonales. Donc E' est le milieu de [AC].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45Problème similaireDu rectangle au…?
1. Tracez un rectangle ABCD tel que AD = x et AB =\dfrac{x}{3}. On prendra pour x une valeur comprise entre 6 cm et 12 cm.
2. Construisez les points E, F et G, symétriques respectifs de D, A et B par rapport au point C.
3. Montrez que le quadrilatère CEFG est un rectangle de mêmes dimensions que ABCD.
4. Construisez les points H, I et J, symétriques respectifs des points C, G et F par rapport à E.
5. Montrez que le quadrilatère EHIJ est un rectangle de mêmes dimensions que CEFG.
3. Montrez que le quadrilatère CEFG est un rectangle de mêmes dimensions que ABCD.
4. Construisez les points H, I et J, symétriques respectifs des points C, G et F par rapport à E.
5. Montrez que le quadrilatère EHIJ est un rectangle de mêmes dimensions que CEFG.
6. On admet que les points A, B, J et I sont alignés. Montrez que le quadrilatère ADHI a quatre angles droits et trois côtés de même longueur.
7. Quelle est la nature de ADHI ?
7. Quelle est la nature de ADHI ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

