Nos classiques

Mathématiques Cycle 4

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Puissances
Ouverturep. 147
Je découvre le chapitre
Introductionp. 148-149
J'apprends
Coursp. 150-152
Questions Flash / Je m'entraine
Exercicesp. 153-157
Problèmes résolus
Problèmesp. 158
Problèmes résolus
Problèmesp. 159
Je résous des problèmes
Exercicesp. 160-163
Exercices numériques
Exercicesp. 164
Maths autrement : Maths et poésie
Travailler autrementp. 165
Je m'évalue
Exercicesp. 166
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Nos dossiers d'actualité
Dossier d'actualité
Chapitre 7
Exercices

Questions Flash - Je m'entraine

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions flash

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1.  Pour tous les nombres entiers n, a^{-n} est lʼopposé de a^n.





2.  La puissance (-7)^2 vaut :





3.  La puissance (-3)^{-3} vaut :








4.  C = \left(- \dfrac {1}{6} \right)^{-2}




5.  Pour calculer la puissance 10^2, il faut multiplier la base 10 avec lʼexposant 2.


6.  Soit a un entier relatif.




7.  \left(5 - \dfrac{1}{2}\right)^4 \times \left(5 - \dfrac{1}{2}\right)^{-4} = 1



8.  Si on compare les puissances 10^{100} et 100^{10}, on obtient :




9.  Quels nombres sont en écriture scientifique ?





10.  Parmi les nombres suivants, quels sont ceux qui sont plus grands que 1\:000\:000 ?





11.  Le résultat de la division \dfrac {3 \times 10^{-13}}{1\text{,}5 \times 10^{-5}} est :



Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Je m'entraine

Utilisation de puissances
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Écrivez lʼexpression sous forme de puissance.

1.  A = (-2) \times (-2) \times (-2)
 2.  B = (-4) \times (-4) \times 4 \times 4 \times 4 \times (-4)
 3.  C = (-5) \times 5 \times 5 \times 5 \times 5
 4.  D = (-2) \times 3 \times 3 \times (-2) \times 3 \times (-2) \times (-3) \times (-2)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Écrivez le produit comme une puissance dʼun nombre.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

1.  A = 3 \times 3 \times 3 \times 3 \times 3 \times 3
 2.  B = 2 \times 7 \times 2 \times 7\times 2 \times 7 \times 2 \times 7
 3.  C = (-14) \times (-14) \times (-14)
 4.  D = \pi \times \pi \times \pi \times \pi \times \pi
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Calculez les expressions suivantes.

1.  A = (-1)^1
 2.  B = (-1)^2
 3.  C = (-1)^3
 4.  D = (-1)^4
 5.  E = -1^1
 6.  F = -1^2
 7.  G = -1^3
 8.  H = -1^4
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Développez et calculez les expressions suivantes.

1.  A = 6^3
 2.  B = 4^5
 3.  C = 5^4
 4.  D = 1\:000^2
 5.  E = 10^6
 6.  F = 0\text{,}2^3
 7.  G = 1\text{,}6^2
 8.  H = 2\text{,}1^5
 9.  I = 0^{23}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Écrivez lʼexpression sous forme de puissance.

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

1.  A = 7 \times 7 \times \dfrac{1}{7} \times 7 \times 7 \times \dfrac{1}{7} \times 7
 2.  B = 9 \times 8 \times 9 \times 9 \times 9 \times 9 \times 9
 3.  C = (-6) \times (-2) \times 3 \times 6 \times 2 \times (-3)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Développez et calculez les expressions suivantes.

1.  A = (2 + 3)^5
 2.  B = (5 - 2 \times 2)^3
 3.  C = (7 - 2)^4 \times (3 + 2)^2
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

7
Développez et calculez les expressions suivantes.

1.  A = 10^{-4}
 2.  B = 6^{-2}
 3.  C = 7^{-3}
 4.  D = 8^{-1}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

8
Développez et calculez les expressions suivantes.

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

1.  A = (-5)^3
 2.  B = (-10)^7
 3.  C = (7 - 9)^5
 4.  D = (6 - 8 + 4 - 3)^{10}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

9
Développez et calculez les expressions suivantes.

1. A = 12^{-3}
 2. B = 3^{-4}
 3. C = 12^2
 4. D = 10^{-5}
 5. E = 0\text{,}01^3
 6. F = (0\text{,}2)^{-3}
 7. G = 4^3
 8. H = 5^1
 9. I = 3^4
 10.  J = 1^{13}
 11.  K = 0^{25}
 12.  L = 11^3
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

10
Calculez les expressions suivantes.

1.  A = \dfrac{6^3}{10}
 2.  B = (1 - 0\text{,}7)^3
 3.  C = 2 - 0\text{,}7^3
 4.  D = 20\text{,}4 + (-2)^4
 5.  E = (8 + 2)^4
 6.  F = \left(\dfrac{6}{10}\right)^3
 7.  G = 150 + (8 + 2)^4
 8.  H = 150 + 8 + 2^4
 9.  I = 150 - (-8 - 2)^4
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

11
11 : Calculez de tête.

✔ Je combine de façon appropriée le calcul mental, posé et instrumenté

1.  A = 2^3
 2.  B = (-2)^4
 3.  C = 2^{-3}
 4.  D = 4^2
 5.  E = (-4)^2
 6.  F = 2^4
 7.  G = \left(\dfrac{1}{2}\right)^3
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

12
Déterminez le signe des nombres suivants.

1.  A = -1\text{,}3^5
 2.  B = \left(-\dfrac{2}{3}\right)^9
 3.  C = - (-5)^4
 4.  D = \dfrac{(-2)^9}{(-3)^9}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

13
Déterminez le signe des expressions suivantes.

Soit a un nombre positif différent de zéro et n un entier.

a. a^2 ;
b. -a^2 ;
c. (-a)^2 ;
d. a^3 ;
e. -a^3 ;
f. (-a)^3 ;
g. a^n ;
h. -a^n ;
i. (-a)^n
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

14
Réduisez les expressions suivantes.

1.  5^{42} \times 5^{54} ; 5^{220} \times 5^{-75} ; 5^{25} \times 5^{45} \times 5^{20}
 2.  \dfrac{5^{326}}{5^{63}} ; \dfrac{5^{-25}}{5^{55}} ; \dfrac{5^{143}}{5^{-66}} ; \dfrac{5^{-44}}{5^{107}}
 3.  (5^{42})^{10} ; (5^{24})^{-4} ; (5^{-9})^{-6} ; ((5^{-9})^4)^2
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

15
Recopiez en les complétant les expressions suivantes.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

5 ... \times 5^3 = ... ^{16} = 25^87^6 \times 7^4 = 49 ...4 ... \times 8^3 = 2 ...2 ... \times 9^3 = 18^3

5 
 \times 5^3 =
^{16} = 25^8
7^6 \times 7^4 = 49

4
\times 8^3 = 2

2
\times 9^3 = 18^3

Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

16
Les nombres suivants sont-ils plus grands que 1 ?

1.  2^2 ; \left(\dfrac{1}{2}\right)^2 ; 4^{-4} ; (-2)^4
 2.  \left(\dfrac{1}{2}\right)^{-2} ; -\dfrac{1}{2^{-2}} ; \dfrac{1^{-2}}{2} ; \left(\dfrac{1}{4}\right)^{-4}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

17
Vrai ou faux ? Corrigez si nécessaire.

✔ Je sais passer du langage naturel au language mathématique et inversement

1.  9^{-1} est l'inverse de 9.
 2.  2^{-1} est l'opposé de 2.
3.  1 est l'inverse de 1^{-1}.
 4.  -1^4 est l'opposé de -1.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

18
Ces égalités sont-elles vraies ?

1.  6^3 = 3^3 \times 2^3



2.  8^4 = 2 \times 4^4



3.  9^5 = 4^5 + 5^5



4.  10^8 = ((3 + 7)^2)^4

Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

19
Ces égalités sont-elles vraies ?

1.  (6^5)^2 = (3^5)^2 \times 4^5



2.  60^9 = 2^{18} \times 15^9



3.  (18 + 4)^5 \times 3^9 = 3^{17} + 4^5 \times 3^9 + 2^5 \times 3^5


Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Calculs avec les puissances
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

20
Calculez les expressions suivantes.

1.  A = 2^3 \times 2^1
 2.  B = 100^2 \times 100^2
 3.  C = 10^5 \times 10^3
 4.  D = 6^{-3} \times 6^5
 5.  E = 10^{-1} \times 10^{-2}
 6.  F = 5^2 \times 2^5
 7.  G = 3^2 \times 3^{-2}
 8.  H = 2^{-3} \times 2^{-3}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

21
Simplifiez puis calculez.

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

1.  A = \dfrac{10^8}{10^{12}}
 2.  B = \dfrac{10^3}{10^{-4}}
 3.  C = \dfrac{2^{-3}}{2^{-5}}
 4.  D = \dfrac{10^{-13}}{10^2}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

22
Calculez les expressions suivantes.

1.  A = 10 - (5^2)^2
 2.  B = ((10 - 5)^2)^2
 3.  C = (10^3)^5 - (10^5)^3
 4.  D = (10^4)^2 - (10^2)^3
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

23
Calculez en faisant attention aux priorités de calcul.

1.  A = (5 + 3)^4
 2.  B = 5^4 + 3^4
 3.  C = \dfrac{(5 +3)^4}{(5^4 + 3^4)}
 4.  D = \dfrac{5^4}{3^4} + \dfrac{3^4}{5^4}
 5.  E = 5 \times 3^4
 6.  F = 5^4 \times 3^4
 7.  G = (5 \times 3)^4
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

24
Simplifiez si possible en une puissance de 10.

1.  A = 10^3 \times 10^5
 2.  B = (10^6)^4
 3.  C = 6 \times 10^3 + 3 \times 10^2 + 1 \times 10^1
 4.  D = \dfrac{10^{-3}}{10^4}
 5.  E = \dfrac{(10^3)^4}{10^{-5}}
 6.  F = \dfrac{3 \times 10^{-14} \times 10^{-3}}{(10^6)^2}
 7.  G = \dfrac{4 \times 10^2 \times 10}{(10^{-3})^2}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

25
Calculez de tête.

✔ Je combine de façon appropriée le calcul mental, posé et instrumenté

1.  A = 3^4 + 7^4
 2.  B = (3 +7)^4
 3.  C = 2^6 \times 5^6
 4.  D = (2 \times 5)^6
 5.  E = 10^3 - 8^3
 6.  F = (10 - 8)^3
 7.  G = 8^3 \div 4^3
 8.  H = (8\div 4)^3
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

26
Calculez de tête.

1.  A = -3 \times 2^{-2}
 2.  B = (-5)^3
 3.  C = 3 \times (-2)^4
 4.  D = (-5 \times 4)^{-2}
 5.  E = -3^2 \times (-5)^2
 6.  F = (-2)^2 \times (-3)^2
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

27
Calculez les expressions suivantes.

✔ J'exprime mes résultats dans les unit"s et écritures les plus adaptées

1.  A =\dfrac{(5+3)^4}{4^4}
 2.  B = \dfrac{(6 + 10)^{10}}{2^{10}}
 3.  C = \dfrac{(99 - 19)^{10}}{(36 + 4)^{10}}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

28
Calculez les expressions suivantes.

1.  A = \dfrac{(54 + 46)^7}{(65 - 15)^8}
 2.  B = \dfrac{5^{10} + 5^{12}}{5^4}
 3.  C = \dfrac{60^{10}}{2^{21} \times 3^{11}}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

29
Calculez lʼexpression suivante.

1.  \dfrac{12^9 \times 3^{19}}{(2^5 \times 3^4)^3} \div 9^9
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

30
Exprimez sous la forme a \times b^n.

1.  A = 2^4 \times 3^5 + 6^4 \times 3
 2.  B = 7^3 \times 2^6 + 14^3 \times 7
3.  C = 3^7 \times 2^{15} - 12^8
 4.  D = \dfrac{(5 - 8)^9 \times 2^{10} \times 5^{14}}{30^{10}}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Lʼécriture scientifique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

31
Écrivez sous la forme de puissances de 10.

1.  A = 0\text{,}001
 2.  B = 1\:000\:000\:000
 3.  C = 0\text{,}00\:000\:001
 4.  D = 1
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

32
Ces nombres sont-ils en écriture scientifique ?

1.  A = 2\text{,}261^{34}



2.  B = 17\text{,}5 \times 10^9



3.  C = 8\text{,}93251 \times 100^{-7}



4.  D = 9\text{,}8 \times 100^{11}



5.  E = 1\text{,}118 \times 10^{10}



6.  F = 3\text{,}654 \times 5^{12}



7.  G = 78 \times (5 \times 2)^3


Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

33
Donnez lʼécriture scientifique des nombres suivants.

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

1.  A = 437\:850\:000\:000
 2.  B = 0\text{,}00000416
 3.  C = 1\:593\text{,}28
 4.  D = 0\text{,}00000000181
 5.  E = 17\text{,}4 \times 10^9
 6.  F = 9\text{,}8 \times 100^{11}
 7.  G = 56\text{,}753219
 8.  H = 0\text{,}67842 \times 10^6
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

34
Les calculs ci-contre sont-ils corrects ?

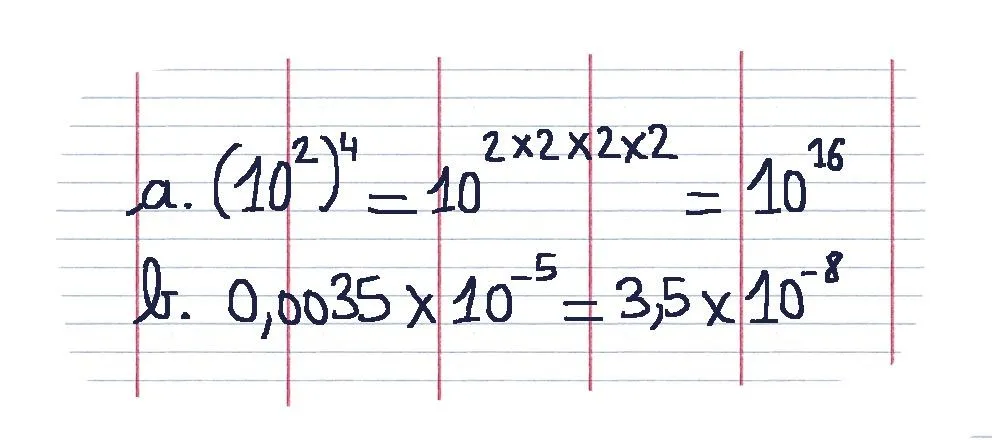
Placeholder pour Photographie de calculs mathématiques manuscrits : puissance de 10 et notation scientifique.Photographie de calculs mathématiques manuscrits : puissance de 10 et notation scientifique.
Corrigez dans le cas contraire.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

35
Donnez lʼécriture scientifique des nombres suivants.

1.  A = 87\:000\:000
 2.  B = 0\text{,}00045
 3.  C = 291 \times 10^{-7}
 4.  D = 0\text{,}052 \times 10^5
 5.  E = 89\:789 \times 10^9
 6.  F = 3\:000\:006 \times 10^{-6}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

36
Puissance de 10.

Complétez à lʼaide dʼune puissance de 10.

234\text{,}43 \times
= 0\text{,}0023443
0\text{,}3 \times
  = 3\:000
0\text{,}0072 \times
 = 7\text{,}2
0\text{,}0000875 \times
 = 8\text{,}75
5\text{,}63 \times
 = 563\:000
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

37
Les nombres suivants sont-ils exprimés en notation scientifique ?

✔ J'exerce mon esprit critique pour vérifier la cohérence des résultats

1.  A = \dfrac{6}{7} \times 10^{-10}



2.  B = -10\text{,}01 \times 10^8



3.  C = -9\text{,}38 \times 10^{12}



4.  D = 4\text{,}97677 \times 10^{-4}



5.  E = -0\text{,}81 \times 10^2



6.  F = 4\:763 \times 10^{-3}



7.  G = 2\text{,}004 \times 10^{28}



8.  H = -1\text{,}08 \times 10^{-42}



9.  I = 0\text{,}004 \times 10^3


Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

38
Donnez lʼécriture scientifique des nombres suivants.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

1.  A = 3\:627\text{,}1
 2.  B = 0\text{,}0356
 3.  C = -198 \times 10^{-4}
 4.  D = -2\:636 \times 10^4
 5.  E = \dfrac{8}{5}
 6.  F = 10\text{,}89 \times 10^{-27}
 7.  G = -34\:567\:890 \times 10^2
 8.  H = 0\text{,}12 \times 10^4
 9.  I = \sqrt{144} \times 10^{-28}
 10.  J = -\dfrac{4}{5} \times 10^{18}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

39
Donnez lʼécriture scientifique des nombres suivants.

1.  A = 5\:900\:000
 2.  B = 0\text{,}000000008
 3.  C = 30\:200\:000
 4.  D = 0\text{,}00001002
 5.  E = 350 \times 10^6
 6.  F = 0\text{,}00053 \times 10^{-5}
 7.  G = 4\:100 \times 10^{12}
 8.  H = 0\text{,}011500 \times 10^{23}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

40
Donnez lʼécriture scientifique des nombres suivants.

1.  A = 20^7 \times 5^7
 2.  B = 200^3 \times 0\text{,}00052^2
 3.  C = 5 \times 10^3 \times (2 \times 10^{-2})^3
 4.  D = 5^{-1} \times 10^3
 5.  E = \dfrac{28 \times 10^4}{0\text{,}4 \times 10^7}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

41
Classez les nombres suivants dans lʼordre croissant.

 \text{\textless}
\lt
\text{\textless}
\text{\textless}
\text{\textless}
\text{\textless}
\text{\textless}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

42
Savoir refaire
Donnez lʼécriture scientifique de cette expression.

✔ Je décompose un problème en sous-problème pour le simplifier et le résoudre

\dfrac{(5 \times 10^6 \times 7 \times 10^{-8})^3 \times 64 \times 10^3}{25 \times 10^5 \times 8 \times 10^{-9} \times 7 \times 10^4}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

44
Écriture scientifique.

✔ J'exerce mon esprit critique pour vérifier la cohérence des résultats

1. Complétez pour que les valeurs soient écrites en écriture scientifique.

  • La diagonale dʼun ordinateur mesure 3\text{,}378 \times
    mm.
  • Paris est à 3\text{,}94 \times
     cm de Lyon.
  • Un terrain de foot fait 1\text{,}2 \times
    km de long.
  • Une fourmi mesure 2\text{,}5 \times
     m.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

43
Savoir refaire
Calculez et exprimez le résultat sous la forme la plus simple possible.

✔ J'utilise l'écriture d'un nombre la plus appropriée pour calculer

Pour les résultats décimaux, donnez lʼécriture scientifique.

1.  A = 0\text{,}534 + 322 \times 10^{-3}
 2.  B = 5 \times 10^{-4} + 3 \times 10^{-3} + 4 \times 10^{-2}
 3.  C = 0\text{,}425 + 7 \times 10^{-4} + 23 \times 10^{-2}
 4.  D = 5^{-2} \times 10^{-4}
 5.  E = \dfrac{3 \times 10^{15} - 24 \times 10^{14}}{3 \times 2 \times 10^{-20}}
 6.  F = \dfrac{22 \times 10^{-10} \times 27 \times 10^{-6}}{32 \times 10^{-15}}
 7.  G = \dfrac{5^3 \times 3^8 \times 5^2}{125 \times 5^2 \times 81 \times 7^0}
 8.  H = (2 \times 100)^3 \times (5 \times 10^{-5})^2
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
Savoir refaire
Donnez lʼécriture scientifique des nombres suivants.

✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

1.  200^3 \times 0\text{,}0005^2
 2.  16^3 \times 8^6
 3.  3^{-6} \times 81^2
4.  36^3 \times 3^{-12} \times 2^{-12}
 5.  4\:000 \times 0\text{,}000005
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Parcours de compétences

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

✔ Je combine de façon appropriée le calcul mental, posé et instrumenté.

Mattéo met Yasmine au défi de calculer le produit de 16 000 000 par 390 625 sans calculatrice. Il lui donne un indice : 390\:625 = 25^4. Yasmine réfléchit à haute voix : « 16 vaut 24 donc 16 000 000 sʼécrit comme 2^4 multiplié par une puissance de 10. Avec ça et ton indice, pas besoin de calculatrice pour trouver la réponse ! »

Relevez à votre tour le défi de Mattéo.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 1

Je connais les différents outils de calcul à ma disposition.

Coup de pouce
Quelles touches de la calculatrice vous permettent de calculer un carré ? Une puissance ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 2

Je calcule en utilisant la méthode qui m'est indiquée.

Coup de pouce
À lʼaide de la calculatrice, vérifiez lʼindice de Mattéo. Puis, par écrit, retrouvez la puissance de 10 qui, multipliée à 24, donne 16 000 000.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 3

Je choisis une méthode de calcul et je l'applique dans la question.

Coup de pouce
Avec lʼaide de Mattéo et le raisonnement de Yasmine, avez-vous besoin de la calculatrice ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Niveau 4

Je combine les différentes méthodes à ma disposition pour calculer plus efficacement.

Coup de pouce
Pour aller plus vite, pensez aux propriétés de calcul des puissances.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.