Maths autrement : Méthodes de cryptage

Jules César (100 av. J.-C. - 44 av. J.-C.) a laissé son nom à un type de codage : le chiffrement de César. En effet, lors de certaines correspondances qu’il voulait tenir secrètes, César remplaçait chaque lettre par la lettre de l’alphabet située trois rangs plus loin.

Jules César

Envie d’en savoir plus ? Découvrez d’autres moyens de codage avec :

• des disque de codage avec le chiffre de César ;
• et la machine Enigma.

Exercice 1 : Étape 1 : Chiffre de César : principe

Voici une roue pour coder et décoder. Par exemple, A (sur le petit disque) devient H (sur le grand disque) donc le chiffre de César (le décalage) est 7.

1

Codez le mot « OUI » avec un décalage de 10.

2

Décodez ce message, sachant que le décalage est de 21 : « GRKG PGIZG KYZ ».

Exercice 2 : Étape 2 : Chiffre de César : décodage

Pour décrypter le mot : « WLSJNUAY », nous allons tester tous les décalages possibles en utilisant le tableur. Entrez le texte crypté sur la première ligne et les décalages à tester dans la première colonne avec, une colonne sur deux, la proposition du texte de départ.Nous allons utiliser différentes fonctions du tableur : CODE() permet de transformer une lettre en nombre. Par exemple : CODE(“A”) = 65. MOD( ; ) renvoie le reste dʼune division euclidienne : MOD(30;26) = 4. CAR() est lʼinverse de la fonction CODE(). Par exemple : CAR(70) = F.

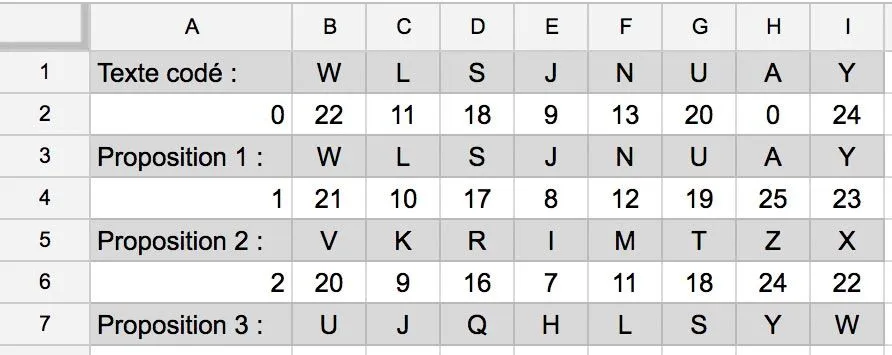
1

Expliquez à quoi correspond la formule =MOD(CODE(B1)-$A2-65;26) entrée en B2.

2

Quelle formule faut-il écrire en B3 pour obtenir la lettre de lʼalphabet dont le rang est la valeur en B2 ? (On considère que le rang de A est 0.)

Exercice 3 : Étape 3 : Le cryptage affine

On choisit une fonction affine. Chaque lettre est remplacée par son rang dans lʼalphabet, en partant de zéro : A est codé par 0, B est codé par 1, etc. On calcule lʼimage de ces nombres par la fonction affine. On détermine le reste dans la division euclidienne de ces images par 26. On décode chaque nombre par la lettre de lʼalphabet correspondante : 0 devient A, 1 devient B, etc.

1

En utilisant la fonction $f : x \mapsto 11 x + 2$, cryptez le mot « AFFINE ».

2

Voici un message codé par fonction affine à coeffficients entiers : « SNMS RSKE RDLD HDMS RHKX RVPR KER ». Sachant que A est codé F et K est codé J, retrouvez le message.