Chapitre 1
J'apprends
Arithmétique
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ADivision euclidienne et critères de divisibilité
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Rappel sur la division euclidienne
Rappel
Effectuer la division euclidienne d'un dividende par un diviseur, c'est trouver deux nombres appelés quotient et reste tels que :
- Le dividende, le diviseur, le quotient et le reste sont des entiers ;
- Dividende = diviseur × quotient + reste ;
- Le reste est plus petit que le diviseur.

Exercices n° p. 19
J'applique
Consigne : Quels sont le quotient et le reste de la division de 247 par 22 ?
Correction :
Le quotient est 11, le reste 5, et on peut écrire :
247 = 22 \times 11 + 5.

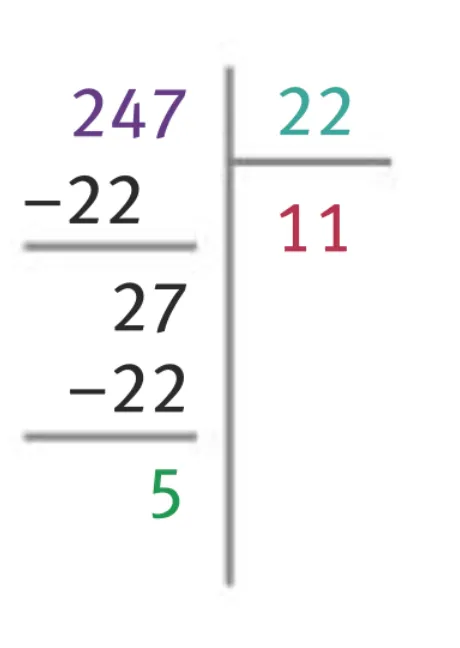
Attention
Dans toute division, le diviseur n'est jamais égal à 0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Divisibilité dʼun nombre
Définitions
Si le reste de la division euclidienne de \color{#6e2d88}a par \color{#3ab4e0}b est nul alors on dit que :
- \color{#3ab4e0}b est un diviseur de \color{#6e2d88}a ;
- \color{#6e2d88}a est un multiple de \color{#3ab4e0}b.
Exercices n° p. 19-20
Exemple :
- 2 est un diviseur de 10 car 2 \times 5 = 10.
- 3 et 4 sont des diviseurs de 156 car 3 \times 4 \times 13 = 156.
J'applique
Consigne :5 est-il un diviseur de 30 ?
Correction :
5 \times 6 = 30, donc 5 est un diviseur de 30.
Remarques :
- Si a est multiple de b, et b diviseur de a, alors le reste de la division euclidienne de a par b est nul.
- Tout entier naturel admet au moins le nombre 1 et lui-même comme diviseurs.
Rappel
- Tout nombre est divisible par 2 si son dernier chiffre est 0, 2, 4, 6 ou 8.
- Tout nombre est divisible par 3 si la somme de ses chiffres est divisible par 3.
- Tout nombre est divisible par 4 si ses deux derniers chiffres forment un nombre multiple de 4.
- Tout nombre est divisible par 5 si son dernier chiffre est 0 ou 5.
- Tout nombre est divisible par 9 si la somme de ses chiffres est un multiple de 9.
- Tout nombre est divisible par 10 sʼil se termine par 0.
Exercices n° p. 19-20
J'applique
Consigne :
Trouvez quatre diviseurs de 150.
Correction :
- 150 est un nombre entier, il est donc divisible par 1.
- 150 a comme chiffre des unités 0, il est donc divisible par 2.
- La somme des chiffres composant 150 est égale à 1 + 5 = 6, qui est un multiple de 3, il est donc divisible par 3.
- 150 a comme chiffre des unités 0, il est donc divisible par 5.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3 Je perfectionneNombres premiers
Définition
Un entier positif est un nombre premier sʼil possède exactement deux diviseurs distincts : 1 et lui-même.
Exercices n° p. 20
- 1 a un unique diviseur, lui-même. Ce nʼest donc pas un nombre premier.
- 0 a une infinité de diviseurs. Ce nʼest donc pas un nombre premier.
- 2 est le seul nombre premier pair. Tous les autres nombres pairs ont au moins trois diviseurs : 1, 2 et eux-mêmes.
J'applique
Consigne :
4 est-il un nombre premier ?
Correction :
4 a trois diviseurs : 1, 2 et 4. Il nʼest donc pas premier.
4 est-il un nombre premier ?
Correction :
4 a trois diviseurs : 1, 2 et 4. Il nʼest donc pas premier.
Consigne :
Quels sont les dix premiers nombres premiers ?
Correction :
2 ; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 ; 23 ; 29.
Quels sont les dix premiers nombres premiers ?
Correction :
2 ; 3 ; 5 ; 7 ; 11 ; 13 ; 17 ; 19 ; 23 ; 29.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BPriorités de calcul
Je découvre
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1 Calcul sans parenthèses
Propriété
Dans une expression numérique sans parenthèses, on effectue
- Dʼabord les multiplications et les divisions, de gauche à droite ;
- Puis les additions et les soustractions, également de gauche à droite.
Exercices n° p. 20-21
J'applique
Consigne :
Calculez \text{A} = 20 - 2 \times 3 + 12 \div 6.
Correction :
- La multiplication et la division sont prioritaires : on effectue les calculs de gauche à droite.
\text{A} = 20 - 2 \times 3 + 12 \div 6
\text{A} = 20 - 6 + 12 \div 6
Donc \text{A} = 20 - 6 + 2. - Il ne reste alors que des additions et des soustractions, quʼon effectue de gauche à droite.
\text{A} = 20 - 6 + 2
\text{A} = 14 + 2
Donc \text{A} = 16.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2 Calcul avec parenthèses
Propriété
- Dans une expression numérique qui contient des parenthèses, on effectue :
- En priorité les calculs entre les parenthèses ;
- Puis on procède comme pour une expression numérique sans parenthèses.
- Quand il y a des parenthèses imbriquées, on effectue dʼabord les calculs entre les parenthèses les plus intérieures.
Exercices n° p. 21-23
J'applique
Consigne : Calculez \text{C} = (3 \times (7 - 3)) + 1.
Correction :
- Les calculs entre les parenthèses sont prioritaires : on effectue dʼabord ceux entre les parenthèses les plus intérieures.
\text{C} = (3 \times (7 - 3)) + 1 - On effectue les calculs entre les parenthèses extérieures.
\text{C} = (3 \times 4) + 1
\text{C} = 12 + 1
Donc \text{C} = 13.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
