Chapitre 17
Exercices
Je résous des problèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25Triangle ABC.
Le triangle ABC est rectangle en A, BC = 6,8 cm et AC = 6 cm.
 On place deux points I et J respectivement sur les segments [BC] et [AC].
On place deux points I et J respectivement sur les segments [BC] et [AC].
1. Les droites (AB) et (IJ) sont-elles parallèles ?

1. Les droites (AB) et (IJ) sont-elles parallèles ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26Savoir refaireRegardez dans le miroir.

1. Quelle est la hauteur de l'arbre ?
Coup de pouce
Quand une image se
répercute sur un miroir, elle a le même
angle d'entrée que de sortie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27Tour Eiffel.

Madame Cheez souhaite prendre une photo originale de la tour Eiffel. Elle souhaite en fait que sa main semble toucher le sommet de la tour sur la photo. Sa main est à 1,5 m du sol alors que la tour Eiffel mesure 324 m de haut pour 124,9 m de large. Pour cela, son mari doit se placer à 2 m d'elle pour prendre la photo en se positionnant au ras du sol.
1. Déterminez, en justifiant et en détaillant les calculs, la distance au sol séparant la main de Madame Cheez et la tour Eiffel.
1. Déterminez, en justifiant et en détaillant les calculs, la distance au sol séparant la main de Madame Cheez et la tour Eiffel.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Savoir refaireUne bouteille de parfum.

Un parfumeur conçoit un nouveau flacon pour sa marque. Celui-ci a la forme de la pyramide SABC à base triangulaire de hauteur [AS].
On sait que :
1. Calculez le volume de la pyramide SABC (arrondi au cm^{3} près).
2. Pour fabriquer son bouchon SS'MN, les concepteurs ont coupé cette pyramide par un plan P parallèle à sa base et passant par le point S' tel que SS' = 6 cm.
a. Quelle est la nature de la section plane S'MN obtenue ?
b. Calculez la longueur S'N.
3. Calculez le volume maximal de parfum en cm^{3} que peut contenir ce flacon en le remplissant jusquʼà la base du bouchon.
On sait que :
- ABC est un triangle rectangle et isocèle en A ;
- AB = 7,5 cm et AS = 15 cm.
1. Calculez le volume de la pyramide SABC (arrondi au cm^{3} près).
a. Quelle est la nature de la section plane S'MN obtenue ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29Programme de construction.

1. Construisez un triangle ABC quelconque et les points (D, E, F, G, H, I, J) comme suit.
- Sur [AB], placez un point D.
- Le point E apartenant à [BC] tel que (DE) // (AC).
- Le point F appartenant à [AC] tel que (EF) // (AB).
- Le point G appartenant à [AB] tel que (FG) // (BC).
- Le point H appartenant à [BC] tel que (GH) // (AC).
- Le point I appartenant à [AC] tel que (HI) // (AB).
- Le point J appartenant à [AB] tel que (IJ) // (BC).
2. Quelle conjecture semble-t-il raisonnable de faire sur D et J ?
3. Calculez AJ à lʼaide de AB, de AC et de AI.
4. Calculez AJ à lʼaide de AB, AC et de CI.
5. Calculez AJ à lʼaide de AC, de CB et de CH.
6. Déduisez-en que \dfrac{\text{AJ}}{\text{BH}}=\dfrac{\text{AB}}{\text{CB}}.
7. Grâce à la réponse précédente, quelle conjecture peut-on faire entre les longueurs AJ, DB, AI et CI ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30Savoir refaireQui a raison ?

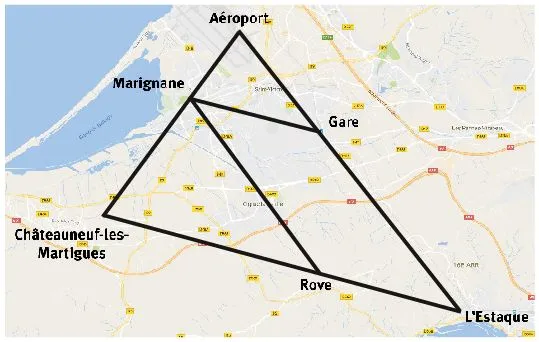
Agnès et Patrick habitent à Châteauneuf-les-Martigues (noté par le point C). Patrick prétend que la distance à vol dʼoiseau entre Châteauneuf et lʼaéroport (A) est plus grande que celle entre Châteauneuf et Rove (R). Agnès nʼest pas dʼaccord.
Données :
1. Calculez CM.
2. Calculez CR.
3. Concluez.
Données :
- (MG) // (CE) et (MR) // (AE) ;
- AM = 3 km ; MG = 4,8 km ; CE = 13 km ; AE = 12,2 km et MR = 8 km.
1. Calculez CM.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31Parallélogramme et théorème de Thalès.
ABCD est un parallélogramme.
AB = 6 cm, AD = 4,5 cm et DB = 7,5 cm.
Le point E de [DB] est tel que EB = 3,5 cm. Les droites (EC) et (AB) se coupent en F, les droites (EC) et (AD) en G.
AB = 6 cm, AD = 4,5 cm et DB = 7,5 cm.
Le point E de [DB] est tel que EB = 3,5 cm. Les droites (EC) et (AB) se coupent en F, les droites (EC) et (AD) en G.
1. Construisez la figure en grandeur réelle.
2. Quelle est la nature du triangle BAD ?
3. Qu'en déduisez-vous pour ABCD ? Pour le triangle FAG ? Pour le triangle BFC ?
4. Calculez FB puis FC, FA, GA et GF. En déduire GC.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32 Vers le Brevet (Amérique du Nord, 2015).
Pour filmer les étapes d'une course cycliste, les réalisateurs de télévision utilisent des caméras installées sur deux motos et d'autres dans deux hélicoptères. Un avion relais, plus haut dans le ciel, recueille les images et joue le rôle d'une antenne relai. On considère que les deux hélicoptères se situent à la même altitude et que le peloton des coureurs roule sur une route horizontale. Le schéma illustre cette situation.


L'avion relais (point A), le premier hélicoptère (point L) et la première moto (point N) sont alignés.De la même manière, l'avion relais (point A), le deuxième hélicoptère (point H) et la deuxième moto (point M) sont également alignés.
On sait que AM = AN = 1 km ; HL = 270 m et AH = AL = 720 m.
1. Relevez la phrase de l'énoncé qui permet d'affirmer que les droites (LH) et (MN) sont parallèles.
2. Calculez la distance MN entre les deux motos.
On sait que AM = AN = 1 km ; HL = 270 m et AH = AL = 720 m.
1. Relevez la phrase de l'énoncé qui permet d'affirmer que les droites (LH) et (MN) sont parallèles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33Thalès, parallèles et triangle isocèle.
ABC est un triangle isocèle en A et A' le pied de la hauteur issue de A. P est un point de [AA'] distinct de A et de A'. La parallèle à (AB) passant par P coupe [BC] en M. La parallèle à (AC) passant par P coupe [BC] en N.
1. Tracez la figure.
2. Montrez que A' est le milieu de [MN].
1. Tracez la figure.
2. Montrez que A' est le milieu de [MN].
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34Vers le Brevet (Métropole, 2015).

Le triangle JAB est rectangle en A.
1. Calculez la longueur JB.
2. Montrez que la longueur AC est égale à 5,4 m.
3. Calculez l'aire du triangle JCB.
- Les droites (MU) et (AB) sont parallèles.
- Les points A, M et J sont alignés.
- Les points C, U et J sont alignés.
- Les points A, C et B sont alignés.
- AB = 7,5 m ; MU = 3 m ; JM = 10 m ; AJ = 18 m.
1. Calculez la longueur JB.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35Raphaël et Tarek rénovent un vieux grenier.
Ils veulent savoir si deux poutres superposées notées [DE] et [BC] sont bien parallèles entre elles et par rapport au sol. Mais aucun des deux n'a pensé à amener de niveau. Heureusement, à deux, ils ont de bons souvenirs de leur programme de mathématiques de 3e. Ils réalisent le schéma de la situation.

- La toiture est un triangle AFG isocèle en A. [AH] est la hauteur issue de A relative à [FG].
- A, B, D, F et A, C, E, G sont alignés dans cet ordre.
- B est le milieu de [AD].
- Les droites (AH), (CD) et (BE) se coupent toutes trois en I.

1. Pour chacune de leurs affirmations, dites s'ils
ont raison ou tort.
a. « On peut représenter notre problème comme une configuration de Thalès ; il y en a même quatre sur la figure », s'écrie Tarek après avoir dessiné la figure précédente. Tarek a-t-il raison ?
b. « Il nous faut d'abord savoir si (BC), (DE) et (FG) sont parallèles, et il n'y a que trois configurations potentielles », corrige Raphaël. A-t-il raison ?
c. « Certes, mais il nous suffit de deux égalités de rapports pour savoir si les poutres [BC], [DE] et le sol [FG] sont parallèles entre eux », réplique Tarek. Est-ce vrai ?
d. « Par exemple, si \dfrac{\text{BC}}{\text{DE}} = \dfrac{\text{CI}}{\text{ID}}, on aura déjà montré que [BC] et [DE] sont parallèles », propose Raphaël. Raphaël a-t-il raison ?
e. « Non, il faut vérifier si \dfrac{\text{BI}}{\text{IE}}=\dfrac{\text{CI}}{\text{ID}} ou encore si \dfrac{\text{AB}}{\text{AD}}=\dfrac{\text{AC}}{\text{AE}} pour prouver que [BC] et [DE] sont parallèles », rectifie Tarek. Qu'en pensez-vous ?
a. « On peut représenter notre problème comme une configuration de Thalès ; il y en a même quatre sur la figure », s'écrie Tarek après avoir dessiné la figure précédente. Tarek a-t-il raison ?
2. On donne AF = AG = 10 cm, AD = 6 cm et EG = 4 cm. Qu'en déduisez-vous pour [DE] et [FG] ? Qu'en déduisez-vous pour le triangle ADE ?
3. Dans le triangle ADE, quelle est la nature de la droite (AI) ? La droite (EI) ? Montrez que (DI) est la médiane de ADE relative à [AE]. Que pouvez- vous en déduire pour le point C ?
4. Concluez quant au problème posé par Tarek et Raphaël.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36Royaume-Uni.
Le drapeau du Royaume-Uni est surnommé « Union Jack ». Il rassemble les drapeaux de l'Angleterre, du Pays de Galles, de l'Écosse et de l'Irlande du Nord.
On le représente sous la forme d'un rectangle ABCD, de ses diagonales [AC] et [BD], et des médiatrices [EF] et [GH] de sa longueur et sa largeur.

On le représente sous la forme d'un rectangle ABCD, de ses diagonales [AC] et [BD], et des médiatrices [EF] et [GH] de sa longueur et sa largeur.

1. Faites un schéma de l'Union Jack. Combien de configurations de Thalès sont représentées sur ce drapeau ?
2. On pose x la largeur du drapeau. Sa longueur vaut le double de sa largeur. Exprimez la longueur du drapeau en fonction de x. Quelle est la longueur d'une diagonale ? Calculez ces trois mesures pour x = 1 cm, x = 2 cm et x = 4 cm.
3. Tracez ce rectangle dans le cas où x = 4 cm. On note I l'intersection des diagonales et on place le point J sur [AC] tel que AJ = 2 cm. Tracez la parallèle à (BD) passant par J. Elle coupe (AB) en K, (AD) en L et (CD) en M.
4. Calculez IJ. Déduisez-en MD, JL, JK, AK et AL en précisant à chaque fois la configuration de Thalès retenue. Calculez ID. Déduisez-en JM.
5. Déterminez la nature du quadrilatère KMDB.
4. Calculez IJ. Déduisez-en MD, JL, JK, AK et AL en précisant à chaque fois la configuration de Thalès retenue. Calculez ID. Déduisez-en JM.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
37Vers le Brevet (Polynésie française, 2009).
Dans un verre à pied ayant la forme d'un cône de révolution dans sa partie supérieure, on verse du sirop de menthe jusqu'à la hauteur IR, puis de l'eau jusqu'à la hauteur IF.
Les points I, R et F sont alignés ainsi que les points I, S et G. On donne RS = 3 cm, FG = 7,5 cm et IF = 8 cm.

Les points I, R et F sont alignés ainsi que les points I, S et G. On donne RS = 3 cm, FG = 7,5 cm et IF = 8 cm.

1. Pour démontrer que les droites (RS) et (FG) sont parallèles, quelle propriété faut-il utiliser?
2. Calculez IR.
3. Quelles sont les proportions de sirop de menthe et d'eau dans le verre ? Quelle quantité de sirop faut-il pour faire 15 litres de boisson ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
38Calculez h.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
39Hypothèse.
(GF) et (CD) sont parallèles, de même que (FE) et (BC).
 1. Que pouvez-vous dire des rapports \dfrac{\text{AG}}{\text{AD}} , \dfrac{\text{AF}}{\text{AC}} , \dfrac{\text{AE}}{\text{AB}} ?
2. Écrivez les égalités de Thalès pour les triangles DBA et GEA.
3. Que pouvez-vous dire de (BD) et (EG) ?
1. Que pouvez-vous dire des rapports \dfrac{\text{AG}}{\text{AD}} , \dfrac{\text{AF}}{\text{AC}} , \dfrac{\text{AE}}{\text{AB}} ?
2. Écrivez les égalités de Thalès pour les triangles DBA et GEA.
3. Que pouvez-vous dire de (BD) et (EG) ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
40Vers le Brevet (Pondichéry, 2013).
SABCD est une réduction de la pyramide du Louvre. Cʼest une pyramide régulière qui a pour base le carré ABCD. Son volume est égal à 108 cm^{ 3} et sa hauteur [SH] mesure 9 cm.




1. Vérifiez que l'aire de ABCD est bien 36 cm^{2}. Déduisez la mesure de AB. Donnez une valeur approchée du périmètre du triangle ABC.
2. SMNOP est une réduction de la pyramide SABCD. On obtient alors la pyramide SMNOP telle que l'aire du carré MNOP soit égale à 4 cm^{2}.
a. Calculez le volume de la pyramide SMNOP.
b. Élise pense que pour obtenir le périmètre du triangle MNO, il suffit de diviser le périmètre du triangle ABC par 3. Êtes-vous d'accord avec elle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
41Section dʼune pyramide.
La pyramide EABCD a une base carrée telle que AB = 6 cm et EA = 8 cm. On pose I appartenant à [EA] tel que EI = 3 cm. On coupe cette pyramide par un plan parallèle à sa base passant par I.
1. Quelle est la nature de la section ?
1. Quelle est la nature de la section ?
2. Quel est le coefficient de réduction ?
3. Quelle est l'aire de la section ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
42Savoir refaireTriangle CAM.
CAM est un triangle tel que AC = 4,5 cm, AM = 6 cm et CM = 7,5 cm.
1. Tracez le triangle CAM.
2. Quelle est la nature de CAM ?
3. On place le point B quelconque sur (CM) tel que B n'appartient pas au triangle CAM. Tracez la perpendiculaire à (AC) passant par B. Elle coupe [AC] en N.
1. Tracez le triangle CAM.
2. Quelle est la nature de CAM ?
4. Démontrez que (AM) et (BN) sont parallèles.
5. Calculez BN et CN dans le cas où BC = 8 cm.
6. Même question si BC = 10 cm.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
43Vers le Brevet (Nouvelle-Calédonie, 2013).
En se retournant lors d'une marche arrière, le conducteur d'une voiture voit le sol à 6 m derrière sa voiture. Sur le schéma, la zone grisée correspond à ce que le conducteur ne voit pas lorsqu'il regarde en arrière.
Données : (AE) // (BD) ; AE = 1,50 m ; BD = 1,10 m ; EC = 6 m.

Données : (AE) // (BD) ; AE = 1,50 m ; BD = 1,10 m ; EC = 6 m.

1. Calculez DC.
2. Déduisez-en que ED = 1,60 m.
3. Une fillette mesure 1,10 m. Elle passe à 1,40 m derrière la camionnette. Le conducteur peut-il la voir ? Expliquez.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
44Vers le Brevet (Métropole, 2013).
Dans les marais salants, le sel récolté est stocké sur une surface plane. On admet qu'un tas de sel a toujours la forme d'un cône de révolution.
Pascal souhaite déterminer la hauteur d'un cône de sel de diamètre 5 m. Il possède un bâton de longueur 1 m. Il effectue des mesures et réalise les deux schémas suivants.


Pascal souhaite déterminer la hauteur d'un cône de sel de diamètre 5 m. Il possède un bâton de longueur 1 m. Il effectue des mesures et réalise les deux schémas suivants.


1. a. Démontrez que la hauteur de ce cône de sel est égale à 2,50 m.
b. Déterminez le volume en \text{m}^{3} de sel contenu dans ce cône. Arrondissez le résultat au \text{m}^{3} près.
2. Le sel est ensuite stocké dans un entrepôt sous la forme de cônes de volume 1 000\text{~m}^{3}. Par mesure de sécurité, la hauteur d'un tel cône de sel ne doit pas dépasser 6 m. Quel rayon faut-il prévoir au minimum pour la base ? Arrondissez le résultat au dm près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45Droites parallèles et perpendiculaires ?
Sur la figure :
- les points K, A, F, C sont alignés ;
- les points G, A, E, B sont alignés ;
- (EF) et (BC) sont parallèles ;
- AB = 5 et AC = 6,5 ;
- AE = 3 et EF = 4,8 ;
- AK = 2,6 et AG = 2.

1. Démontrez que BC = 8.
2. Tracez en vraie grandeur la figure complète en prenant comme unité le centimètre.
3. Les droites (KG) et (BC) sont-elles parallèles ? Justifiez.
4. Les droites (AC) et (AB) sont-elles perpendiculaires ? Justifiez.
3. Les droites (KG) et (BC) sont-elles parallèles ? Justifiez.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46Vers le Brevet (Polynésie française, 2010).
Thalès de Millet (624 av. J.-C. - 547 av. J.-C.) se rendit célèbre en donnant la hauteur de la plus grande pyramide d'Égypte. KEOP est un carré de centre H et de côté 230 m. [SH] est la hauteur de cette pyramide. I est le milieu de [OE].


1. Calculez HI.
2. On se place à l'extérieur de la pyramide et on plante verticalement un bâton de 2 m représenté par le segment [AB] de façon à ce que A, I et H soient alignés. On place le point M, tel que les points M, B, S et M, A, H soient alignés. On sait que MA = 2,4 m et MH = 165 m. Calculez SH.
3. Calculez le volume de cette pyramide. Arrondissez le résultat au \text{~m}^{3}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47Boite de chocolats.
Une boite de chocolats a la forme dʼune pyramide tronquée.
 Le rectangle ABCD de centre H et le rectangle A'B'C'D' de centre H' sont dans des plans parallèles.
Le rectangle ABCD de centre H et le rectangle A'B'C'D' de centre H' sont dans des plans parallèles.
On donne : AB = 6 cm ; BC = 18 cm ; HH' = 8 cm ; SH = 24 cm.

On donne : AB = 6 cm ; BC = 18 cm ; HH' = 8 cm ; SH = 24 cm.
1. Calculez le volume V_1 de la pyramide SABCD de hauteur SH.
2. Quel est le coefficient k de la réduction qui permet de passer de la pyramide SABCD à la pyramide SA'B'C'D' de hauteur SH' ?
3. Déduisez en le volume V_2 de la pyramide SA'B'C'D' puis le volume V_3 de la boite de chocolats.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exercice numérique
Le père de Julien vient d'acheter une nouvelle voiture. Le concessionnaire lui a offert une miniature de cette voiture à l'échelle 1/24.
1. Sachant que la longueur de la voiture est de 4,470 m, déterminer la longueur de la miniature.
2. Sachant que l'aire du pare‑brise est de 1,96 dm², déterminer l'aire du pare‑brise miniature.
3. Sachant que le volume du coffre est de 500 dm3, déterminer le volume du coffre miniature.
1. Sachant que la longueur de la voiture est de 4,470 m, déterminer la longueur de la miniature.
2. Sachant que l'aire du pare‑brise est de 1,96 dm², déterminer l'aire du pare‑brise miniature.
3. Sachant que le volume du coffre est de 500 dm3, déterminer le volume du coffre miniature.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Exercice numérique
On réalise une maquette à l'échelle 1/150.
1. Quelle est la longueur réelle d'un élément mesurant 10 cm ?
2. Quelle est l'aire réelle d'un élément de 3 cm2 ?
1. Quelle est la longueur réelle d'un élément mesurant 10 cm ?
2. Quelle est l'aire réelle d'un élément de 3 cm2 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tâche complexeJeu de billes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Mathieu veut créer un jeu de billes formé de bâtons de bois et de deux fois deux barres de métal.Lʼobjectif est que la bille parte du point A et arrive seule au point B.
1. À quelle vitesse la bille arrivera-t-elle au point B ?
1. À quelle vitesse la bille arrivera-t-elle au point B ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1Vitesse de la bille.
Dans ce jeu, quand la bille descend, sa vitesse augmente de 2 cm/s à chaque cm parcouru. Quand elle monte, sa vitesse diminue de 3 cm/s par cm parcouru. Elle part sans aucune vitesse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Le jeu.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


