Chapitre 17
Problèmes résolus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23Cratère de volcan.
✔ Je choisis un cadre adapté (numérique, algébrique ou géométrique) pour traiter un problème
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème
✔ Je fais appel à mes connaissances pour comprendre et résoudre un problème

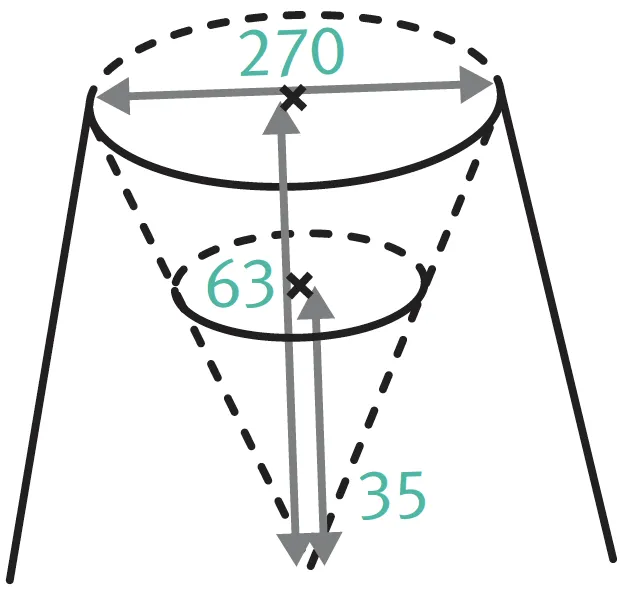
Un cratère de volcan a la forme d'un cône au fond duquel s'est formée une couche de sédiments de 35 m d'épaisseur. Le reste du cratère est à l'air libre. L'ouverture du volcan et la couche de sédiments sont considérées comme des disques parallèles.
Déterminez le volume de sédiments.
Aide
Bien quʼun schéma de la situation soit déjà proposé, nʼhésitez pas à le redessiner au brouillon pour vous lʼapproprier, vérifi er que vous lʼavez bien compris et que toutes les données du problème y sont consignées.
Déterminez le volume de sédiments.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1
Lorsque lʼon cherche le volume d'un solide formé par la section d'un autre solide, la méthode la plus simple est souvent d'appliquer les propriétés de la réduction.
Corrigé 1
- La couche de sédiments est une réduction du cône formé par le cratère du volcan. Il faut d'abord en calculer le coefficient de réduction.
Les hauteurs de ces cônes sont de 35 m et 63 m. Le coefficient de réduction est donc \dfrac{35}{63} - Le cratère en lui même a un volume de :
\dfrac{\pi r^2 \times h}{3} = \dfrac{\pi}{3} \times \left(\dfrac{270}{2}\right)^2 \times 63 \approx 1\:201\:756
Le volume du cratère est de 1 201 756 m3. - Pour obtenir le volume de sédiments, il suffit de multiplier le volume du cratère par le coefficient de réduction au cube, soit :
1\:201\:756 \times \left(\dfrac{35}{63}\right)^3 \approx 206\:062
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2
Lorsque lʼon cherche le volume d'un solide formé par la section d'un autre solide, il est aussi possible de calculer directement les dimensions du solide dont il faut trouver le volume.
Corrigé 2
- Les bases des deux cônes sont considérées comme parallèles. On peut donc choisir deux rayons de ces surfaces, parallèles, grâce auxquels on peut appliquer le théorème de Thalès.
- Le rayon du grand disque vaut 270 \div 2 = 135.
- On cherche à présent le rayon r du petit disque.
Grâce au théorème de Thalès on peut écrire :
\dfrac{63}{35} = \dfrac{135}{r} donc r = \dfrac{135 \times 35}{63} = 75.
- Nous avons maintenant toutes les mesures nécessaires pour calculer l'aire du petit cône :
\dfrac{\pi r^2 \times h}{3} = \dfrac{\pi}{3} \times 75^2 \times 35 \approx 206\:062
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Problème similaireCorbeille à papier.

Une corbeille à papier a la forme d'une pyramide tronquée comme indiqué sur le schéma ci-contre.
1. Déterminez le facteur de réduction entre la grande et la petite pyramide.
2. Déduisez-en le volume de la corbeille à papier.
1. Déterminez le facteur de réduction entre la grande et la petite pyramide.
2. Déduisez-en le volume de la corbeille à papier.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


