✔ J'envisage plusieurs méthode de résolution
✔ Je comprends la modélisation numérique ou géométrique d'une situation

\text{ABCD} est un carré de côté \text{10~cm} et \text{AE = 2,5~cm}. Le point \text{F} est le milieu de \text{[AD]}.

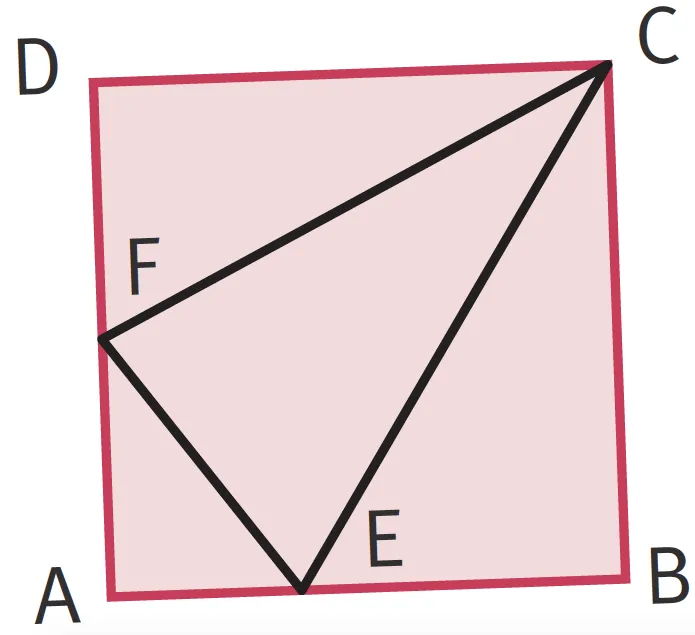Schéma géométrique : carré ABCD contenant un triangle CEF. Exercice de démonstration de propriétés géométriques.

Calculez l'aire du triangle \text{ECF}.

Afficher la correction

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 1

On détermine la longueur des trois côtés du triangle, puis on démontre que le triangle est rectangle. On en calcule alors l'aire avec la formule du triangle rectangle.

Corrigé 1

Dans le triangle \text{AEF} rectangle en \text{A}, on applique le théorème de Pythagore :

\text{EF}^2 = \text{AE}^2 + \text{AF}^2
\text{EF}^2 = 2\text{,}5^2 + 5^2 = 6\text{,}25 + 25 = 31\text{,}25
\text{EF} = \sqrt{31\text{,}25}

Dans le triangle \text{CDF} rectangle en \text{D}, on applique le théorème de Pythagore :

\text{FC}^2 = \text{DF}^2 + \text{DC}^2
\text{FC}^2 = 5^2 + 10^2 = 25 + 100 = 125
\text{FC} = \sqrt{125}

Dans le triangle \text{EBC} rectangle en \text{B}, on applique le théorème de Pythagore :

\text{EC}^2 = \text{EB}^2 + \text{BC}^2
\text{EC}^2 =7\text{,}5^2 + 10^2 = 56\text{,}25 + 100 = 156\text{,}25
\text{EC} = \sqrt{156\text{,}25}.

Le segment \text{[EF]} mesure \sqrt{31,25} \text{cm}, \text{[FC]} = \sqrt{125} \text{cm} et \text{[EC] =} \sqrt{156,25} \text{cm}.

Dans le triangle \text{ECF}, \text{[EC]} est le plus grand côté et \text{EC2}\text{ = 156,25}.

\text{CF}^2 + \text{FE}^2 = 125 + 31\text{,}25 = 156\text{,}25
On constate que \text{EC}^2 = \text{CF}^2 +\text{FE}^2.
D'après la réciproque du théorème de Pythagore, le triangle \text{ECF} est rectangle en \text{F}.

A_{\text{ECF}} = \text{FE} \times \text{FC} \div 2 = \sqrt{31\text{,}25} \times \sqrt{125} \div 2

A_{\text{ECF}} = 31\text{,}25.

L'aire du triangle \text{ECF} est égale à \text{31,25~cm}^2.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Méthode 2

Pour calculer l'aire d'une forme géométrique inscrite dans une autre forme géométrique, on calcule l'aire totale de cette dernière puis on lui enlève l'aire des formes autres que celle dont on cherche l'aire.

Corrigé 2

A_{\text{ABCD}} = 10 \times 10 = 100
L'aire du carré \text{ABCD }est égale à \text{100~cm}².
\text{AEF} est rectangle en \text{A}, \text{EBC} en \text{B} et \text{CDF} en \text{D}.

\text{AF} = 10 \div 2 = 5 \text{cm}
A_{\text{AEF}} = 2,5 \times 5 \div 2 = 6\text{,}25
Donc l'aire du triangle \text{AEF} est égale à \text{6,25}~\mathrm{cm}^{2}.
\text{EB} = 10 - 2\text{,}5 = 7\text{,}5 \text{cm}
A_{\text{EBC}} = 7\text{,}5 \times 10 \div 2 = 37\text{,}5
L'aire du triangle \text{EBC} est égale à \text{37,5}~\mathrm{cm}^{2}.
\text{DF} = 10 \div 2 = 5 \text{cm}
A_{\text{CDF}} = 5 \times 10 \div 2 = 25
L'aire du triangle \text{CDF} est égale à \text{25}~\mathrm{cm}^{2}.

A_{\text{ECF}} = 100 - (6\text{,}25 + 37\text{,}5 + 25) = 100 - 68\text{,}75
A_{\text{ECF}} = 31\text{,}25

L'aire du triangle \text{ECF} est égale à \text{31,25~cm}².

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

42
Problème similaire
Dans un trapèze

✔ Je structure mon raisonnement

Dans le trapèze \text{BCDE} suivant, les longueurs \text{BC = 6~cm} et \text{BE = 2,5~cm}.

Coup de pouce

Aire du trapèze :
A = (\text{B} + \text{b}) \times \text{h} \div 2.

Calculez l'aire de ce trapèze.

Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies

Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.

Mathématiques Cycle 4

Problèmes résolus

41Un carré

42Problème similaireDans un trapèze

Une erreur sur la page ? Une idée à proposer ?

41
Un carré

42
Problème similaire
Dans un trapèze