Nos classiques

Mathématiques Cycle 4

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Thème 1 : Nombres et calculs
Ch. 1
Arithmétique
Ch. 2
Nombres relatifs
Ch. 3
Nombres fractionnaires
Ch. 4
Calcul littéral
Ch. 5
Équations et inéquations
Ch. 6
Proportionnalité
Ch. 7
Puissances
Thème 2 : Organisation et gestion de données
Ch. 8
Statistiques
Ch. 9
Probabilités
Ch. 10
Fonctions
Thème 3 : Grandeurs et mesures
Ch. 11
Grandeurs et mesures
Thème 4 : Espace et géométrie
Ch. 12
Transformations dans le plan
Ch. 13
Triangles
Ch. 14
Angles et droites parallèles
Ch. 15
Géometrie dans l'espace
Ch. 16
Théorème de pythagore
Théorème de Pythagore
Ouverturep. 347
Je découvre le chapitre
Introductionp. 348-349
J'apprends
Coursp. 350-352
Questions Flash / Je m'entraine
Exercicesp. 353-357
Problèmes résolus
Problèmesp. 358
Problèmes résolus
Problèmesp. 359
Je résous des problèmes
Exercicesp. 360-363
Exercices numériques
Exercicesp. 364
Maths autrement : Les secrets de racine carrée de 2
Travailler autrementp. 365
Je m'évalue
Exercicesp. 366
Ch. 17
Agrandissements - réductions
Ch. 18
Trigonométrie
Annexes
Livret algorithmique et programmation
Pistes EPI
Dossier brevet
Nos dossiers d'actualité
Dossier d'actualité
Chapitre 16
Exercices

Je résous des problèmes

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

43
L'aire d'un triangle

Graphique lié à l'exercice 1
Calculez l'aire du triangle isocèle ABC.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

44
Racines carrées

Sans utiliser la calculatrice, donnez l'arrondi au dixième des racines carrées suivantes.

1. \sqrt{10}
2. \sqrt{60}
3. \sqrt{65}
4. \sqrt{90}
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

45
Départ à la pêche.

Une boite de rangement a la forme d'un cube d'arête 35 cm. Léo souhaite y placer sa canne à pêche qui mesure 55 cm.

Est-ce possible sans la plier ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

47
Rampe d'accès.

Placeholder pour Pictogramme : personne en fauteuil roulant montant une rampe d'accès.Pictogramme : personne en fauteuil roulant montant une rampe d'accès.
Une rampe d'accès pour les personnes à mobilité réduite mesure 2,50 m de long et la porte d'accès est située à 0,80 m du sol.

De quelle longueur doit-on disposer pour pouvoir poser cette rampe ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

46
Un peu de bricolage.

Schéma représentant l'étagère, l'équerre et le mur
Pour ranger ses livres, Alex pose une étagère au mur. Elle mesure 57 cm.Pour la stabiliser, il pose une équerre mesurant 1,18 m et place l'étagère à 1,15 m du sol.

L'étagère représentée ici par le segment [TA] est-elle parallèle au sol ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

48
Un triangle particulier.

Dans un triangle ABC, on sait que \text{AB} = 7 cm et que \widehat{\text{ABC}} = \widehat{\text{ACB}} = 45^{\circ}.

1. Ce triangle est-il particulier ?
2. Donnez une valeur approchée au mm de BC.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

49
Vers le Brevet (Nouvelle-Calédonie, 2009).

Le parc a la forme d'un triangle DEF. Les dimensions réelles du terrain sont DE = 12 m, EF = 9 m et DF = 15 m.

1. Pour construire ce triangle à l'échelle 1/200^{\text{e}}, complétez le tableau.

DE EF DF
Dimensions réelles (en m)
Dimensions réelles (en cm)

2. Construisez le triangle DEF à l'échelle 1/200^{\text{e}}.

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

3. Démontrez que ce terrain possède un angle droit.
4. Calculez l'aire réelle de ce parc.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

50
Des écrans d'ordinateur.

La taille d'un écran est souvent indiquée à l'aide de la longueur de sa diagonale en pouces. Calculez la diagonale des écrans suivants en pouces sachant qu'un pouce vaut 25,4 mm.

1. Largeur 42 cm, hauteur 30 cm
2. Largeur 50 cm, hauteur 35 cm
3. Largeur 22 cm, hauteur 12 cm
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

51
L'échiquier de Benoit.

Un échiquier correspond à un carré composé de 64 autres carrés de même dimension. En largeur comme en longueur, il y a 8 carrés : 4 blancs et 4 noirs alternés. L'échiquier de Benoit a une aire de 225 cm^{ 2}.

Combien mesure la diagonale d'un petit carré noir de cet échiquier ? (Arrondissez au mm.)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

52
Charlie est parti à São Paulo pour ses études.

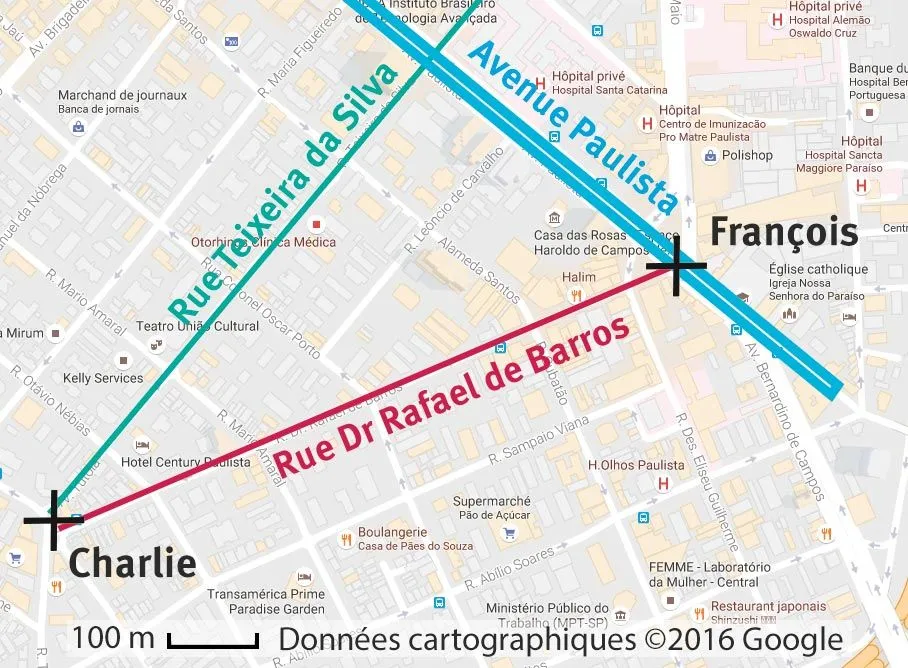
Placeholder pour Carte de São Paulo: itinéraire entre Charlie et François, rues Teixeira da Silva et Dr Rafael de Barros.Carte de São Paulo: itinéraire entre Charlie et François, rues Teixeira da Silva et Dr Rafael de Barros.
Il se trouve actuellement à l'angle de la rue Teixeira da Silva et de la rue Dr Rafael de Barros. Il doit retrouver François.La rue Dr Rafael de Barros fait 600 m. Charlie passe par la rue Teixeira da Silva qui fait 520 m et l'avenue Paulista.

Estimez la distance qu'il aurait pu parcourir en moins sachant que la rue Teixeira est perpendiculaire à l'avenue Paulista.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

53
Savoir refaire
Une histoire d'échelle.

Placeholder pour Dessin: échelle noire à deux montants contre mur beige.Dessin: échelle noire à deux montants contre mur beige.
L'écartement au sol de cette échelle est de 1,20 m.

De quelle longueur doivent être les deux jambes de l'échelle pour que son sommet soit à 1,70 m de hauteur ? (Arrondissez au cm.)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

54
Cerf-volant.

Quadrilatère ABCD, AC et DB se recoupant en O, représentant un cerf-volant.
Le cerf-volant d'Auriane est un quadrilatère dont les diagonales sont perpendiculaires. Elles mesurent 40 cm et 75 cm. Elles se coupent respectivement à leur moitié et à leur deux tiers.

Quel est le périmètre du cerf-volant d'Auriane ? (Arrondissez au cm.)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

55
Thibaud est parti skier cet hiver.

La station se trouve à 1 500 m d'altitude. L'arrivée de la télécabine qui l'amène en haut des pistes est à 2 000 m. La longueur des câbles de la télécabine est de 1 500 m.

Quelle distance Thibaud a-t-il parcourue à vol d'oiseau pour se retrouver en haut des pistes ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

56
Savoir refaire
Le créneau.

Dessin de 4 voitures, 3 vertes et une rouge, la rouge essayant de se garer entre deux vertes.
La voiture de Florian mesure 4,70 m de longueur et 1,90 m de largeur. Florian abandonne après la troisième tentative ratée de se garer en créneau dans une place de 5 m de longueur. Il s'exclame :   « Je te dis depuis le début que cette place est trop petite. » Alice répond :  « C'est juste que tu ne sais pas faire, c'est tout ! ».

Qu'en pensez-vous ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

57
Savoir refaire
Un cours de karaté.

Pendant un cours de karaté, Amandine veut améliorer ses coups de pied.Ses jambes mesurent 85 cm et elle peut les écarter de 135^{\circ} quand elle en lève une et que sa jambe d'appui est perpendiculaire au sol.
Coup de pouce
Faites un dessin et déterminez la mesure des angles. Qu'en déduisez-vous ?
À quelle hauteur peut-elle lever son pied au maximum pour donner un coup de pied ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

58
Vers la liberté.

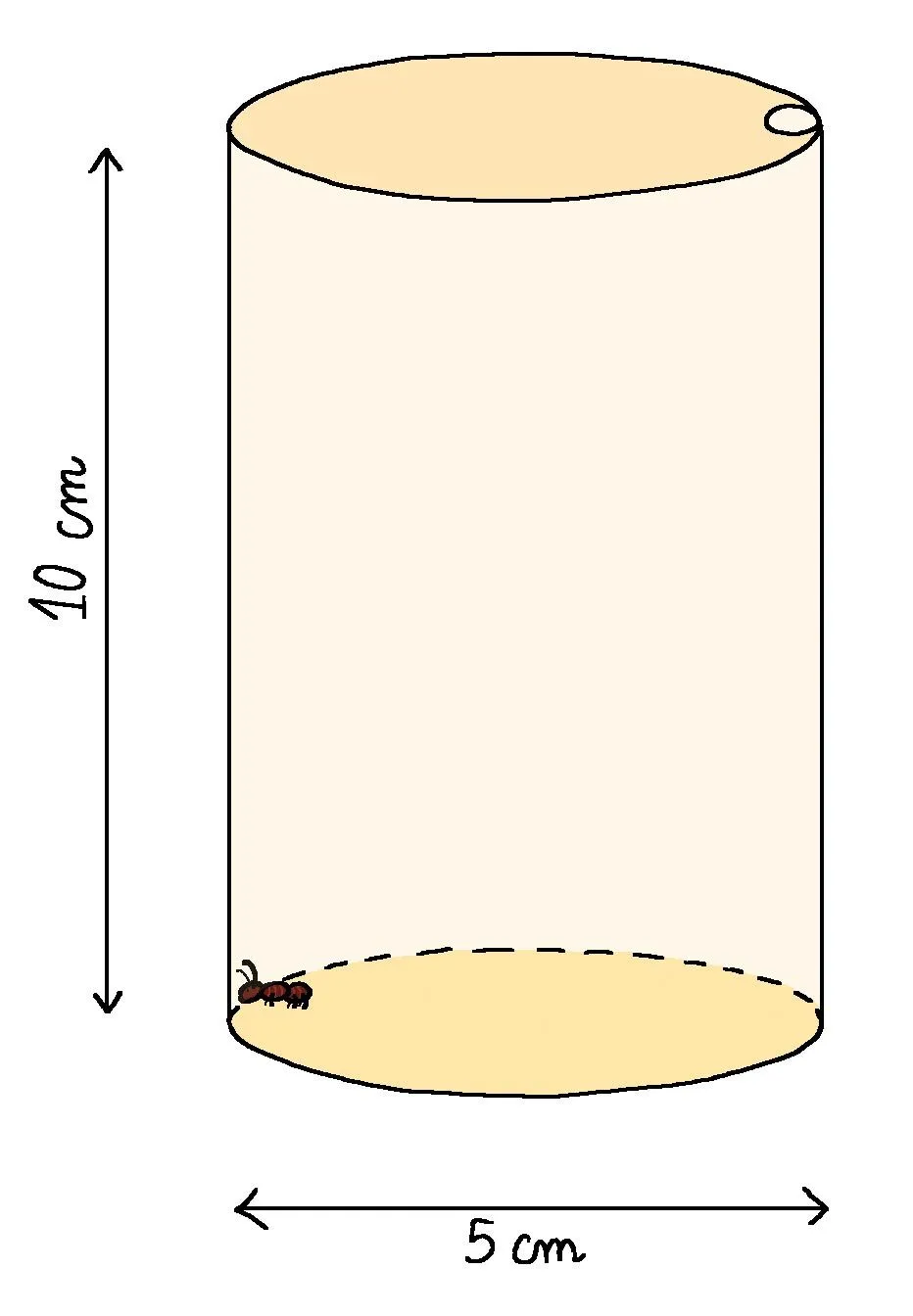
Placeholder pour Dessin: cylindre (10cm x 5cm) contenant insecte.Dessin: cylindre (10cm x 5cm) contenant insecte.
Calculez la longueur du plus court chemin qui permet à la fourmi volante enfermée dans le cylindre de recouvrer la liberté.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

59
Fabrication d'une poutre.

Représentation d'une poutre de profil carré de 20cm sur 20cm et de longueur 80cm.
On veut fabriquer une poutre d'un profil carré de côté 20 cm à partir du tronc d'un chêne.

Quel est le diamètre minimum du tronc qu'on doit utiliser ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

60
Le périmètre d'un rectangle.

Représentation d'un rectangle MNPQ, MP et NQ se croisant en O.
Un rectangle MNPQ a pour centre O. MN = 12 cm et OM = 7,5 cm.

Calculez le périmètre du rectangle MNPQ.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

62
Vers le Brevet (Centres étrangers, 2011).

Représentation des étagères
À la bibliothèque de l'école, il y a deux étagères placées dans un angle de la pièce, comme le montre le schéma.
Pour installer un ordinateur, on déplace les deux étagères d'une même distance afin de placer une table ayant la forme AEFGH comme sur le schéma ci-dessous. On précise que : BE = CF = CG = DH et que GCF est un triangle rectangle et isocèle en C.

1. Si on déplace les deux étagères de 1 m, on a CF = CG = 1 m. Combien mesure alors GF ? Donnez une valeur arrondie au cm.
2. On souhaite avoir GF = 1 m. De combien doit-on déplacer les étagères ? (Arrondissez votre réponse au cm.)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

61
Vers le Brevet (Nouvelle-Calédonie, 2013).

Représentation du mur et des point H I et S
Au lycée professionnel, Jacques et Patrick, futurs maçons, s'entrainent en construisant un mur chacun. Leur professeur, M. Eckert, vient vérifier si chaque mur est « droit », c'est-à-dire perpendiculaire au sol. Ayant oublié sa caisse à outils dans son atelier, il ne possède que le mètre ruban qu'il a dans sa poche. Pour chacun des murs, il place au pied un point I, puis un point H à 60 cm de hauteur sur le mur et un point S au sol à 80 cm de I. Il mesure ensuite la longueur HS. Pour le mur de Jacques, il trouve 1 m et, pour celui de Patrick, 95 cm.

1. Le mur de Jacques est-il droit ?
2. Et celui de Patrick ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

63
Mesures d'angles.

Dans un triangle BAC, AC = 6,8 cm, AB = 6 cm et BC = 3,2 cm.

Sachant que \widehat{\text{BAC}}=52^{\circ}, déterminez la mesure de \widehat{\text{BCA}}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

64
Un triangle à la corde

Placeholder pour Photographie d'un artisan dessinant un triangle sur un plancher en bois avec des outils anciens.Photographie d'un artisan dessinant un triangle sur un plancher en bois avec des outils anciens.
La corde à treize nœuds est un outil des bâtisseurs du Moyen Âge. Les treize nœuds définissent 12 intervalles de même longueur.

Comment permettait-elle de former un triangle rectangle ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

65
Aménagement du jardin.

Trapèze rectangle
Mon jardin a la forme d'un trapèze rectangle. AB = 16 m, CD = 36 m et BE = 34 m.

1. Sachant qu'un mètre de clôture coute 8 €, quel sera le cout de cette clôture ?
2. Sachant que le sac de pelouse permet de recouvrir 5 m^{2} et qu'il coute 7 €, donnez une valeur approchée du prix de la pelouse.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

66
Escargot de Pythagore

Représentation de l'escargot de Pythagore
1. Reproduisez la figure ci-dessous dans votre cahier ou à l'aide d'un logiciel de géométrie.

Logo Geogebra

GeoGebra

Vous devez vous connecter sur GeoGebra afin de sauvegarder votre travail

2. Construisez les points G, H et I pour conclure les trois prochaines étapes de l'escargot.

3. Quelle est la valeur exacte de la longueur des segments [BC], [BD], [BE], [BF], [BG], [BH] et [BI] ?
4. Quel est le périmètre de cette figure ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

67
Vers le Brevet (Polynésie, 2015).

Représentation schématique de l'escalier de Léa.
Léa souhaite réaliser un escalier pour monter à l'étage de son appartement. Elle a besoin pour cela de connaitre les dimensions du limon (planche dans laquelle viendront se fixer les marches de cet escalier). Elle réalise un croquis. Sur ce croquis :
  • Le limon est représenté par le quadrilatère ACDE ;
  • Les droites (AC) et (ED) sont parallèles ;
  • Les points E, A et B sont alignés ;
  • Les points B, C et D sont alignés.

Calculez ED.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Tâche complexe
Tempête.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Énoncé

Sur un petit habitable, la vitesse dépend de la taille des voiles et du vent. On réduit la taille des voiles lorsque le vent dépasse certains seuils.

Si le vent souffle à 50 km/h, quelle est l'aire de la voilure ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

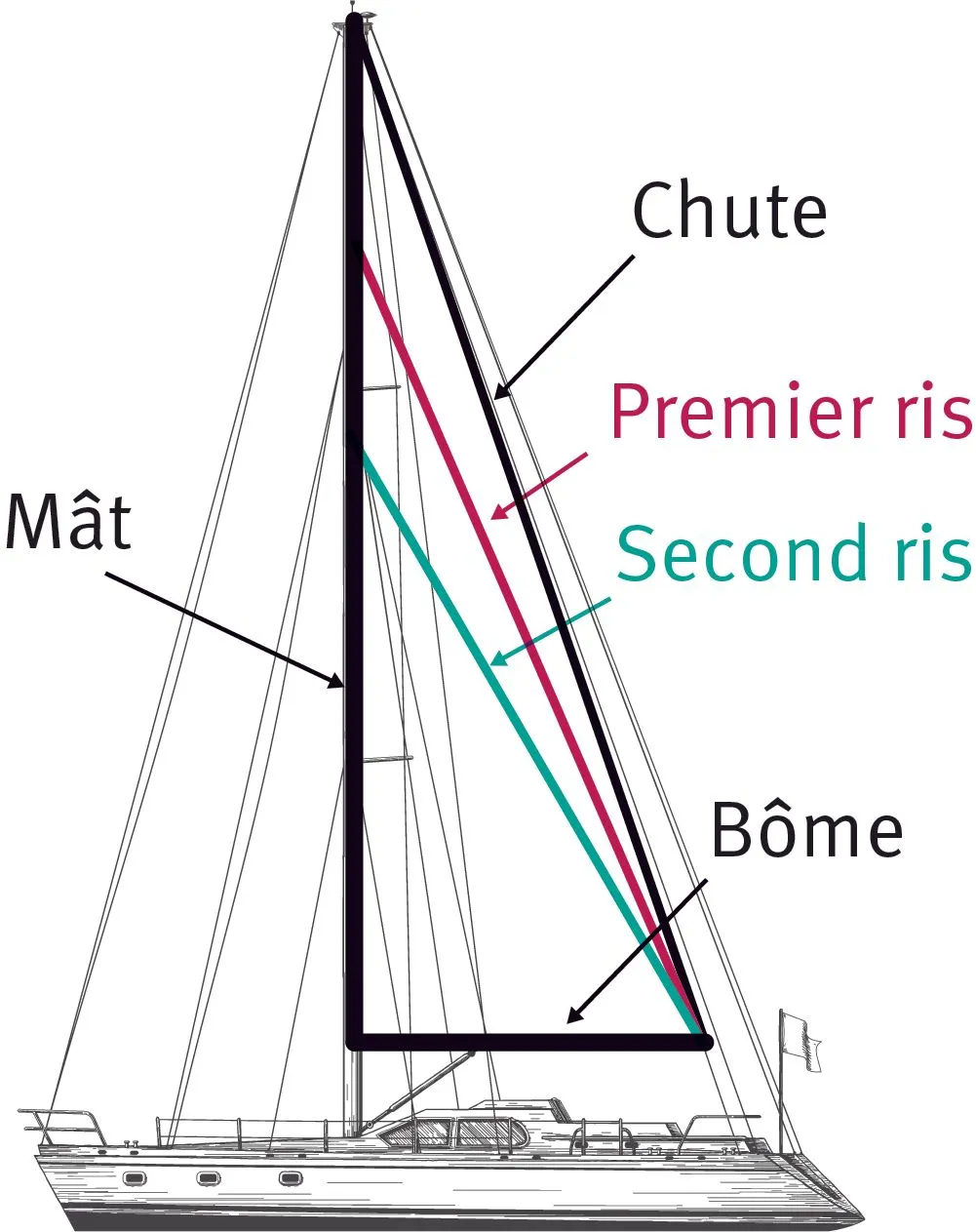
Doc. 1
Prise de ris.

Quand il y a trop de vent, on peut mettre un ris ou deux ris. La grand-voile est assimilée à un triangle rectangle.
Placeholder pour Schéma voile de bateau: mât, chute, premier ris, second ris et bôme sont indiqués.Schéma voile de bateau: mât, chute, premier ris, second ris et bôme sont indiqués.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 2
Extrait du manuel dʼutilisation.

Le premier ris diminue la chute de la voile de 80 cm. Il est utilisé quand il y a plus de 20 nœuds de vent. Le second ris diminue d'un mètre la chute de la voile que l'on a avec le premier ris. On le met quand le vent souff le a plus de 25 nœuds.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Doc. 3
Mile nautique.

En navigation, on mesure les vitesses en nœuds.
  • 1 nœud est égal à 1 mile marin/heure.
  • 1 mile marin = 1 852 m.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.