Chapitre 11
Exercices
Je résous des problèmes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48Une partie de football.
Un terrain de foot est de forme rectangulaire, de dimensions 105 m × 70 m.
1. Combien de feuilles A4 (de dimensions 21 cm × 29,7 cm) faudrait-il pour recouvrir la pelouse ?
1. Combien de feuilles A4 (de dimensions 21 cm × 29,7 cm) faudrait-il pour recouvrir la pelouse ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49Autour du Soleil.

1. Quelle distance arrondie au km près la Terre parcourt-elle en un an ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50Plan dʼun appartement.
Voici le plan dʼun appartement.
 1. Calculez la superficie de la chambre.
2. Calculez la superficie totale de lʼappartement. A-t-on besoin du résultat de la question 1 pour effectuer ce calcul ?
1. Calculez la superficie de la chambre.
2. Calculez la superficie totale de lʼappartement. A-t-on besoin du résultat de la question 1 pour effectuer ce calcul ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51Tracer.
1. Tracez sans compas trois triangles différents dont lʼaire est égale à 21\:\text{cm}^2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52Smiley.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53Pense-bête.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54Ballotins de chocolat.
Un chocolatier utilise des boites en forme de pavé droit pour vendre ses ballotins de chocolats.Le petit ballotin a un volume 1,5 fois plus petit que celui du ballotin de taille moyenne, qui représente lui-m�ême la moitié seulement du grand ballotin.
1. Sachant que le grand ballotin contient 60 chocolats, combien contiennent respectivement le moyen et le petit ballotin ?
2. Sachant que le volume du ballotin moyen est de 540 cm3, quel volume de chocolat représentent le grand et le petit ballotin ?
1. Sachant que le grand ballotin contient 60 chocolats, combien contiennent respectivement le moyen et le petit ballotin ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55Cercle et diamètre.


1. Quel diamètre peut atteindre le cercle formé à lʼaide de cette corde ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56Mile per hour.
Dans les pays anglo-saxons, lʼunité de mesure de la vitesse est le mile per hour ou mile par heure (mph). 1 mile = 1,609 kilomètres.
1. Convertissez 130 km/h en mph.
2. Une voiture américaine roulant en France à 80 mph sur autoroute limitée à 130 km/h respecte-t-elle la limitation ? Justifiez votre réponse.
3. Une voiture française roulant à 90 km/h sur une portion de route limitée à 60 mph aux États-Unis respecte-t-elle les limitations de vitesse ? Justifiez votre réponse.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57Laitons.
Le laiton est un alliage de cuivre et de zinc. La masse volumique du cuivre est de 8\text{,}920 \text{g}/\text{cm}^3 et celle du zinc de 7\text{,}150 \text{g}/\text{cm}^3.
1. Déterminez les masses volumiques des alliages suivants et complétez le tableau en arrondissant les résultats au centième.
2. Comment évolue la densité du laiton quand la proportion de zinc augmente ?
3. Combien pèse 1 \text{m}^3 de lʼalliage 1 ? De lʼalliage 2 ? De lʼalliage 3 ? De lʼalliage 4 ?
4. Convertissez ces résultats en tonnes.
1. Déterminez les masses volumiques des alliages suivants et complétez le tableau en arrondissant les résultats au centième.
| Alliage | Quantité de zinc (%) | Quantité de cuivre (%) | Masse volumique (g/cm^3) | Masse volumique (t/m^3) |
|---|---|---|---|---|
| Laiton 1 | 10 | 90 |
|
|
| Laiton 2 | 20 | 80 |
|
|
| Laiton 3 | 30 | 70 |
|
|
| Laiton 4 | 40 | 60 |
|
|
2. Comment évolue la densité du laiton quand la proportion de zinc augmente ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58Solutions chimiques et concentration.
1. Dans une solution chimique, il y a 4\text{,}72 \text{g}/\text{L} de calcium. Quelle quantité de calcium en grammes y a-t-il dans 10 L de cette solution ? Dans 100 L ? Dans 1 000 L ? Dans 1 m3 ?
2. Dans 15 L dʼune solution chimique, il y a 21 g de sodium. Quelle est la concentration de la solution en g/L ? En g/dm^3 ? En g/m^3 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59Lampe torche.
On modélise une lampe torche par la superposition de trois cylindres de révolution, comme la représentation suivante.
 1. Exprimez le volume de cette lampe torche en fonction de h et de r. On factorisera le résultat par \pi r^{2} h.
1. Exprimez le volume de cette lampe torche en fonction de h et de r. On factorisera le résultat par \pi r^{2} h.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60Marteau.
On modélise un marteau par la figure suivante.
 1. Calculez son volume.
1. Calculez son volume.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62Cône de glace.
Un cornet de glace mesure 9 cm de hauteur pour 4 cm de diamètre. Il est rempli de glace vanille jusquʼaux trois quarts, le reste du cornet étant rempli de glace à la fraise.
1. Quel est le volume du cornet ?
2. Calculez le rapport entre le volume de glace à la fraise et le volume de glace à la vanille.
3. Quel volume de glace à la vanille contient le cornet ? Déduisez-en le volume de glace à la fraise.
1. Quel est le volume du cornet ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61Objets quotidiens.
Complétez le tableau suivant. Répondez aux questions quand lʼénoncé le permet.





| Il faut calculer lʼaire de la surface pour répondre. | Il faut calculer le volume pour répondre. | Ni le calcul de lʼaire de la surface ni le calcul du volume nʼest utile. | |
|---|---|---|---|
| 1. | |||
| 2. | |||
| 3. |
1.
Quelle est la contenance dʼun vase de hauteur 30 cm et dont le diamètre de lʼextrémité supérieure est 10 cm et celui de lʼextrémité inférieure est 5 cm ?


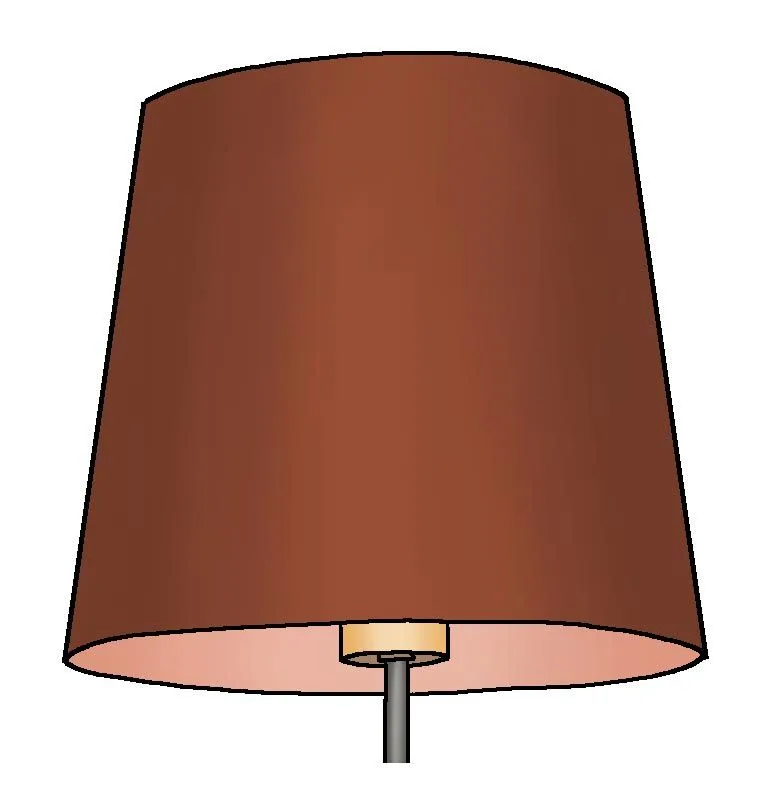
2.
Quelle surface de tissu a été utilisée pour fabriquer cette lampe ?


3.
Combien de dés de 1 cm de côté peut-on transporter dans un cône de hauteur 10 cm et rayon 2 cm ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63Vers le Brevet (Centres étrangers, 2011).

1. Quʼen pensez-vous ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64Vers le Brevet (Nouvelle-Calédonie, 2011).

1. Calculez le volume des pots de glace vanille et chocolat arrondi au \text{cm}^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65Vinaigrette.
Une vinaigrette contient trois volumes dʼhuile pour un volume de vinaigre et un volume de moutarde.
1. Quel est le pourcentage dʼhuile dans une vinaigrette ? De vinaigre ? De moutarde ?
2. Quelle quantité de chaque ingrédient exprimée en litres faut-il pour faire 50 cL de vinaigrette ?
3. Lʼunité retenue est-elle correcte pour la quantité de moutarde ? Est-elle pertinente ?
4. Sachant que la masse volumique de la moutarde est de 1\text{,}2 \text{g}/\text{cm}^3, déterminez la masse de moutarde (en grammes) nécessaire pour préparer 50 cL de vinaigrette.
1. Quel est le pourcentage dʼhuile dans une vinaigrette ? De vinaigre ? De moutarde ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66Carburants verts.
Les carburants verts sont constitués pour une partie dʼessence et, pour lʼautre, de biocarburant comme lʼéthanol. Le carburant E85 contient 15 % dʼessence et 85 % dʼéthanol.
1. Combien de litres de E85 peut-on fabriquer avec 100 \text{L} dʼéthanol ? Avec 100 \text{L} dʼessence ?
2. La mass/e volumique de lʼessence est de 0\text{,}75 \text{g}/\text{cm}^3, celle de lʼéthanol est de 0\text{,}79 \text{g}/\text{cm}^3. Quelle est la masse volumique de lʼE85 en \text{kg}/\text{m}^3 ?
3. Le sans-plomb 95 – E10 est composé de 10 % dʼéthanol et le reste dʼessence. Quelle est sa masse volumique ?
1. Combien de litres de E85 peut-on fabriquer avec 100 \text{L} dʼéthanol ? Avec 100 \text{L} dʼessence ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67Vers le Brevet (Nouvelle-Calédonie, 2011).
Une entreprise doit construire des plots en béton pour border des trottoirs. Ces plots sont formés dʼun cylindre de révolution surmonté dʼune demi-boule. La hauteur du cylindre doit être de 40 cm et son rayon de 20 cm. La demi-boule a le même rayon.
1. Calculez les volumes du cylindre et de la demi-boule arrondis au \text{cm}^3.
2. Calculez le volume de béton nécessaire pour fabriquer 1 000 plots. Donnez la réponse en \text{m}^3.
1. Calculez les volumes du cylindre et de la demi-boule arrondis au \text{cm}^3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69Construction dʼune table.

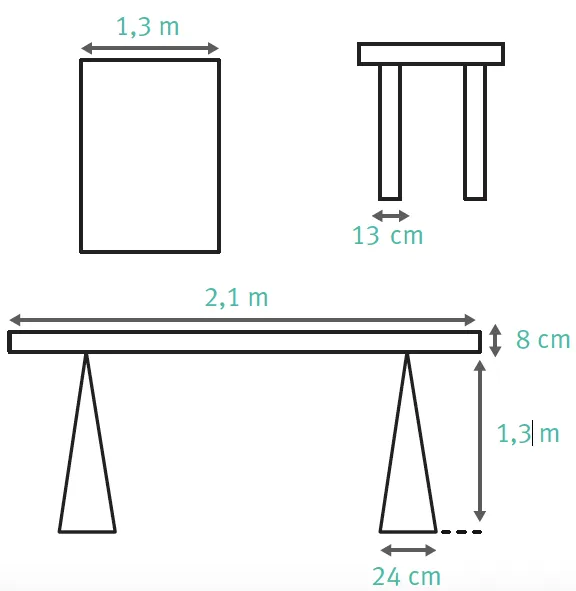
1. Calculez le volume de bois nécessaire à la confection de cette table.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68Mesure du degré dʼalcool.
1. Recherchez la masse volumique de lʼeau et exprimez-la en kg/L.
2. La masse volumique de lʼéthanol est de 7\text{,}89 \times 10^{-1} \text{kg}/\text{L}. Un litre dʼalcool est-il plus léger quʼun litre dʼeau ?
3. On plonge un bâton en forme de parallélépipède rectangle de dimensions 10 \times~10 \times 60\:\text{mm} dans la solution. Sa masse volumique est de 7 \times 10^{-1} \text{kg}/\:\text{dm}^3. Quelle est la masse de ce bâton ?
4. Le bâton est immergé dʼune hauteur h dans le liquide. Quel est le volume que prend cette partie immergée en fonction de h ? À quelle masse de liquide cela correspond-il ?
5. Pour que le bâton flotte, il faut que la masse de liquide soit égale à la masse du bâton (cʼest le principe de la poussée dʼArchimède). Trouvez cette hauteur h en fonction de x.
6. Comment, à partir de ce résultat, peut-on imaginer un système de mesure du degré dʼalcool x ?
3. On plonge un bâton en forme de parallélépipède rectangle de dimensions 10 \times~10 \times 60\:\text{mm} dans la solution. Sa masse volumique est de 7 \times 10^{-1} \text{kg}/\:\text{dm}^3. Quelle est la masse de ce bâton ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70La goutte dʼeau.


1. Le verre va-t-il déborder ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71Morceau de fromage.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72Le bon verre.
1. Parmi les verres suivants, lequel vous semble le plus adapté pour servir un jus de 40 cL ?

1. Verre pavé

2. Verre à base triangulaire

3. Verre cylindrique

4. Verre cylindrique
2. À quelle hauteur le verre que vous avez choisi sera-t-il rempli ?

1. Verre pavé

2. Verre à base triangulaire

3. Verre cylindrique

4. Verre cylindrique
2. À quelle hauteur le verre que vous avez choisi sera-t-il rempli ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73À la piscine.

1. Exprimez le volume dʼeau contenu dans la piscine comme différence entre le volume dʼun parallélépipède rectangle et celui dʼun prisme droit.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74Pyramide régulière à base carrée et cône.

- La base de la pyramide \text{SABCD} est un carré de 6 cm de côté.
- La hauteur des faces latérales de \text{SABCD} mesure 5 cm.
- Le rayon du cône mesure 3 cm.
- La pyramide et le cône ont le même volume.
1. Déterminez la hauteur \text{SO} de la pyramide.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75Pyramide.
La pyramide suivante de petits cubes comporte 5 étages. Le volume dʼun petit cube est de 1\:\text{cm}^3.
 1. Calculez le volume dʼune telle pyramide si elle comporte 10 étages.
2. À lʼaide de la formule du cours, calculez le volume de la pyramide ci-dessous.
1. Calculez le volume dʼune telle pyramide si elle comporte 10 étages.
2. À lʼaide de la formule du cours, calculez le volume de la pyramide ci-dessous.
 3. Comparez les résultats des questions 1. et 2. . Quʼen pensez-vous ?
3. Comparez les résultats des questions 1. et 2. . Quʼen pensez-vous ?


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76Prisme droit et cube.
1. Calculez le volume et lʼaire de la surface de ce prisme droit.
 2. Calculez le volume et lʼaire de la surface de
ce cube.
2. Calculez le volume et lʼaire de la surface de
ce cube.
 3. Expliquez sans calcul pourquoi les deux volumes sont égaux mais les aires de leurs surfaces sont différentes.
3. Expliquez sans calcul pourquoi les deux volumes sont égaux mais les aires de leurs surfaces sont différentes.
Aide
La surface dʼun volume est lʼaire de son patron.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77Crayon.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78Rotation et volume.


1. Quel est le volume du solide obtenu ?
Coup de pouce
Le solide obtenu correspond à la combinaison de deux solides connus opposés par leur base.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79Travaux sur le toit.
Un couvreur doit commander des tuiles qui mesurent 20 cm de largeur et 35 cm de longueur pour refaire un toit à quatre versants. Voici un schéma du toit.
 1. Estimez combien de tuiles il faudra commander pour couvrir le toit entièrement.
2. Expliquez pourquoi il sʼagit seulement dʼune estimation.
1. Estimez combien de tuiles il faudra commander pour couvrir le toit entièrement.
2. Expliquez pourquoi il sʼagit seulement dʼune estimation.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
80Trapèze et volume.
On fait tourner le trapèze \text{ABCD} autour de lʼaxe \text{(CD)}. \text{AB = 30 cm}.
 1. Décrivez lʼobjet que lʼon obtient.
2. Calculez son volume.
1. Décrivez lʼobjet que lʼon obtient.
2. Calculez son volume.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
81Vers le Brevet (Amérique du Nord, 2011).
On a empilé et collé 6 cubes de 4 cm dʼarête et un prisme droit de façon à obtenir le solide représenté suivant.La hauteur du prisme est égale à la moitié de lʼarête des cubes.

 1. /b> On nomme ce prisme \text{ABCDEF}, comme sur la figure ci-dessus. Quelle est la nature de la base de ce prisme droit ? Justifiez la réponse.
2. Vérifiez, par des calculs, que la longueur \text{AC} = 4 \sqrt{2} cm.
3. Déduisez-en la valeur exacte de lʼaire de la face \text{ACDF}. Donnez lʼarrondi au mm^2 près.
1. /b> On nomme ce prisme \text{ABCDEF}, comme sur la figure ci-dessus. Quelle est la nature de la base de ce prisme droit ? Justifiez la réponse.
2. Vérifiez, par des calculs, que la longueur \text{AC} = 4 \sqrt{2} cm.
3. Déduisez-en la valeur exacte de lʼaire de la face \text{ACDF}. Donnez lʼarrondi au mm^2 près.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
82Un verre dʼeau fraiche.

1. Quel volume dʼeau a-t-on servi ? Exprimez-le en cm^3 puis en cL.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
83Remplissage dʼune écluse.
Le débit moyen q dʼun fluide dépend de la vitesse moyenne v du fluide et de lʼaire S de lʼespace par lequel il sʼécoule. ll est donné par la formule suivante : q = S \times v où q est exprimé en \text{m}^3/\text{s} ; S est exprimé en \text{m}^2 ; v est exprimé en \text{m}/\text{s}. On considèrera que la vitesse moyenne dʼécoulement de lʼeau à travers la vanne dʼune écluse durant le remplissage est v = 2\text{,}8 m/s. La vanne a la forme dʼun disque de rayon \text{R} =~30 cm.
1. Quelle est lʼaire exacte, en m^2, de la vanne dʼune écluse ?
2. Déterminez le débit moyen arrondi au millième de cette vanne durant le remplissage.
3. Pendant combien de secondes faudra-t-il patienter pour le remplissage dʼune écluse de capacité 756 m^3 ? Est-ce quʼon attendra plus de 15 minutes ?
1. Quelle est lʼaire exacte, en m^2, de la vanne dʼune écluse ?
Coup de pouce
Aire du disque =\pi \times r^{2}.
2. Déterminez le débit moyen arrondi au millième de cette vanne durant le remplissage.
Coup de pouce
Utilisez la formule donnée dans lʼénoncé.
3. Pendant combien de secondes faudra-t-il patienter pour le remplissage dʼune écluse de capacité 756 m^3 ? Est-ce quʼon attendra plus de 15 minutes ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
84Essuie-tout.

1. Sachant que lʼépaisseur totale de papier est de 2,5 cm, calculez le volume de papier contenu dans ce rouleau.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
85Abat-jour.
Théo veut construire un abat-jour. Il a dessiné la figure suivante sur un tissu.
 1. Recopiez cette figure à lʼéchelle 1/5e et colorez la partie que Théo veut utiliser pour son abat-jour.
1. Recopiez cette figure à lʼéchelle 1/5e et colorez la partie que Théo veut utiliser pour son abat-jour.
2. Quelle surface de tissu va-t-il découper ?

Cliquez pour accéder à une zone de dessin
2. Quelle surface de tissu va-t-il découper ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
86Patron et aire.
Voici le patron dʼun cône formé par un disque de rayon r et par un secteur de cercle dʼangle \text{α} et de rayon R.

Base du cône
 1. Complétez le tableau suivant, sachant que lʼon appelle « aire du cône » lʼaire des figures qui forment son patron.
1. Complétez le tableau suivant, sachant que lʼon appelle « aire du cône » lʼaire des figures qui forment son patron.

Base du cône

| r | \alpha | R | Airecône |
|---|---|---|---|
|
| 90° | 8 dm |
|
| 12 cm | 108° |
|
|
| 10 m |
| 12 m |
|
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
87Ballon météorologique.
Des scientifiques gonflent un ballon météorologique sphérique dʼun rayon dʼun mètre avec de lʼhélium.On suppose que la température à lʼintérieur de ce ballon reste constante.La loi des gaz parfaits implique que le produit entre la pression P à la surface de ce ballon et le volume V de ce ballon reste constant.On a donc une égalité de la forme PV = a.
1. Donnez le volume de ce ballon lorsquʼil est lancé au sol.
2. Lorsque le ballon monte dans lʼatmosphère la pression diminue. Comment évolue alors le volume du ballon ? Celui-ci se gonfle-t-il ou se dégonfle-t-il ?
3. Lʼélasticité du ballon lui permet de doubler de rayon avant dʼéclater. Calculez le volume du ballon au moment où celui-ci éclate.
4. Le but des scientifiques est dʼutiliser ce ballon pour étudier lʼatmosphère à 11 000 m dʼaltitude. À cette altitude, la pression nʼest que le quart de celle de la surface de la Terre. Le ballon pourra-t-il arriver à cette altitude ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
A Exercice numérique
Les villes de Paris et Shanghaï sont distantes de 9 257 km.
Julien part de Paris à 2 h 38 et arrive à Shanghaï à 23 h 43.
1. Sachant que les heures données sont les heures locales et qu'il y a 7 heures de décalage horaire entre ces deux villes, déterminer la vitesse de l'avion qu'il a pris.
1. Sachant que les heures données sont les heures locales et qu'il y a 7 heures de décalage horaire entre ces deux villes, déterminer la vitesse de l'avion qu'il a pris.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
B Exercice numérique
Pour tester toutes les possibilités d'un code composé de 3 chiffres puis de 2 lettres, il faut 125 jours, 4 heures, 26 minutes et 40 secondes.
1. Donner le temps nécessaire pour tester une seule combinaison.
1. Donner le temps nécessaire pour tester une seule combinaison.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Tâche complexeUne arnaque ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Au IIIe siècle av. J.-C., le roi Hiéron II de Syracuse commande une couronne à un orfèvre et lui donne pour cela 2 kg dʼor. Une fois son ornement fabriqué, le roi en vérifie la masse : 2 kg. Ayant des doutes sur lʼhonnêteté de lʼartisan, il demande à Archimède de vérifier que sa couronne est faite exclusivement dʼor.
1. Que va répondre Archimède ? Lʼorfèvre a-t-il trompé le roi ? Si oui, quelle masse dʼor a-t-il subtilisée ?
1. Que va répondre Archimède ? Lʼorfèvre a-t-il trompé le roi ? Si oui, quelle masse dʼor a-t-il subtilisée ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 1La masse de lʼargent.
Lʼargent est moins dense que lʼor.
- La masse volumique de lʼargent est de 10,5 g/cm3.
- La masse volumique de lʼor est de 19,3 g/cm3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Doc. 2Lʼexpérience.
On remplit une bassine cylindrique dont
le diamètre de la base mesurait 24 cm avec 5 L dʼeau.


Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

