Chapitre 4
Activité
Fréquences conditionnelles et probabilités conditionnelles
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Compléter un tableau à double entrée à partir des fréquences marginales et conditionnelles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
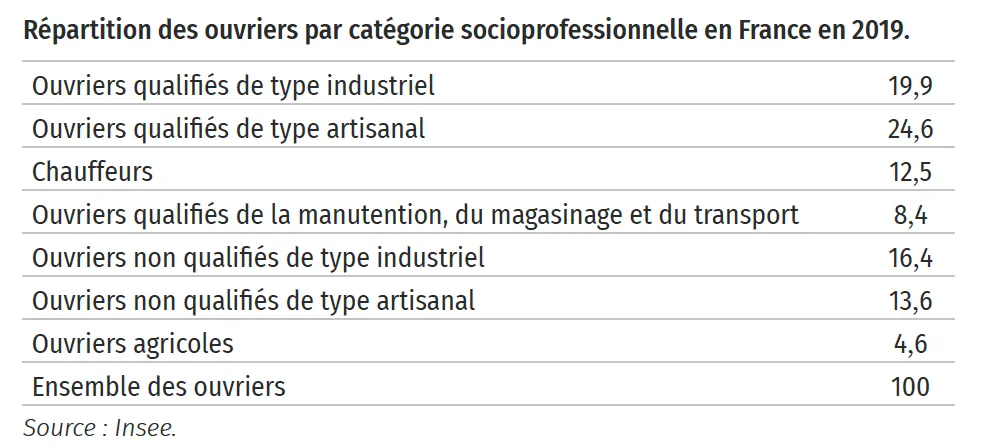
On souhaite construire un tableau représentant la répartition des ouvriers en France en 2019 par catégorie socioprofessionnelle et par sexe à partir des données précédentes en pourcentage.


1. Laquelle des affirmations suivantes est juste ? Cocher la bonne réponse.
Expliquer la différence entre ces deux affirmations.
2. Interpréter le nombre 12,5 qui apparaît dans la troisième ligne du second tableau.
3. À partir de ces tableaux, déterminer la proportion de femmes chauffeurs parmi l'ensemble des ouvriers, en pourcentage, arrondie à 0,1 % près.



Aide
Dans ce tableau, les données
sont en pourcentage, relativement à l'ensemble des ouvriers en France en 2019.
1. Laquelle des affirmations suivantes est juste ? Cocher la bonne réponse.
Expliquer la différence entre ces deux affirmations.
2. Interpréter le nombre 12,5 qui apparaît dans la troisième ligne du second tableau.
3. À partir de ces tableaux, déterminer la proportion de femmes chauffeurs parmi l'ensemble des ouvriers, en pourcentage, arrondie à 0,1 % près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'aide des tableaux exposés dans cette activité, compléter le tableau ci‑dessous avec des pourcentages calculés par rapport à l'ensemble des ouvriers de France. On arrondira au besoin les résultats à 0,1 %.
| Qualifiés, de type industriel | Qualifiés, de type artisanal | Chauffeurs | Qualifiés, de manutention | Non qualifiés, de type industriel | Non qualifiés, de type artisanal | Ouvriers agricoles | Total | |
|---|---|---|---|---|---|---|---|---|
| Femmes | ||||||||
| Hommes | ||||||||
| Total |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculer des fréquences marginales et des fréquences conditionnelles.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Le tableau ci‑dessous donne, en millier de logements, la répartition des résidences principales en France selon le nombre d'habitants et le statut d'occupation.

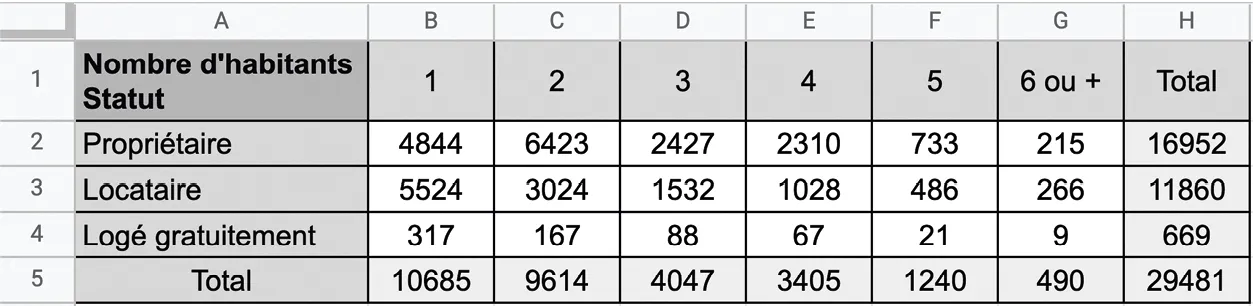
Lecture : 16 952 logements sont occupés par leur propriétaire, et, parmi ces logements, 4 844 sont occupés par leur propriétaire seul. On donnera les résultats sous forme décimale, arrondis au centième.
1. Calculer la fréquence de logements occupés par une seule personne parmi l'ensemble des résidences principales.
2. Calculer les fréquences marginales des trois statuts d'occupation, c'est‑à‑dire la proportion de logements de chaque statut (propriétaire/locataire/logé gratuitement) parmi l'ensemble des résidences principales.
4. Calculer la fréquence conditionnelle des logements habités par quatre personnes parmi les logements loués.


Lecture : 16 952 logements sont occupés par leur propriétaire, et, parmi ces logements, 4 844 sont occupés par leur propriétaire seul. On donnera les résultats sous forme décimale, arrondis au centième.
1. Calculer la fréquence de logements occupés par une seule personne parmi l'ensemble des résidences principales.
2. Calculer les fréquences marginales des trois statuts d'occupation, c'est‑à‑dire la proportion de logements de chaque statut (propriétaire/locataire/logé gratuitement) parmi l'ensemble des résidences principales.
3. Dans cette question, on s'intéresse uniquement aux logements habités par leur propriétaire. Quelle est la fréquence de logements habités par une seule personne ?
Remarque
Il s'agit d'une fréquence conditionnelle.
4. Calculer la fréquence conditionnelle des logements habités par quatre personnes parmi les logements loués.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Sur tableur, quelle est la différence entre une fréquence marginale et une fréquence conditionnelle ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
C
Black‑jack
p. 97.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Évaluer des probabilités à partir des résultats d'une simulation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
| Résultat du croupier | Première carte inférieure à 7 | Première carte supérieure ou égale à 7 |
|---|---|---|
| Total supérieur ou égal à 15 | 91 | 216 |
| Total inférieur à 15 | 116 | 77 |
Au Black‑jack, le joueur doit obtenir, en additionnant les nombres inscrits sur ses cartes, un score strictement supérieur à celui du croupier, mais sans dépasser 21. Le croupier montre sa première carte et en donne deux au joueur, qui peut alors en demander une troisième, sachant que le croupier va en ajouter une ou deux à sa main.
On suppose que le joueur totalise 15 points avec ses deux premières cartes et on cherche à savoir s'il a intérêt à demander une troisième carte, en fonction de la valeur de la première carte du croupier. Pour cela, on simule 500 parties où le croupier tire une troisième carte s'il a moins de 12 points avec les deux premières.
1. Expliquer pourquoi ces résultats permettent d'estimer que le croupier a environ 61 % de chances de faire un score total supérieur ou égal à 15.
2. Combien de fois la valeur de la première carte du croupier a‑t‑elle été inférieure à 7 ?
3. Parmi les fois où la valeur de sa première carte était inférieure à 7, combien de fois a‑t‑il obtenu 15 ou plus ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Sachant que la valeur de la première carte du croupier est inférieure à 7, quelle est la probabilité qu'il fasse un score supérieur ou égal à 15 ? Le joueur doit‑il demander une troisième carte ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille

