Synthèse

Dans un BTS, on compte 730 étudiants inscrits, dont 180 en alternance. 80 % des étudiants en alternance et 82 % des étudiants en apprentissage continu ont obtenu leur diplôme.
Dans un autre BTS, on compte 240 élèves inscrits, dont 180 en alternance. 90 % des élèves en alternance et 95 % des élèves en apprentissage continu ont obtenu leur diplôme.

1. Dans le premier BTS, combien d'élèves en alternance ont réussi leur diplôme ? Combien sont en apprentissage continu et ont obtenu le diplôme ? Comparer avec les résultats obtenus dans le second BTS.

2. Compléter le tableau d'effectifs suivant, rassemblant les résultats des deux BTS.

	Alternance	Continu	Total
Réussite
Échec
Total			970

a. On choisit un élève au hasard parmi les élèves en alternance. Quelle est la probabilité qu'il ait obtenu son diplôme ?

b. Peut‑on dire que la probabilité qu'un élève ait réussi son diplôme est plus grande parmi les élèves en formation continue ?

Pour améliorer un correcteur orthographique, un logiciel analyse les apparitions d'un mot dans un grand nombre de textes. Par exemple, sur 600 apparitions du mot « table », on compte les fois où il est précédé de « la » ou « une » et suivi d'un verbe.


1. Quelle est la probabilité que le mot « table » soit précédé du mot « la » et suivi d'un verbe ?

2. Sachant que le mot « table » est précédé de « une », quelle est la probabilité qu'il soit suivi d'un verbe ?

3. Compléter le tableau de fréquences suivant.

	« la »	« une »	Autre	Total
Verbe
Autre
Total				1

4. Quelle est la probabilité que le mot « table » ne soit précédé ni de « la » ni de « une » ?

Télécharger la

feuille de calcul

.
Cette feuille présente la répartition des étudiants français en 2015 selon le milieu d'origine, en millier d'étudiants.

1. Quelle formule doit-on entrer en H3 pour calculer, par recopie vers le bas, la fréquence d'étudiants issus d'un milieu favorisé parmi chaque formation ?
Où doit‑on ajouter un symbole \color{purple}\bf{\$} afin d'obtenir, par recopie vers la droite, les fréquences d'étudiants issus de milieux défavorisés pour chaque formation ?

Compléter le tableau 2 et afficher les résultats en pourcentage, arrondis à l'unité.

2. D'après le tableau 2, quel est le pourcentage d'étudiants issus de milieux favorisés parmi les étudiants en STS ?

3. Compléter la ligne « Total » du tableau 1.
a. Quelle formule doit‑on entrer en B13 pour obtenir, par recopie vers la droite, la fréquence d'étudiants en université relativement au milieu d'origine ?

b. Où doit-on ajouter un symbole \color{purple}\bf{\$} afin de compléter le tableau 3 par recopie vers le bas ?

4. On choisit au hasard un étudiant venant d'un milieu défavorisé. Quelle est la probabilité qu'il suive une formation STS ? Qu'il soit à l'université ?

Source des données : Insee.

On teste un test de dépistage d'un virus sur 1 000 personnes, dont 96 % sont saines et 4 % sont porteuses du virus.
Parmi les personnes saines, le test est négatif dans 97,5 % des cas. On parle dans ce cas de spécificité du test.
Parmi les porteurs du virus, le test est positif dans 95 % des cas. On parle alors de sensibilité du test.


1. Compléter le tableau suivant.



2. Quelle est la probabilité que la personne soit porteuse du virus sachant que le test est positif ?

3. Quelle est la probabilité que la personne soit saine sachant que le test est négatif ?

Un annonceur recense les médias les plus utilisés selon l'âge des utilisateurs afin de cibler les publicités proposées, en millier de personnes.


On choisit une personne au hasard.

1. Quelle est la probabilité que son média favori soit la télévision et qu'elle ait moins de 18 ans ?

2. Sachant que la personne choisie a moins de 18 ans, quelle est la probabilité que son média favori soit la presse ?

3. 90 % des moins de 18 ans qui lisent la presse la lisent sur Internet. Combien de jeunes cela représente‑t‑il ?

4. Parmi les personnes utilisant majoritairement la radio, quelle est la fréquence des moins de 18 ans ?

5. Calculer la fréquence conditionnelle des moins de 18 ans parmi les personnes qui préfèrent la presse.

Pour tester si un magnétiseur arrive à deviner la présence d'une personne dans une pièce sans la voir, on partage la pièce en deux parties par une cloison et on lui demande 80 fois de suite s'il y a quelqu'un derrière cette dernière, en faisant entrer, ou non, de manière aléatoire une personne à chaque fois.
On note \text{M} et \text{N} les événements « Le magnétiseur répond oui. » et « Il y a quelqu'un dans la pièce. ».

Les résultats obtenus sont les suivants.


1. Compléter le tableau.

2. Calculer et interpréter \mathrm{P}(\mathrm{M} \cap \mathrm{N}) et \mathrm{P}(\overline{\mathrm{M}} \cap \overline{\mathrm{N}}).
En déduire la probabilité que le magnétiseur devine correctement.

3. Calculer et interpréter \mathrm{P}_{\mathrm{N}}(\mathrm{M}).

Télécharger la

feuille de tableur

.
Le tableur présente la répartition des jeunes selon l'activité et le sexe en 2015, en pourcentage du nombre de personnes de chaque classe d'âge.

1. Vérifier que le pourcentage total de chaque colonne est bien 100 %.

2. On souhaite compléter le tableau regroupant les hommes et les femmes. Expliquer pourquoi on ne peut pas se contenter de calculer la moyenne des hommes et des femmes pour chaque catégorie.

3. En utilisant la ligne 9, créer deux tableaux, donnant les effectifs de femmes et d'hommes par âge et par activité, puis un troisième tableau d'effectifs rassemblant les hommes et les femmes.

4. Quelle est la fréquence de personnes en études initiales parmi les 18‑20 ans ?

5. En utilisant les données obtenues, compléter le graphique ci‑dessous, montrant la répartition des jeunes dans chaque type d'activité selon l'âge, grâce à notre outil d'édition d'image.

Un adepte des paris sportifs recueille des données sur 350 matchs de son équipe favorite. Il remarque que cette équipe gagne le match 75 % des fois où elle mène à la première mi‑temps, ce qui est arrivé 200 fois, qu'il y a match nul sur 8 % des matchs qu'elle a joués. Parmi ces matchs nuls, l'équipe a mené 16 fois à la première mi‑temps. Enfin, cette équipe a gagné 60 % de ses matchs.

1. Compléter le tableau suivant.

	Gagne	Nul	Perd	Total
Mène à la 1re mi‑temps
Ne mène pas à la 1re mi‑temps
Total				350

2. A‑t‑on plus intérêt à parier sur un match nul quand cette équipe mène à la première mi-temps ou quand elle ne mène pas ? Expliquer.

3. A‑t‑on plus intérêt à parier qu'elle va perdre quand elle ne mène pas à la première mi‑temps ou qu'elle va gagner quand elle mène à la mi‑temps ?

Pour diminuer les émissions de gaz nocifs des voitures à essence, on ajoute des catalyseurs dans le pot d'échappement qui permettent de réduire ou d'oxyder ces gaz afin de les rendre inoffensifs.
Ces émissions de gaz nocifs sont constituées de deux tiers de monoxyde de carbone (\text{CO}), d'un quart d'hydrocarbures (\text{HC}) et d'un douzième d'oxydes d'azote (\text{NO}_{x}).
Lors du test d'un système de catalyseurs, on mesure que 60 % du monoxyde de carbone a été oxydé, et 50 % des hydrocarbures et 90 % de l'oxyde d'azote ont été réduits.

1. Compléter le tableau suivant pour 1,2 g d'émissions (correspondant à 1 km parcouru).

	\bf{CO}	\bf{HC}	\bf{NO}_{x}	Total
Réduit
Non réduit
Total				1,2

2. Calculer le pourcentage de gaz nocifs réduits.

3. Quelle est la fréquence d'hydrocarbures parmi les gaz nocifs non réduits ? Arrondir à 10^{-2} près.

4. Quelle est la fréquence d'oxyde d'azote parmi les gaz nocifs réduits ?

Un marchand de produits en vrac se fournit chez trois fournisseurs. Il remarque que 2 % des produits du fournisseur \text{A} sont abîmés, contre 3,5 % des produits du fournisseur \text{B} et 5 % des produits du fournisseur \text{C}. Il se demande comment répartir ses commandes pour avoir au maximum 3 % de produits abîmés en achetant le plus possible au fournisseur \text{C}.

Ouvrir une feuille de calcul et recopier le tableau ci‑dessous.



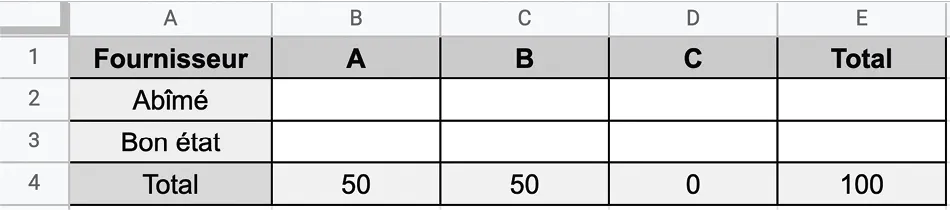
1. Quelles formules doit‑on entrer en B2, C2 et D2 pour obtenir les quantités de produits abîmés provenant respectivement des fournisseurs A, B, C ?

2. Quelle formule doit‑on entrer en B3 pour obtenir, en la glissant vers la droite, les nombres de produits en bon état provenant de chaque fournisseur ?

3. Quelle formule doit-on entrer en E2 pour obtenir, en la glissant vers le bas, les quantités de produits abîmés et en bon état dans le stock total ?

4. Entrer en B4 et en C4 la formule \color{purple}\bf{=(100-D4)/2} et saisir 50 en D4. Quelle est alors la fréquence de produits abîmés dans son stock ?

5. En supposant qu'on achète autant aux fournisseurs A et B, quelle est la plus grande quantité qu'on puisse acheter au fournisseur C de manière à avoir moins de 3 % de produits abîmés ?

Un lycée organise une sortie au cinéma. 15 % de l'équipe éducative et 65 % des élèves s'y inscrivent. Au total, c'est 60 % de l'effectif du lycée (équipe éducative et élèves rassemblés) qui s'y rend.

Quelle est la proportion d'élèves dans ce lycée ?

On met des papiers portant des nombres entiers dans une urne. Un joueur tire un papier au hasard. Il gagne si le numéro tiré est pair et multiple de 3.

Proposer une composition de l'urne telle qu'un joueur ait 75 % de chances de tirer un nombre pair, 60 % de chances de tirer un multiple de 3 mais seulement 40 % de chances de gagner.