On choisit au hasard un fonctionnaire dans une administration qui en compte 65 de catégorie A dont 15 en temps partiel et 85 de catégorie B dont 33 en temps partiel. On note \text{A} l'événement « La personne choisie est de catégorie A. », \text{B} l'événement « La personne est de catégorie B. » et \text{C} l'événement « La personne choisie travaille à temps complet. ».

1. Interpréter par une phrase l'événement \text{A} \cap \text{C}.

2. Interpréter par une phrase l'événement \overline{\text{C}}.

3. Compléter le tableau d'effectifs suivant.



4. En déduire la probabilité de l'événement \text{A} \cup \overline{\text{C}} et interpréter ce résultat.

Pour tester un médicament, on note, pour chaque patient cobaye, s'il a reçu le médicament testé ou un placebo et s'il ressent certains symptômes. On note 0 pour non et 1 pour oui.
On a résumé les résultats obtenus pour quatre patients.


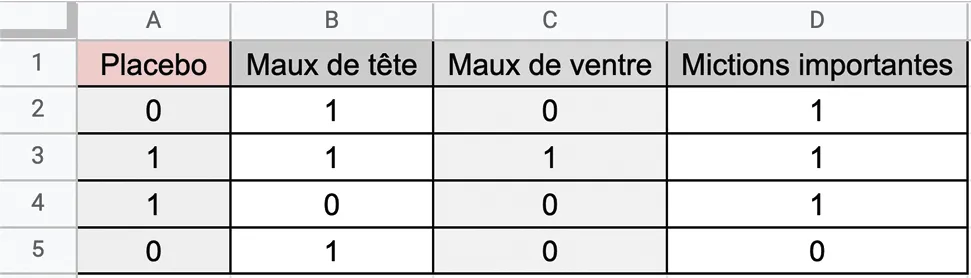
1. Proposer une formule à entrer en E2 qui affiche 1 si le patient de la ligne 2 a reçu le médicament et a des maux de tête et 0 sinon.

2. Proposer une formule à entrer en F2 qui affiche 1 si le patient de la ligne 2 a un des trois symptômes et 0 sinon.

3. Proposer une formule à entrer en G2 qui affiche 1 si le patient de la ligne 2 a reçu le placebo et n'a aucun des trois symptômes.

Lors du test d'un médicament sur 300 personnes, 80 ont reçu sans le savoir un médicament placebo. Les effets secondaires relevés sont les suivants.


On choisit au hasard un participant du test.
On note \text{A} l'événement « Le patient ressent des effets secondaires. » et \text{B} l'événement « Le patient a reçu un placebo. ».



1. Calculer les probabilités des événements \text{A} et \text{B}.

2. Calculer et interpréter \mathrm{P}(\overline{\mathrm{A}} \cap \mathrm{B}). Arrondir à 0,01 près.

3. Calculer et interpréter \mathrm{P}(\mathrm{B} \cup \mathrm{A}). Arrondir à 0,01 près.

Dans une usine de montage, 7 % des appareils sortants ont un défaut de fabrication. Dans 75 % des cas, ce défaut est visible et le produit est écarté. Certains appareils, sans défaut, sont retirés par erreur.
Sur un lot de 400 appareils, 32 sont écartés.

1. Calculer la fréquence de produits écartés.

2. Compléter le tableau suivant.



3. On choisit un appareil au hasard parmi les produits écartés. Quelle est la probabilité qu'il ait un défaut ?

4. Quelle est la probabilité qu'un produit non écarté ait malgré tout un défaut ?

Dans une ville A, 30 % des habitants n'ont pas de voiture, contre 10 % dans la ville B voisine et 16 % dans la ville C. Or les habitants de A représentent 12 % de cette agglomération, les habitants de la ville B en représentent 38 % et ceux de C en représentent 50 %.
On interroge un habitant de l'agglomération au hasard.

1. Calculer la probabilité qu'il vienne de la ville A et n'ait pas de voiture.

2. Calculer la probabilité qu'il n'ait pas de voiture.

On souhaite tester la présence d'ions sulfate dans une solution. On y verse successivement du chlorure de baryum puis du chlorure d'hydrogène.
Dans 80 % des échantillons, il se forme un précipité blanc et, dans 25 % des cas, ce précipité se dissout avec le chlorure d'hydrogène, ce qui montre qu'il n'est pas dû à des ions sulfate.
Cependant, il arrive une fois sur 100 que, malgré la présence d'ions sulfate, le précipité ne se forme pas.

1. On note respectivement \text{B} et \text{S} les événements « Il se forme un précipité blanc. » et « La solution contient des ions sulfate. ». Compléter le tableau de fréquence suivant.


2. Calculer la probabilité que la solution contienne des ions sulfate.

3. Sachant que la solution ne précipite pas, quelle est la probabilité qu'elle contienne tout de même des ions sulfate ?

Environ 26 % des étudiants français suivent leur scolarité en Île‑de‑France. 51 % des étudiants d'Île‑de‑France et 62 % des étudiants de province sont inscrits dans une université.
On choisit un étudiant français au hasard. On note \text{F} l'événement « L'étudiant choisi est inscrit en Île‑de‑France. » et \text{U} l'événement « L'étudiant choisi est inscrit dans une université. ».

1. Donner les valeurs de \mathrm{P}_{\mathrm{F}}(\mathrm{U}) et \mathrm{P}_{\overline{\mathrm{F}}}(\mathrm{U}). Justifier en citant l'énoncé.

2. Déterminer la probabilité qu'un étudiant soit inscrit en province et celle qu'un étudiant soit inscrit dans une université de province.

Un parc d'attractions a relevé les modes de transport utilisés et les distances de provenance des visiteurs.


On choisit au hasard un visiteur du parc. On note respectivement \text{V} et \text{A} les événements « Le visiteur est venu en voiture. » et « Le visiteur a parcouru moins de 100 km. ».

1. Calculer et interpréter \mathrm{P}_{\mathrm{A}}(\mathrm{V}) et \mathrm{P}_{\overline{\mathrm{A}}}(\mathrm{V}).

2. Pour réduire les émanations de gaz à effet de serre des visiteurs, on met en place des bus venant des trois grandes villes situées à moins de 100 km du parc.
a. L'impact environnemental d'un bus est donné par :

masse transportée(tonnes) \times 0,271 \times distance(km).

Si la masse moyenne d'une personne est de 65 kg, quel est l'impact environnemental sur 100 km d'un bus transportant 50 personnes ?

b. En déduire l'impact environnemental pour 865 visiteurs (soit 18 bus).

c. L'impact environnemental d'un voyage en voiture pour une personne est égal, en moyenne, à

0,065 \times 2,823 \times distance(km).

Quel est l'impact de 865 personnes parcourant 100 km en voiture ?

Un spectacle propose 1 650 places à la vente, en guichet ou sur Internet. Les places ont toutes été vendues, la semaine précédant le spectacle ou le jour même, selon le tableau suivant.


On choisit un spectateur au hasard et on note \text{A} l'événement « Le spectateur a acheté son billet dans la semaine. » et \text{G} l'événement « Le spectateur a acheté son billet au guichet. ».

1. Sachant que le spectateur choisi a acheté sur Internet, quelle est la probabilité qu'il ait acheté son billet le jour même ?

2. Calculer et interpréter \mathrm{P}_{\mathrm{A}}(\mathrm{G}).