Variables aléatoires

Définition : On considère la série statistique donnée par le tableau ci‑dessous et on note $\text{N}=n_1+n_2+\dots +n_p$ l'effectif total.
La moyenne pondérée de la série est le nombre, noté $\bar{x},$ tel que $\bar{x}=\frac{n_1{x}_1+\dots +n_p{x}_p}{\text{N}}.$


Propriété : Si on note $f_1,\dots ,f_p$ les fréquences associées aux valeurs $x_1,\dots ,x_p,$ la moyenne est donnée par $\bar{x}=x_1{f}_1+\dots +x_p{f}_p.$

Exemple :

On relève le nombre d'appels reçus chaque jour par un standardiste pendant 20 jours. La moyenne pondérée est :

Propriété : Dans une situation d'équiprobabilité, la probabilité d'un événement $\text{A}$ est :


Dans les cas simples, cela correspond à la fréquence d'apparition d'un caractère.

Exemples :
1. On lance un dé à six faces équilibré, et on note $\text{A}$ l'événement « Obtenir un nombre pair ». Les trois issues $2,$ $4$ et $6$ sont favorables à $\text{A},$ et il y a six issues au total, donc $\text{P}\left(\text{A}\right)=\frac{3}{6}=\frac{1}{2}.$

2. Le matin, Dominique choisit au hasard dans son tiroir une paire de chaussettes indiscernables au toucher dont la répartition est donnée par le diagramme en barres ci‑dessous.


La probabilité qu'elle choisisse une paire grise est $\frac{7}{28}=\frac{1}{4}.$

Définition : Soit $\text{A}$ un événement d'un univers $\Omega .$ L'événement complémentaire de $\text{A}$ est l'événement, noté $\bar{\text{A}},$ formé de toutes les issues qui ne réalisent pas $\text{A}$. Autrement dit, $\text{A}\cap \bar{\text{A}}=\varnothing$ et $\text{A}\cup \bar{\text{A}}=\Omega .$

Propriété : Pour tout événement $\text{A}$ , on a $\text{P}(\bar{\text{A}})=1-\text{P}(\text{A}).$

Exemple : À un carrefour, on a constaté que la probabilité qu'un feu soit vert est de $0,512.$ Ainsi, la probabilité que le feu ne soit pas vert est $1-0,512=0,488.$

Définitions :
1. La fonction $\mathbf{SOMME}$ calcule la somme d'une série d'une série de données. La saisie $=\mathbf{SOMME}(Case1:Case2)$ calcule la somme des valeurs contenues dans toutes les cases entre $Case1$ et $Case2$.

2. La fonction $\mathbf{SI}$ du tableur permet de remplir une case selon une condition. Pour cela, on saisit dans la case concernée $=\mathbf{SI}(\mathbf{condition};Valeur1;Valeur2)$. Dans ce cas, la case sera remplie avec la valeur $Valeur1$ si la condition est vérifiée, et $Valeur2$ sinon.

Exemple :


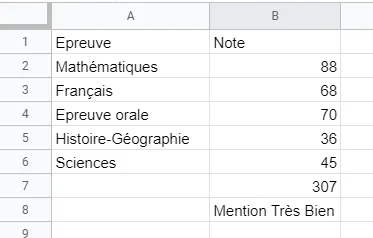
Emilie a rentré dans ce tableau ses résultats aux épreuves finales du brevet. Elle souhaite calculer sa note sur ces épreuves et savoir si elle aura la mention Très Bien (à partir de 300 points) ou la mention Bien.
Dans la case B7, elle saisit = SOMME(B2 : B6) ; dans la case B8, elle saisit = SI(B7 >= 300} ; “Mention Très Bien” ; “Mention Bien”).

1. Calculer la probabilité d'une issue ou d'une réunion d'issues dans une situation simple décrite par une phrase ou un graphique.
2. Décrire l'événement contraire d'un événement et calculer sa probabilité.
3. Calculer une valeur moyenne en utilisant les fréquences.
4. Calculer une proportion de proportion.
5. Utiliser les fonctions $\mathbf{SI}$ et $\mathbf{SOMME}$ d'un tableur.

On choisit un entier au hasard entre $1$ et $100.$

1. Quelle est la probabilité de choisir un nombre strictement inférieur à $21$ ?

2. Quel est l'événement contraire de l'événement « Choisir un nombre strictement inférieur à 9. » ?

3. Quelle est la probabilité de l'événement contraire de « Choisir 8 ou 9. » ?

Dans une feuille de calcul, que fait la formule $=\mathbf{SI}(A1=6;1;0)$ entrée dans une cellule autre que la cellule $A1$ ?

Calculer la valeur moyenne de la série suivante.

Parmi les formules ci‑dessous écrites dans la cellule $B1$ d'une feuille de calcul, identifier celles qui calculent la même somme.

1. $=\mathbf{SOMME}(A1:A4)$
2. $=A1+A4$
3. $=\mathbf{SOMME}(A1;A4)$
4. $=A1+A2+A3+A4$

On lance deux fois de suite une pièce bien équilibrée. Quelle est la probabilité d'obtenir au moins une fois la face « Pile » ?

Le chevalier de Méré (XVII^e siècle) était un joueur et souhaitait connaître les stratégies amenant à un plus grand nombre de succès. Il soumet ce problème : « Deux joueurs misent chacun 32 pistoles dans un jeu en trois manches gagnantes. La partie est interrompue alors que le premier joueur a remporté deux manches et le second une seule. Quel doit être alors le gain de chacun des deux joueurs ? » Pascal et Fermat relèvent le défi et on retrouve les réponses basées sur les probabilités dans leurs échanges épistolaires.